New In 
Wild cluster bootstrap
Do your data have a small number of clusters or an uneven number of observations per cluster? Do you want to make inferences about parameters in a linear model? With the new wildbootstrap command, you can now use wild cluster bootstrap (WCB) in these situations.
Highlights
-
Wild cluster bootstrap p-values and confidence intervals for hypothesis tests about parameters from linear regression models
-
Support for areg, regress, and xtreg, fe
-
Support for Rademacher, Mammen, Webb, gamma, and normal distributions for the error weights
-
Support for symmetric and equal-tailed p-value criteria
Overview
The WCB proposed by Cameron, Gelbach, and Miller (2008), provides an alternative to the cluster–robust variance estimator when you have either a small number of clusters or an uneven number of observations across clusters.
When we fit models with clustered observations, we often use a cluster–robust variance estimator, which relaxes the independence assumption for observations within each cluster. This estimator works well if we have many clusters and if the clusters do not differ too much in their numbers of observations. However, if this is not the case, we may obtain better estimates using the WCB.
Stata’s new wildbootstrap command estimates WCB p-values and confidence intervals (CIs) for tests of simple and composite linear hypotheses about parameters from linear regression models. These statistics can be obtained when fitting linear regression models such as those fit with regress, models with a large indicator-variable set such as those fit with areg, and fixed-effects models such as those fit with xtreg, fe.
Let’s see it work
We would like to see the effect of tenure on wages and to account for clusters at the industry level. Here we use a wage dataset from 1988 with only 12 clusters with substantially varying cluster sizes, from 4 to 817, deviating from the assumptions required for the cluster–robust variance estimator to be reliable. We fit a linear regression and compute WCB statistics for a test that the coefficient on tenure is zero. We set the seed using rseed() for reproducibility.
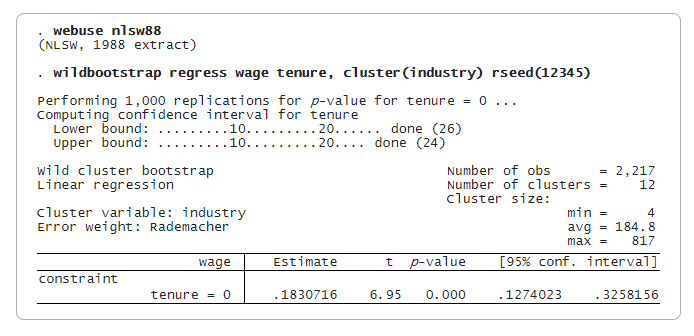
Reference
Cameron, C. A., J.B. Gelbach, and D.L. Miller. 2008. Bootstrap-based improvements for inference with clustered errors. The Review of Economics and Statistics 90: 417–427.
