Overview

Die von Cameron, Gelbach und Miller (2008) vorgeschlagene WCB bietet eine Alternative zum clusterrobusten Varianzschätzer, wenn entweder eine geringe Anzahl von Clustern oder eine ungerade Anzahl von Beobachtungen in den Clustern vorliegt.

Bei der Anpassung von Modellen mit geclusterten Beobachtungen wird häufig ein clusterrobuster Varianzschätzer verwendet, der die Unabhängigkeitsannahme für Beobachtungen innerhalb jedes Clusters lockert. Dieser Schätzer funktioniert gut, wenn wir viele Cluster haben und wenn sich die Cluster nicht zu sehr in der Anzahl der Beobachtungen unterscheiden. Wenn dies jedoch nicht der Fall ist, können wir mit dem WCB bessere Schätzungen erhalten.

Der neue wildbootstrap-Befehl von Stata schätzt WCB p-Werte und Konfidenzintervalle (CIs) für Tests von einfachen und zusammengesetzten linearen Hypothesen über Parameter aus linearen Regressionsmodellen. Diese Statistiken können bei der Anpassung von linearen Regressionsmodellen (z. B. mit regress), Modellen mit einem großen Satz von Indikatorvariablen (z. B. mit areg) und Modellen mit festen Effekten (z. B. mit xtreg, fe) ermittelt werden.

Wir wollen sehen, wie es funktioniert

Wir möchten die Auswirkungen der Betriebszugehörigkeit auf die Löhne untersuchen und Cluster auf Branchenebene berücksichtigen. Hier verwenden wir einen Lohndatensatz aus dem Jahr 1988 mit nur 12 Clustern mit stark variierenden Clustergrößen von 4 bis 817, was von den Annahmen abweicht, die erforderlich sind, damit der clusterrobuste Varianzschätzer zuverlässig ist. Wir passen eine lineare Regression an und berechnen WCB-Statistiken für einen Test, dass der Koeffizient für die Betriebszugehörigkeit Null ist. Wir setzen den Seed mit rseed(), um die Reproduzierbarkeit zu gewährleisten.

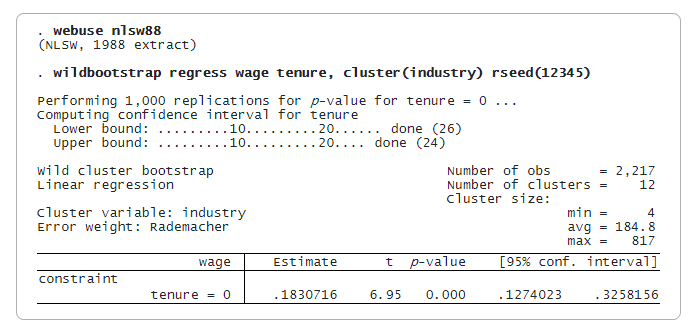
Referenz

Cameron, C. A., J.B. Gelbach, und D.L. Miller. 2008. Bootstrap-basierte Verbesserungen für Inferenzen mit geclusterten Fehlern. The Review of Economics and Statistics 90: 417-427.