Vue d’ensemble

Le WCB proposé par Cameron, Gelbach et Miller (2008) offre une alternative à l’estimateur de variance par grappes lorsque le nombre de grappes est faible ou que le nombre d’observations dans les grappes est inégal.

Lorsque nous ajustons des modèles avec des observations en grappes, nous utilisons souvent un estimateur de variance robuste en grappes, qui relâche l’hypothèse d’indépendance pour les observations au sein de chaque grappe. Cet estimateur fonctionne bien si nous avons beaucoup de grappes et si les grappes ne diffèrent pas trop dans leur nombre d’observations. Toutefois, si ce n’est pas le cas, nous pouvons obtenir de meilleures estimations en utilisant le WCB.

La nouvelle commande wildbootstrap de Stata estime les valeurs p et les intervalles de confiance (IC) du WCB pour les tests d’hypothèses linéaires simples et composites sur les paramètres des modèles de régression linéaire. Ces statistiques peuvent être obtenues lors de l’ajustement de modèles de régression linéaire tels que ceux ajustés avec regress, de modèles avec un grand ensemble de variables indicatrices tels que ceux ajustés avec areg, et de modèles à effets fixes tels que ceux ajustés avec xtreg, fe.

Voyons comment cela fonctionne

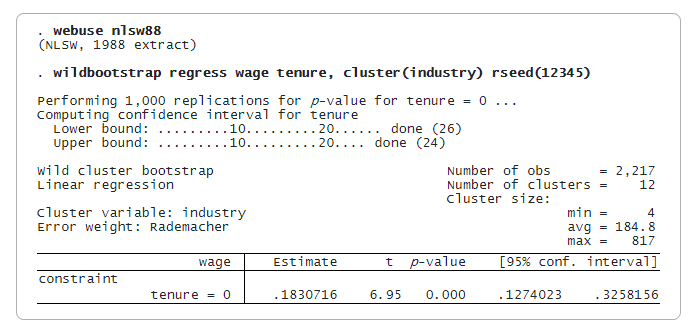
Nous aimerions voir l’effet de la durée d’occupation sur les salaires et tenir compte des grappes au niveau de l’industrie. Nous utilisons ici un ensemble de données salariales de 1988 ne comportant que 12 grappes dont la taille varie considérablement, de 4 à 817, ce qui s’écarte des hypothèses requises pour que l’estimateur de variance par grappes soit fiable. Nous ajustons une régression linéaire et calculons les statistiques WCB pour tester que le coefficient de la durée d’occupation est nul. Nous définissons la graine à l’aide de rseed() pour des raisons de reproductibilité.

Référence

Cameron, C. A., J.B. Gelbach, et D.L. Miller. 2008. Bootstrap-based improvements for inference with clustered errors. The Review of Economics and Statistics 90 : 417-427.