Áttekintés

A Cameron, Gelbach és Miller (2008) által javasolt WCB alternatívát kínál a klaszter-robosztus varianciabecslőhöz képest, ha a klaszterek száma kicsi vagy a klaszterek között egyenlőtlen számú megfigyelés van.

Amikor klaszterezett megfigyelésekkel rendelkező modelleket illesztünk, gyakran használjuk a klaszter-robosztus varianciabecslőt, amely lazítja az egyes klasztereken belüli megfigyelések függetlenségi feltételezését. Ez a becslő jól működik, ha sok klaszterünk van, és ha a klaszterek nem különböznek túlságosan a megfigyelések számában. Ha azonban ez nem így van, akkor a WCB használatával jobb becsléseket kaphatunk.

A Stata új wildbootstrap parancsa WCB p-értékeket és konfidenciaintervallumokat (CI) becsül lineáris regressziós modellek paramétereire vonatkozó egyszerű és összetett lineáris hipotézisek teszteléséhez. Ezeket a statisztikákat lineáris regressziós modellek, például a regress programmal illesztett modellek, nagy indikátor-változóhalmazzal rendelkező modellek, például az areg programmal illesztett modellek, és fix hatású modellek, például az xtreg, fe programmal illesztett modellek esetén kaphatjuk meg.

Lássuk, hogyan működik

Szeretnénk látni a munkakörök bérre gyakorolt hatását, és szeretnénk figyelembe venni a klasztereket ágazati szinten. Itt egy 1988-as béradatállományt használunk, amely csak 12 klasztert tartalmaz, a klaszterek mérete pedig jelentősen változik, 4 és 817 között, ami eltér a klaszter-robosztus varianciabecslő megbízhatóságához szükséges feltételezésektől. Lineáris regressziót alkalmazunk, és kiszámítjuk a WCB-statisztikákat annak tesztelésére, hogy a bérrel kapcsolatos együttható nulla. A reprodukálhatóság érdekében a magot az rseed() segítségével állítjuk be.

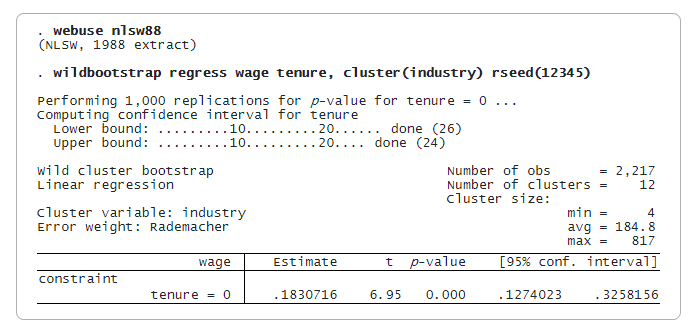
Hivatkozás

Cameron, C. A., J. B. Gelbach és D. L. Miller. 2008. Bootstrap-alapú fejlesztések klaszteres hibákkal történő következtetéshez. The Review of Economics and Statistics 90: 417-427.