Podívejme se, jak to funguje

V Bayesovských modelech VAR jsme ukázali základní Bayesovskou analýzu IRF s použitím makrodat USA, což jsou čtvrtletní údaje od prvního čtvrtletí roku 1954 do čtvrtého čtvrtletí roku 2010. Zde si ukážeme další příklady bayesovské IRF a FEVD analýzy.

Chceme studovat vztahy mezi inflací, mezerou výstupu a sazbou federálních fondů. Zejména nás zajímá vliv sazby federálních fondů na ostatní výsledky v modelu.

Zde jsou data.

. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)

. tsset

Time variable: date, 1954q3 to 2010q4
        Delta: 1 quarter

. tsline inflation ogap fedfunds

Použili jsme bayesovský VAR model se třemi zpožděními. Výstup z něj zde potlačíme, ale více informací o příkazu si můžete přečíst v části Bayesian VAR model.

. quietly bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds, lags(1/3)

Nový příkaz bayesirf poskytuje několik dílčích příkazů pro bayesovskou analýzu IRF a FEVD. Tři hlavní jsou bayesirf create, bayesirf graph, a bayesirf table. bayesirf create vypočítá IRF a další funkce a uloží je do datové sady IRF, bayesirf graph je vykreslí a bayesirf table je zobrazí v tabulce. Další dílčí příkazy umožňují kombinovat grafy a tabulky více funkcí a spravovat výsledky IRF; viz [BAYES] bayesirf.

V klasické analýze je IRF (a další funkce) jedinou funkcí pro dané proměnné odezvy a impulsu. V bayesovské analýze získáme celý MCMC vzorek IRF simulovaný z posteriorního rozdělení. Tento vzorek je shrnut tak, aby vznikla jediná statistika, například posteriorní střední IRF nebo posteriorní medián IRF.

Začneme vytvořením IRF a dalších funkcí. Naše výsledky IRF pojmenujeme jako birf a uložíme je do datové sady Stata birfex.irf.

. bayesirf create birf, set(birfex)
(file birfex.irf created)
(file birfex.irf now active)
(file birfex.irf updated)

Dále vykreslíme IRF s fedfunds jako impulsní proměnnou.

. bayesirf graph irf, impulse(fedfunds)

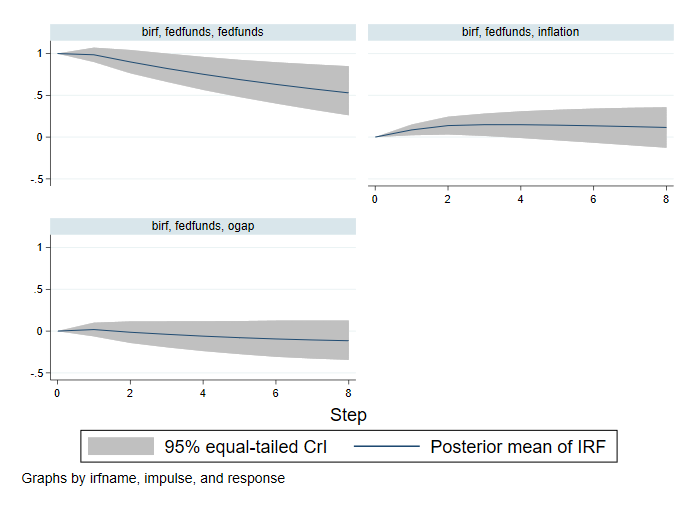
Šok na sazbu federálních fondů má sám o sobě pozitivní vliv, který se v čase snižuje, ale po osmi čtvrtletích je stále pozitivní. Šok ze sazby federálních fondů má malý vliv na mezeru výstupu a malý pozitivní vliv na inflaci, který po dvou čtvrtletích mizí.

Výsledky si můžeme prohlédnout v tabulce.

. bayesirf table irf, response(ogap) impulse(fedfunds)

Results from birf



         
 
      (1)         (1)         (1)  
    Step 
 
      irf       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .018505    -.062511      .10086
       2 
 
 -.013814    -.141146     .116743
       3 
 
 -.038081    -.193427     .117507
       4 
 
 -.060205    -.238349     .118354
       5 
 
 -.078581    -.275435     .120713
       6 
 
 -.093737    -.307345     .126362
       7 
 
 -.105821    -.328061     .126226
       8 
 
 -.115108    -.344162     .127231

Posterior means reported.
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = ogap.

Účinky šoku můžeme sledovat v delším časovém horizontu zadáním více časových období v parametru step() příkazu bayesirf create. Nahradíme aktuální výsledky a navíc uložíme vzorek IRF MCMC do souboru birfsim.dta.. (Výsledky IRF MCMC potřebujeme, pokud chceme vypočítat jiné věrohodné intervaly než výchozí 95% intervaly s rovným chvostem pomocí dílčích příkazů bayesirf, což si ukážeme později).

. bayesirf create birf, set(birfex) step(25) mcmcsaving(birfsim) replace
(file birfex.irf now active)
file birfsim.dta saved.
(file birfex.irf updated)

. bayesirf graph irf, impulse(fedfunds)

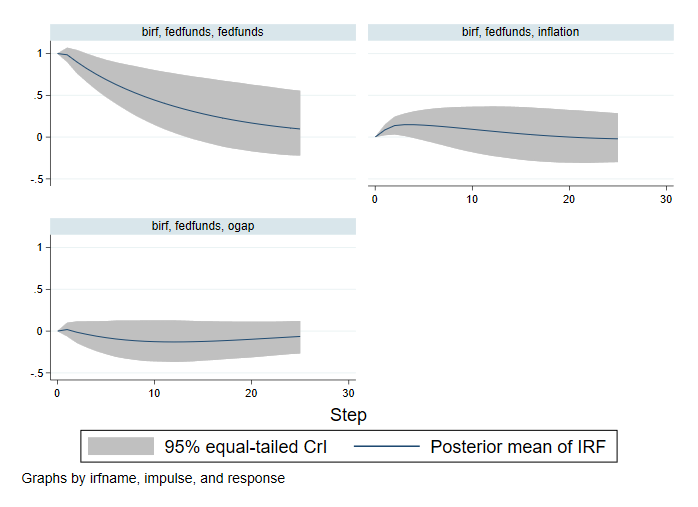
Přidání dalších časových období nám umožňuje dále zkoumat dynamiku sazby federálních fondů. Šok na sazbu federálních fondů má sám o sobě pozitivní vliv po dobu prvních 14 čtvrtletí. V předchozím příkladu s kratším horizontem jsme tento efekt nemohli pozorovat. Naše závěry o vlivu sazby federálních fondů na ostatní proměnné zůstávají stejné.

Můžeme se podívat na další funkce a vykreslit je vedle sebe pomocí bayesirf cgraph. Vykreslíme ortogonální IRF a FEVD.

. bayesirf cgraph (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd)

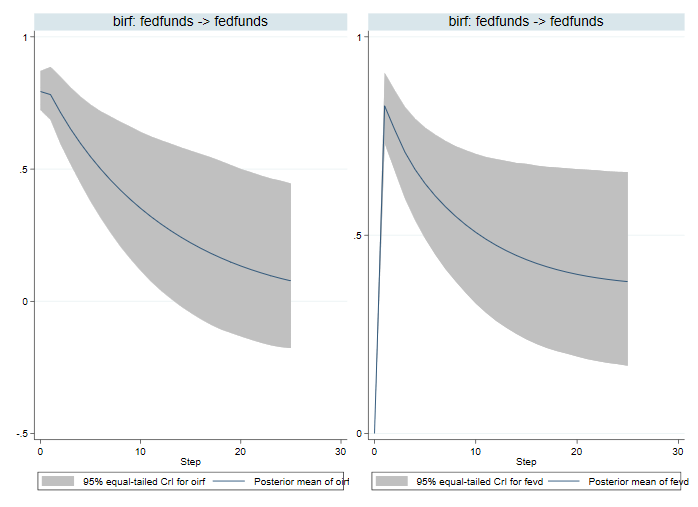
Ortogonální IRF (OIRF) popisují impulzní odezvu na šok o jedné standardní odchylce. FEVD měří podíl rozptylu chyby, který je vysvětlen šokem sazby federálních fondů. OIRF podporují naše předchozí závěry založené na IRF. FEVD ukazuje, že šok fedfunds převažuje v prvním kroku, ale pak se v průběhu času snižuje.

Více výsledků můžeme také zobrazit v tabulce pomocí bayesirf ctable. Pro stručnost uvádíme pouze první tři kroky.

. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3)



         
 
      (1)         (1)         (1)  
    Step 
 
     oirf       Lower       Upper  

       0 
 
  .793208      .72369     .870942
       1 
 
  .781637     .686623     .886267
       2 
 
  .713651     .594886     .848175
       3 
 
  .652003     .518588     .808557





         
 
      (1)         (1)         (1)  
    Step 
 
     fevd       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .825878     .731612     .909342
       2 
 
  .765772     .661851      .86463
       3 
 
  .709687     .593096     .823202

Posterior means reported.
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = fedfunds.

Místo výchozích posteriorních průměrů a rovnoměrných věrohodných intervalů můžeme uvádět posteriorní mediány a HPD věrohodné intervaly. (Můžeme to udělat, protože jsme již dříve uložili výsledky IRF MCMC pomocí bayesirf create.)

. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3) median hpd



         
 
      (1)         (1)         (1)  
    Step 
 
     oirf       Lower       Upper  

       0 
 
   .79167     .720032      .86681
       1 
 
  .780219     .686243     .884995
       2 
 
    .7111     .590842     .842952
       3 
 
  .648349     .512718     .799466





         
 
      (1)         (1)         (1)  
    Step 
 
     fevd       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .827376     .737115     .913222
       2 
 
  .766713     .664094     .865899
       3 
 
  .710221     .593963     .823788

Posterior medians reported.
95% HPD credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = fedfunds.

Pomocí volby clevel() můžete také změnit výchozí 95% hladinu věrohodnosti.

Po analýze odstraníme soubory vytvořené pomocí bayes: var a bayesirf create, pokud je již nepotřebujeme.

. erase bvarsim.dta
. erase birfsim.dta
. erase birfex.irf