Lássuk hogyan működiket

Bayesi VAR-modellekben az alapos Bayesi IRF-elemzést mutattuk be az Egyesült Államok makrodataival, amelyek 1954 első negyedévétől 2010 negyedik negyedévéig tartó negyedéves adatok. Itt további példákat mutatunk be a bayesi IRF és FEVD elemzésre.
Meg akarjuk vizsgálni az infláció, a kibocsátási rés és a szövetségi alapok arányának összefüggéseit. Különösen érdekel minket a szövetségi alapok arányának hatása a modell többi eredményére.
Itt van az adat.

. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)

. tsset

Time variable: date, 1954q3 to 2010q4
        Delta: 1 quarter

. tsline inflation ogap fedfunds

Három lemaradással illesztünk egy Bayes-i VAR modellt. Itt elnyomjuk a kimenetet, de a parancsról Bayesian VAR modellben olvashat bővebben.

. quietly bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds, lags(1/3)

Az új bayesirf parancs számos alparancsot biztosít a bayesi IRF és FEVD elemzéshez. Három fő a bayesirf létrehozása, a bayesirf create, bayesirf graph, és bayesirf table. bayesirf create az IRF-eket és más függvényeket, és elmenti azokat egy IRF-adatkészletbe, a bayesirf graph ábrázolja őket, és a bayesirf table egy táblázatban jeleníti meg őket. Más alparancsok lehetővé teszik több függvény grafikonjainak és tábláinak kombinálását és az IRF eredmények kezelését; lásd [BAYES] bayesirf.
A klasszikus elemzésben az IRF (és más funkciók) egyetlen függvény az adott válasz- és impulzusváltozókhoz. A Bayes-analízis során egy teljes MCMC mintát kapunk a hátsó eloszlásból szimulált IRF-ekből. Ezt a mintát összefoglalva egyetlen statisztikát állítunk elő, mint például a posterior átlag IRF vagy a posterior medián IRF.
Az IRF-ek és más funkciók létrehozásával kezdjük. Az IRF eredményeinket birf nevezzük, és a birfex.irf Stata adatkészletbe mentjük.

. bayesirf create birf, set(birfex)
(file birfex.irf created)
(file birfex.irf now active)
(file birfex.irf updated)

Ezután az IRF-et ábrázoljuk fedfundokkal, mint impulzus változóval.

. bayesirf graph irf, impulse(fedfunds)

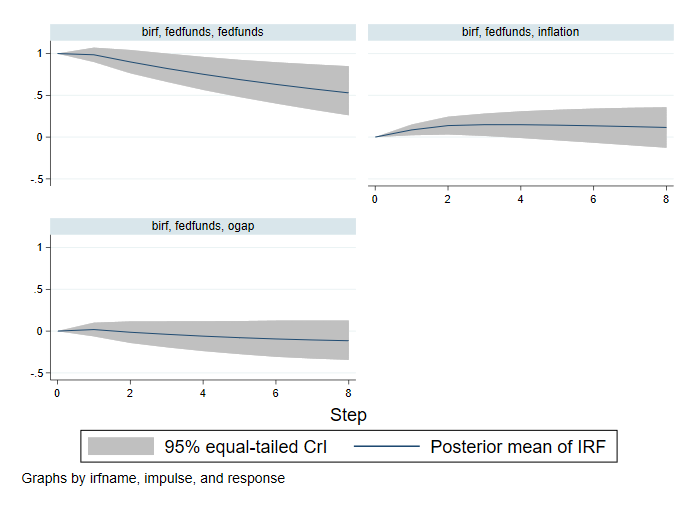
A szövetségi alapok arányának sokkja pozitív hatással van önmagára, amely idővel csökken, de nyolc negyedév után is pozitív. A szövetségi alapok kamat-sokkja alig befolyásolja a kibocsátási rést, és kicsi pozitív hatással van az inflációra, amely két negyedév után eltűnik.
Az eredményeket egy táblázatban láthatjuk.

. bayesirf table irf, response(ogap) impulse(fedfunds)

Results from birf



         
 
      (1)         (1)         (1)  
    Step 
 
      irf       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .018505    -.062511      .10086
       2 
 
 -.013814    -.141146     .116743
       3 
 
 -.038081    -.193427     .117507
       4 
 
 -.060205    -.238349     .118354
       5 
 
 -.078581    -.275435     .120713
       6 
 
 -.093737    -.307345     .126362
       7 
 
 -.105821    -.328061     .126226
       8 
 
 -.115108    -.344162     .127231

Posterior means reported.
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = ogap.

A sokk hatásait hosszabb távon láthatjuk, ha több időtartamot határoz meg a bayesirf create step() opciójában. Cseréljük a jelenlegi eredményeket, és az IRF MCMC mintát a birfsim.dta fájlba mentjük. (Szükségünk van az IRF MCMC eredményekre, ha az alapértelmezett 95% -os egyenfarú intervallumoktól eltérő hiteles intervallumokat akarunk kiszámítani a bayesirf alparancsokkal, amelyeket később bemutatunk.) x

. bayesirf create birf, set(birfex) step(25) mcmcsaving(birfsim) replace
(file birfex.irf now active)
file birfsim.dta saved.
(file birfex.irf updated)

. bayesirf graph irf, impulse(fedfunds)

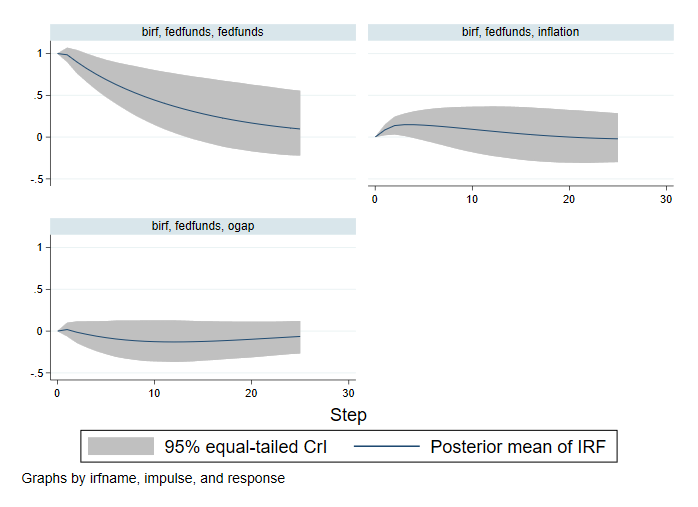
További időszakok hozzáadása lehetővé teszi számunkra, hogy tovább vizsgáljuk a szövetségi alapok kamatlábát. A szövetségi alapok arányának megrázkódtatása pozitív hatással van önmagára az első 14 negyedévben. Ezt a hatást az előző példában nem tudtuk megfigyelni rövidebb látóhatárral. A szövetségi alapok más változókra gyakorolt hatására vonatkozó következtetéseink ugyanazok maradnak.
A bayesirf cgraph. segítségével megnézhetünk más funkciókat, és egymás mellé rajzolhatjuk őket. Ábrázoljuk az ortogonális IRF-et és FEVD-t.

. bayesirf cgraph (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd)

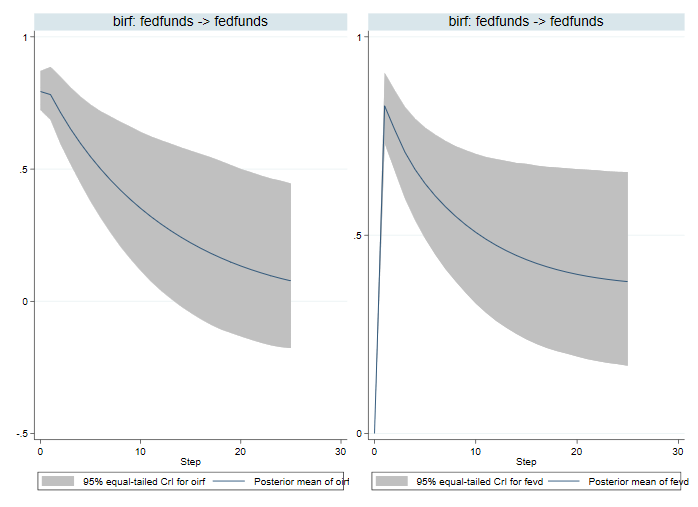
Az ortogonális IRF-ek (OIRF-ek) leírják az impulzus választ egy standard deviációs sokkra. A FEVD méri a hiba szórásának azon részét, amelyet a szövetségi alapok arányának sokkja magyaráz. Az OIRF-ek alátámasztják az IRF-ekre alapozott korábbi következtetéseinket. A FEVD azt mutatja, hogy a fedfunds sokkja első lépésben elterjedt, de az idő múlásával csökken.
Több eredményt is megjeleníthetünk egy táblázatban a bayesirf ctable használatával. A rövidség kedvéért csak az első három lépést mutatjuk be.

. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3)



         
 
      (1)         (1)         (1)  
    Step 
 
     oirf       Lower       Upper  

       0 
 
  .793208      .72369     .870942
       1 
 
  .781637     .686623     .886267
       2 
 
  .713651     .594886     .848175
       3 
 
  .652003     .518588     .808557





         
 
      (1)         (1)         (1)  
    Step 
 
     fevd       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .825878     .731612     .909342
       2 
 
  .765772     .661851      .86463
       3 
 
  .709687     .593096     .823202

Posterior means reported.
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = fedfunds.

Az alapértelmezett hátsó középértékek és az egyenlő farkú hiteles intervallumok helyett a hátsó mediánokat és a HPD hiteles intervallumokat jelenthetjük. (Megtehetjük, mert az IRF MCMC eredményeket már korábban elmentettük a bayesirf create -be.)

. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3) median hpd



         
 
      (1)         (1)         (1)  
    Step 
 
     oirf       Lower       Upper  

       0 
 
   .79167     .720032      .86681
       1 
 
  .780219     .686243     .884995
       2 
 
    .7111     .590842     .842952
       3 
 
  .648349     .512718     .799466





         
 
      (1)         (1)         (1)  
    Step 
 
     fevd       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .827376     .737115     .913222
       2 
 
  .766713     .664094     .865899
       3 
 
  .710221     .593963     .823788

Posterior medians reported.
95% HPD credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = fedfunds.

A clevel() opcióval módosíthatja az alapértelmezett 95% -os hiteles szintet is.
Elemzés után eltávolítjuk a bayes: var és bayesirf create fájlokat, ha már nincs rájuk szükség.

. erase bvarsim.dta
. erase birfsim.dta
. erase birfex.irf