Interval-censored Cox model

New In

Interval-censored Cox model

Often, time-to-event or failure-time data are collected at particular observation times. But sometimes, the event of interest is not observed exactly but is only known to occur within some time interval. For example, a physician will detect the recurrence of cancer only when the patient comes to the clinic for a follow-up appointment, and an epidemiologist who studies the COVID-19 incubation period will only know the infection occured before the patient shows symptoms or tests positive for COVID-19. In statistics, data like these are called interval-censored event-time data. Interval-censored event-time data arise in many areas, including medical, epidemiological, financial, and sociological studies. Ignoring interval-censoring may lead to biased estimates.

Just like with right-censored data, the Cox proportional hazards model is appealing for interval-censored data because it does not require parameterization of the baseline hazard function, and for low event rates, the exponentiated regression parameters approximate the log relative-risks.

In Stata 17, the new estimation command stintcox fits the semiparametric Cox proportional hazards models to interval-censored event-time data. The command can analyze data that include all types of censoring, including current-status data, in which the event of interest is known to occur only before or after an observed time. It also supports stratification.

Highlights

Genuine semiparametric modeling
Current-status and general interval-censored data
Stratified estimation
Two estimators for baseline hazard
Two estimators for standard errors
Graphs of survivor, cumulative hazard, and hazard functions
Residual diagnostics
Graphical checks of proportional-hazards assumption

Let’s see it work

Estimation
Graphing survivor functions
Stratification
Checking proportional-hazards assumption
Additional resources

Estimation

We use data from Zeng, Mao, and Lin (2016), who study time to HIV infection in a cohort study of injecting drug users in Thailand. The dataset contains 1,124 subjects. Those subjects initially tested negative for the HIV virus. They were then followed and assessed for HIV-1 seropositivity through blood tests approximately every four months. Because the subjects were tested periodically, the exact time of HIV infection was not observed, but it was known to fall in intervals between blood tests with the lower and upper endpoints recorded in variables ltime and time.

We want to identify the factors that influence time to HIV infection. The factors we are interested in are age at recruitment (age), sex (male), history of needle sharing (needle), history of drug injection (inject), and whether a subject has been in jail at the time of recruitment (jail).

. use https://www.stata-press.com/data/r17/bts
(Bangkok Tenofovir Study (BTS))

. describe

Contains data from https://www.stata-press.com/data/r17/bts.dta
 Observations:         1,124                  Bangkok Tenofovir Study (BTS)
    Variables:             8                  15 Dec 2020 13:34
                                              (_dta has notes)


Variable      Storage   Display    Value

    name         type    format    label      Variable label

age             byte    %8.0g                 Age (in years)
male            byte    %8.0g      yesno      Male
needle          byte    %8.0g      yesno      Shared needles
jail            byte    %8.0g      yesno      Imprisoned
inject          byte    %8.0g      yesno      Injected drugs before recruitment
ltime           double  %10.0g                Last time seronegative for HIV-1
rtime           double  %10.0g                First time seropositive for HIV-1
age_mean        double  %10.0g                Centered age (in years)

Sorted by:

We fit a Cox proportional hazards model in which time to HIV infection depends on the above factors of interest. To make the interpretation of the baseline hazard function more reasonable, we will use the centered age variable, age_mean.

. stintcox age_mean i.male i.needle i.inject i.jail, interval(ltime rtime)
note: using adaptive step size to compute derivatives.

Performing EM optimization (showing every 100 iterations):
Iteration 0:    log likelihood = -1086.2564
Iteration 100:  log likelihood = -597.65634
Iteration 200:  log likelihood = -597.57555
Iteration 295:  log likelihood = -597.56443

Computing standard errors: ............................ done

Interval-censored Cox regression                    Number of obs     =  1,124
Baseline hazard: Reduced intervals                         Uncensored =      0
                                                        Left-censored =     41
                                                       Right-censored =    991
                                                       Interval-cens. =     92

                                                    Wald chi2(5)      =  17.10
Log likelihood = -597.56443                         Prob > chi2       = 0.0043


                               OPG
               Haz. ratio   std. err.      z    P>|z|     [95% conf. interval]

    age_mean     .9684341   .0126552    -2.45   0.014     .9439452    .9935582
 
        male  
        Yes      .6846949   .1855907    -1.40   0.162     .4025073    1.164717
 
      needle  
        Yes      1.275912   .2279038     1.36   0.173     .8990401    1.810768
 
      inject  
        Yes      1.250154   .2414221     1.16   0.248     .8562184    1.825334
 
        jail  
        Yes      1.567244   .3473972     2.03   0.043     1.014982    2.419998

Note: Standard-error estimates may be more variable for small datasets and
      datasets with low proportions of interval-censored observations.

We find that age at recruitment is associated with lower risk of HIV infection and being in jail at enrollment is associated with higher risk of HIV infection. Other factors are not statistically significant.

Graphing survivor functions

We can graph the baseline survival curve by using stcurve with all covariates set to 0.

. stcurve, survival at((zero) _all)

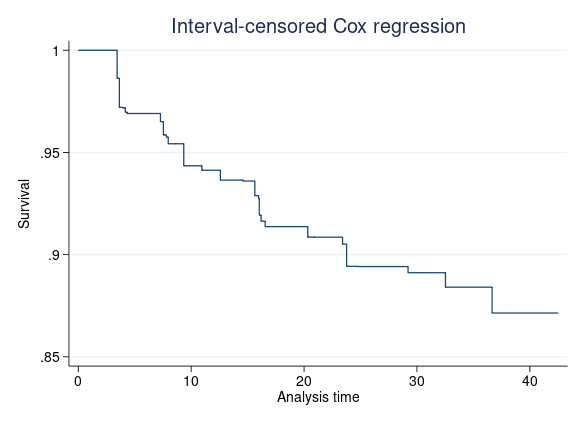
We can also graph the survivor functions with covariates set to any value. Suppose we want to compare the survivor functions of an average subject in the female and male groups. We type

. stcurve, survival at(male=(0 1))

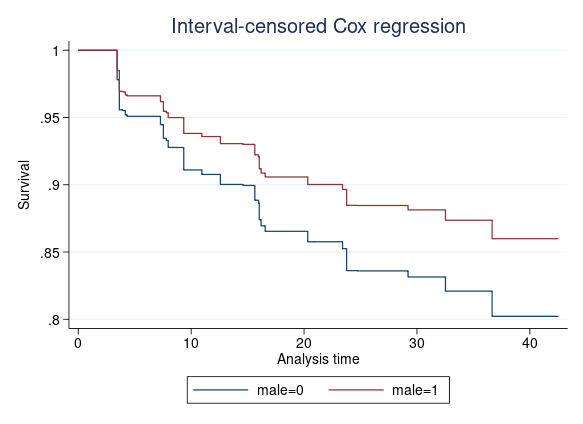
Stratification

If we assume that the baseline hazard function for female is different from that for male, we can fit a stratified Cox proportional hazards model by using the strata() option:

. stintcox age_mean i.needle i.inject i.jail, interval(ltime rtime) strata(male)
note: using adaptive step size to compute derivatives.

Performing EM optimization (showing every 100 iterations):
Iteration 0:    log likelihood = -1087.0536
Iteration 100:  log likelihood = -585.59848
Iteration 200:  log likelihood = -585.53143
Iteration 282:  log likelihood =  -585.5222

Computing standard errors: ........................... done

Stratified interval-censored Cox regression
Baseline hazard: Reduced intervals

Strata variable: male                               Number of obs     =  1,124
                                                           Uncensored =      0
                                                        Left-censored =     41
                                                       Right-censored =    991
                                                       Interval-cens. =     92

                                                    Wald chi2(4)      =  14.84
Log likelihood = -585.5222                          Prob > chi2       = 0.0051


                               OPG
               Haz. ratio   std. err.      z    P>|z|     [95% conf. interval]

    age_mean     .9682508   .0126326    -2.47   0.013     .9438052    .9933295
 
        male  
        Yes      1.276222   .2270302     1.37   0.170     .9005422    1.808625
 
      needle  
        Yes      1.245357   .2393768     1.14   0.254     .8544367    1.815131
 
      inject  
        Yes      1.245357   .2393768     1.14   0.254     .8544367    1.815131
 
        jail  
        Yes       1.57314   .3490687     2.04   0.041     1.018337    2.430205

Note: Standard-error estimates may be more variable for small datasets and
      datasets with low proportions of interval-censored observations.

Our conclusion here is similar to the case without stratification.

Checking proportional-hazards assumption

It is important to evaluate the validity of the underlying assumption for the Cox proportional hazards model, which is that the hazard ratio is constant over time. Stata 17 provides two new graphical commands to assess the proportional-hazards assumption.

For a single categorical covariate in a Cox model, you can use stintphplot, which plots -ln{-ln(survival)} curves for each category versus ln(analysis time). If the plots are parallel, the proportional-hazards assumption has not been violated. Alternatively, you can use stintcoxnp to plot the nonparametric maximum-likelihood estimation survival curve versus the Cox predicted survival curve for each category. When the two curves are close together, the proportional-hazards assumption is valid.

When a Cox model contains multiple covariates, as mentioned in the above example, only stintphplot is appropriate for testing the proportional-hazards assumption. In that case, we need to use the adjustfor() option.

For example, to check the proportional-hazards assumption for inject, we include all covariates except inject in the adjustfor() option:

. stintphplot, interval(ltime rtime) by(inject) adjustfor(age_mean i.male i.needle i.jail)

A separate Cox model, which contains all covariates from the adjustfor() option, is fit for each level of inject. And the two plots are almost parallel, which indicates that the proportional-hazards assumption has not been violated for the categorical variable inject.

Reference

Zeng, D., L. Mao, and D. Lin. 2016. Maximum likelihood estimation for semiparametric transformation models with interval-censored data. Biometrika 103: 253–271.

View all the new features

Order Stata 17

Upgrade