Nouveau dans 
Modèle de Cox à intervalles censurés
Souvent, les données de temps à événement ou de temps de défaillance sont collectées à des moments d’observation particuliers. Mais parfois, l’événement d’intérêt n’est pas observé exactement mais on sait seulement qu’il se produit dans un certain intervalle de temps. Par exemple, un médecin ne détectera la récidive d’un cancer que lorsque le patient se présentera à la clinique pour un rendez-vous de suivi, et un épidémiologiste qui étudie la période d’incubation du COVID-19 ne saura que l’infection a eu lieu avant que le patient ne présente des symptômes ou ne soit testé positif au COVID-19. En statistiques, les données de ce type sont appelées données événementielles à censure d’intervalle. Ces données sont utilisées dans de nombreux domaines, notamment dans les études médicales, épidémiologiques, financières et sociologiques. Ignorer la censure par intervalle peut conduire à des estimations biaisées.
Tout comme pour les données censurées à droite, le modèle des risques proportionnels de Cox est intéressant pour les données censurées par intervalle car il ne nécessite pas de paramétrage de la fonction de risque de base et, pour les faibles taux d’événements, les paramètres de régression exponentiels se rapprochent des risques relatifs logarithmiques.
In Stata 17, the new estimation command stintcox fits the semiparametric Cox proportional hazards models to interval-censored event-time data. The command can analyze data that include all types of censoring, including current-status data, in which the event of interest is known to occur only before or after an observed time. It also supports stratification.
Points forts
- Modélisation semi-paramétrique authentique
- État actuel et données générales censurées par intervalle
- Estimation stratifiée
- Deux estimateurs pour le risque de base
- Deux estimateurs pour les erreurs standard
- Graphiques des fonctions de survie, de risque cumulatif et de risque
- Diagnostics résiduels
- Vérifications graphiques de l’hypothèse d’aléas proportionnels
Voyons comment cela fonctionne
- Estimation
- Représentation graphique des fonctions de survie
- Stratification
- Vérification de l’hypothèse d’aléas proportionnels
- Ressources supplémentaires
Estimation
Nous utilisons les données de Zeng, Mao et Lin (2016), qui étudient le délai avant l’infection par le VIH dans une étude de cohorte de consommateurs de drogues injectables en Thaïlande. L’ensemble de données contient 1 124 sujets. Ces sujets ont initialement été testés négatifs pour le virus du VIH. Ils ont ensuite été suivis et évalués pour la séropositivité au VIH-1 par des tests sanguins environ tous les quatre mois. Comme les sujets ont été testés périodiquement, le moment exact de l’infection par le VIH n’a pas été observé, mais on sait qu’il tombe dans les intervalles entre les tests sanguins, les points finaux inférieurs et supérieurs étant enregistrés dans les variables ltime et time.
Nous voulons identifier les facteurs qui influencent le délai d’infection par le VIH. Les facteurs qui nous intéressent sont l’âge au moment du recrutement (âge), le sexe (homme), les antécédents de partage de seringue (aiguille), les antécédents d’injection de drogue (injection), et si un sujet a été en prison au moment du recrutement (prison).
. use https://www.stata-press.com/data/r17/bts
(Bangkok Tenofovir Study (BTS))
. describe
Contains data from https://www.stata-press.com/data/r17/bts.dta
Observations: 1,124 Bangkok Tenofovir Study (BTS)
Variables: 8 15 Dec 2020 13:34
(_dta has notes)
| Variable Storage Display Value | ||||||
| name type format label Variable label | ||||||
| age byte %8.0g Age (in years) | ||||||
| male byte %8.0g yesno Male | ||||||
| needle byte %8.0g yesno Shared needles | ||||||
| jail byte %8.0g yesno Imprisoned | ||||||
| inject byte %8.0g yesno Injected drugs before recruitment | ||||||
| ltime double %10.0g Last time seronegative for HIV-1 | ||||||
| rtime double %10.0g First time seropositive for HIV-1 | ||||||
| age_mean double %10.0g Centered age (in years) | ||||||
Nous avons ajusté un modèle de risques proportionnels de Cox dans lequel le délai avant l’infection par le VIH dépend des facteurs d’intérêt ci-dessus. Pour rendre l’interprétation de la fonction de risque de base plus raisonnable, nous utiliserons la variable d’âge centrée, age_mean.
. stintcox age_mean i.male i.needle i.inject i.jail, interval(ltime rtime)
note: using adaptive step size to compute derivatives.
Performing EM optimization (showing every 100 iterations):
Iteration 0: log likelihood = -1086.2564
Iteration 100: log likelihood = -597.65634
Iteration 200: log likelihood = -597.57555
Iteration 295: log likelihood = -597.56443
Computing standard errors: ............................ done
Interval-censored Cox regression Number of obs = 1,124
Baseline hazard: Reduced intervals Uncensored = 0
Left-censored = 41
Right-censored = 991
Interval-cens. = 92
Wald chi2(5) = 17.10
Log likelihood = -597.56443 Prob > chi2 = 0.0043
| OPG | ||||||
| Haz. ratio std. err. z P>|z| [95% conf. interval] | ||||||
| age_mean | .9684341 .0126552 -2.45 0.014 .9439452 .9935582 | |||||
| male | ||||||
| Yes | .6846949 .1855907 -1.40 0.162 .4025073 1.164717 | |||||
| needle | ||||||
| Yes | 1.275912 .2279038 1.36 0.173 .8990401 1.810768 | |||||
| inject | ||||||
| Yes | 1.250154 .2414221 1.16 0.248 .8562184 1.825334 | |||||
| jail | ||||||
| Yes | 1.567244 .3473972 2.03 0.043 1.014982 2.419998 | |||||
Nous constatons que l’âge au moment du recrutement est associé à un risque plus faible d’infection par le VIH et que le fait d’être en prison au moment du recrutement est associé à un risque plus élevé d’infection par le VIH. Les autres facteurs ne sont pas statistiquement significatifs..
Représentation graphique des fonctions de survie
Nous pouvons représenter graphiquement la courbe de survie de base en utilisant stcurve avec toutes les covariables fixées à 0..
. stcurve, survival at((zero) _all)
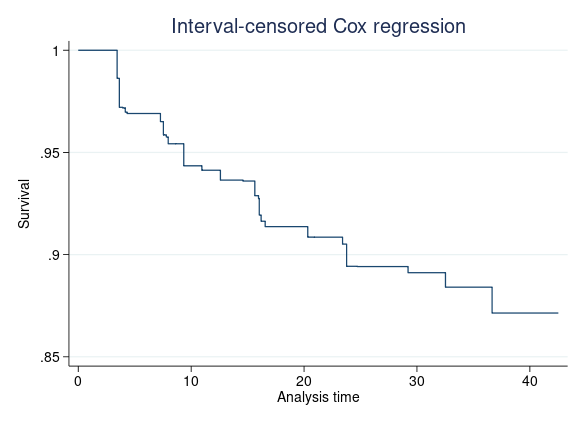
Nous pouvons également représenter graphiquement les fonctions de survie avec des covariables dont la valeur est quelconque. Supposons que nous voulions comparer les fonctions de survie d’un sujet moyen dans les groupes féminin et masculin. Nous tapons
. stcurve, survival at(male=(0 1))
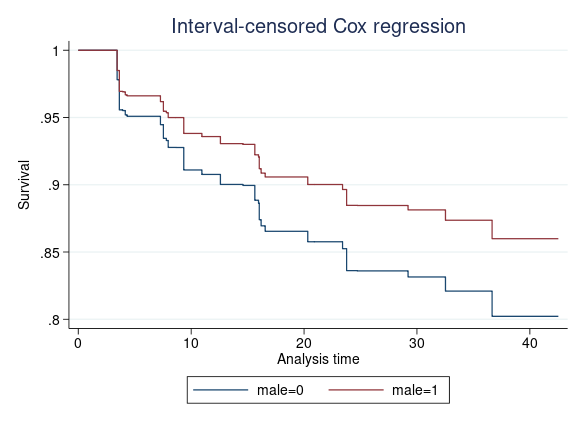
Stratification
Si nous supposons que la fonction de risque de base pour les femmes est différente de celle des hommes, nous pouvons ajuster un modèle de risques proportionnels de Cox stratifié en utilisant l’option strata() :
. stintcox age_mean i.needle i.inject i.jail, interval(ltime rtime) strata(male)
note: using adaptive step size to compute derivatives.
Performing EM optimization (showing every 100 iterations):
Iteration 0: log likelihood = -1087.0536
Iteration 100: log likelihood = -585.59848
Iteration 200: log likelihood = -585.53143
Iteration 282: log likelihood = -585.5222
Computing standard errors: ........................... done
Stratified interval-censored Cox regression
Baseline hazard: Reduced intervals
Strata variable: male Number of obs = 1,124
Uncensored = 0
Left-censored = 41
Right-censored = 991
Interval-cens. = 92
Wald chi2(4) = 14.84
Log likelihood = -585.5222 Prob > chi2 = 0.0051
| OPG | ||||||
| Haz. ratio std. err. z P>|z| [95% conf. interval] | ||||||
| age_mean | .9682508 .0126326 -2.47 0.013 .9438052 .9933295 | |||||
| male | ||||||
| Yes | 1.276222 .2270302 1.37 0.170 .9005422 1.808625 | |||||
| needle | ||||||
| Yes | 1.245357 .2393768 1.14 0.254 .8544367 1.815131 | |||||
| inject | ||||||
| Yes | 1.245357 .2393768 1.14 0.254 .8544367 1.815131 | |||||
| jail | ||||||
| Yes | 1.57314 .3490687 2.04 0.041 1.018337 2.430205 | |||||
Notre conclusion ici est similaire au cas sans stratification.
Vérification de l’hypothèse des risques proportionnels
Il est important d’évaluer la validité de l’hypothèse sous-jacente du modèle des risques proportionnels de Cox, qui est que le rapport des risques est constant dans le temps. Stata 17 fournit deux nouvelles commandes graphiques pour évaluer l’hypothèse des risques proportionnels.
Pour une covariable catégorielle unique dans un modèle de Cox, vous pouvez utiliser stintphplot, qui trace des courbes -ln{-ln(survie)} pour chaque catégorie en fonction de ln(temps d’analyse). Si les courbes sont parallèles, l’hypothèse des risques proportionnels n’a pas été violée. Vous pouvez également utiliser stintcoxnp pour tracer la courbe de survie de l’estimation non paramétrique du maximum de vraisemblance par rapport à la courbe de survie prédite par Cox pour chaque catégorie. Lorsque les deux courbes sont proches l’une de l’autre, l’hypothèse des risques proportionnels est valide.
Lorsqu’un modèle de Cox contient de multiples covariables, comme mentionné dans l’exemple ci-dessus, seul stintphplot est approprié pour tester l’hypothèse d’aléas proportionnels. Dans ce cas, nous devons utiliser l’option adjustfor().
Par exemple, pour vérifier l’hypothèse des hasards proportionnels pour inject, nous incluons toutes les covariables sauf inject dans l’option adjustfor() :
. stintphplot, interval(ltime rtime) by(inject) adjustfor(age_mean i.male i.needle i.jail)

A separate Cox model, which contains all covariates from the adjustfor() option, is fit for each level of inject. And the two plots are almost parallel, which indicates that the proportional-hazards assumption has not been violated for the categorical variable inject.
Reference
Zeng, D., L. Mao, and D. Lin. 2016. Maximum likelihood estimation for semiparametric transformation models with interval-censored data. Biometrika 103: 253–271.
