Neu in 
Intervall-zensiertes Cox-Modell
Oft werden Ereignis- oder Ausfallzeitdaten zu bestimmten Beobachtungszeitpunkten erfasst. Aber manchmal wird das Ereignis von Interesse nicht genau beobachtet, sondern es ist nur bekannt, dass es innerhalb eines bestimmten Zeitintervalls auftritt. Zum Beispiel wird ein Arzt das Wiederauftreten einer Krebserkrankung nur dann feststellen, wenn der Patient zu einem Folgetermin in die Klinik kommt, und ein Epidemiologe, der die COVID-19-Inkubationszeit untersucht, wird nur wissen, dass die Infektion aufgetreten ist, bevor der Patient Symptome zeigt oder positiv auf COVID-19 getestet wird. In der Statistik werden Daten wie diese als intervallzensierte Ereigniszeitdaten bezeichnet. Intervallzensierte Ereigniszeitdaten treten in vielen Bereichen auf, einschließlich medizinischer, epidemiologischer, finanzieller und soziologischer Studien. Das Ignorieren der Intervallzensierung kann zu verzerrten Schätzungen führen. Genau wie bei rechtszensierten Daten ist das Cox-Proportional-Hazards-Modell für intervallzensierte Daten attraktiv, weil es keine Parametrisierung der Basislinien-Hazard-Funktion erfordert und für niedrige Ereignisraten die exponentiellen Regressionsparameter die log-Relativ-Risiken approximieren.
In Stata 17 passt der neue Schätzungsbefehl stintcox die semiparametrischen Cox-Proportional-Hazards-Modelle an intervallzensierte Ereigniszeitdaten an. Der Befehl kann Daten analysieren, die alle Arten von Zensierung enthalten, einschließlich Current-Status-Daten, bei denen bekannt ist, dass das interessierende Ereignis nur vor oder nach einem beobachteten Zeitpunkt auftritt. Er unterstützt auch die Stratifizierung.
Höhepunkte
- Echte semiparametrische Modellierung
- Ist-Zustand und allgemeine intervallzensierte Daten
- Stratifizierte Schätzung
- Zwei Schätzer für die Grundliniengefährdung
- Zwei Schätzer für Standardfehler
- Graphen für Überlebenszeit-, kumulative Hazard- und Hazard-Funktionen
- Residuale Diagnose
- Grafische Überprüfung der Proportional-Hazard-Annahme
Zeigen Sie, wie es funktioniert
- Schätzung
- Überlebensfunktionen grafisch darstellen
- Stratifizierung
- Prüfen der Proportional-Hazards-Annahme
- Zusätzliche Ressourcen
Schätzung
Wir verwenden Daten von Zeng, Mao und Lin (2016), die die Zeit bis zur HIV-Infektion in einer Kohortenstudie von injizierenden Drogenkonsumenten in Thailand untersuchen. Der Datensatz enthält 1.124 Probanden. Diese Probanden wurden zunächst negativ auf das HIV-Virus getestet. Sie wurden dann verfolgt und etwa alle vier Monate durch Bluttests auf HIV-1-Seropositivität untersucht. Da die Probanden in regelmäßigen Abständen getestet wurden, wurde der genaue Zeitpunkt der HIV-Infektion nicht beobachtet, aber es war bekannt, dass er in die Intervalle zwischen den Bluttests fiel, wobei der untere und obere Endpunkt in den Variablen ltime und time aufgezeichnet wurde.
Wir wollen die Faktoren identifizieren, die die Zeit bis zur HIV-Infektion beeinflussen. Die Faktoren, an denen wir interessiert sind, sind das Alter bei der Rekrutierung (Alter), das Geschlecht (männlich), die Geschichte der gemeinsamen Nutzung von Nadeln (Nadel), die Geschichte der Drogeninjektion (injizieren) und ob eine Person zum Zeitpunkt der Rekrutierung im Gefängnis war (Gefängnis).
. use https://www.stata-press.com/data/r17/bts
(Bangkok Tenofovir Study (BTS))
. describe
Contains data from https://www.stata-press.com/data/r17/bts.dta
Observations: 1,124 Bangkok Tenofovir Study (BTS)
Variables: 8 15 Dec 2020 13:34
(_dta has notes)
| Variable Storage Display Value | ||||||
| name type format label Variable label | ||||||
| age byte %8.0g Age (in years) | ||||||
| male byte %8.0g yesno Male | ||||||
| needle byte %8.0g yesno Shared needles | ||||||
| jail byte %8.0g yesno Imprisoned | ||||||
| inject byte %8.0g yesno Injected drugs before recruitment | ||||||
| ltime double %10.0g Last time seronegative for HIV-1 | ||||||
| rtime double %10.0g First time seropositive for HIV-1 | ||||||
| age_mean double %10.0g Centered age (in years) | ||||||
Wir passen ein Cox-Proportional-Hazard-Modell an, in dem die Zeit bis zur HIV-Infektion von den oben genannten interessierenden Faktoren abhängt. Um die Interpretation der Baseline-Hazard-Funktion sinnvoller zu gestalten, werden wir die zentrierte Altersvariable, age_mean, verwenden.
. stintcox age_mean i.male i.needle i.inject i.jail, interval(ltime rtime)
note: using adaptive step size to compute derivatives.
Performing EM optimization (showing every 100 iterations):
Iteration 0: log likelihood = -1086.2564
Iteration 100: log likelihood = -597.65634
Iteration 200: log likelihood = -597.57555
Iteration 295: log likelihood = -597.56443
Computing standard errors: ............................ done
Interval-censored Cox regression Number of obs = 1,124
Baseline hazard: Reduced intervals Uncensored = 0
Left-censored = 41
Right-censored = 991
Interval-cens. = 92
Wald chi2(5) = 17.10
Log likelihood = -597.56443 Prob > chi2 = 0.0043
| OPG | ||||||
| Haz. ratio std. err. z P>|z| [95% conf. interval] | ||||||
| age_mean | .9684341 .0126552 -2.45 0.014 .9439452 .9935582 | |||||
| male | ||||||
| Yes | .6846949 .1855907 -1.40 0.162 .4025073 1.164717 | |||||
| needle | ||||||
| Yes | 1.275912 .2279038 1.36 0.173 .8990401 1.810768 | |||||
| inject | ||||||
| Yes | 1.250154 .2414221 1.16 0.248 .8562184 1.825334 | |||||
| jail | ||||||
| Yes | 1.567244 .3473972 2.03 0.043 1.014982 2.419998 | |||||
Wir stellen fest, dass das Alter bei der Rekrutierung mit einem geringeren Risiko für eine HIV-Infektion verbunden ist und dass ein Gefängnisaufenthalt bei der Rekrutierung mit einem höheren Risiko für eine HIV-Infektion verbunden ist. Andere Faktoren sind statistisch nicht signifikant.
Überlebensfunktionen grafisch darstellen
Wir können die Basislinien-Überlebenskurve grafisch darstellen, indem wir stcurve mit allen Kovariaten auf 0 setzen.
. stcurve, survival at((zero) _all)
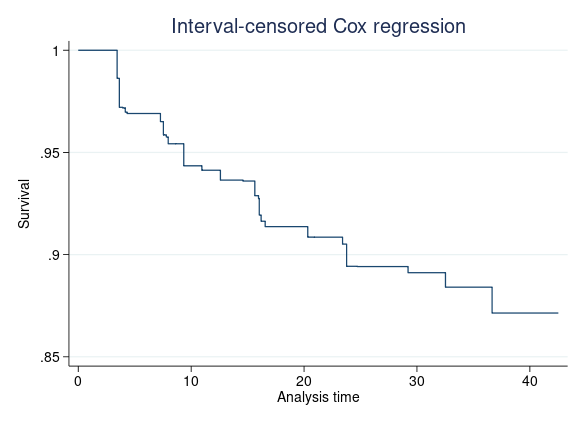
Wir können die Überlebensfunktionen auch grafisch darstellen, wenn die Kovariablen auf einen beliebigen Wert gesetzt sind. Angenommen, wir möchten die Überlebensfunktionen eines durchschnittlichen Probanden in der weiblichen und männlichen Gruppe vergleichen. Wir geben ein
. stcurve, survival at(male=(0 1))
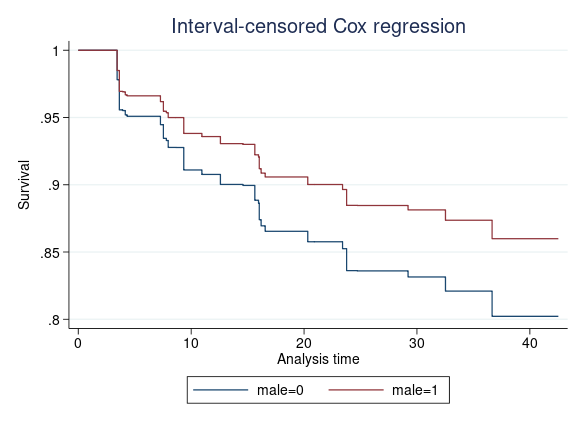
Stratifizierung
Wenn wir davon ausgehen, dass sich die Basis-Hazard-Funktion für Frauen von der für Männer unterscheidet, können wir ein stratifiziertes Cox-Proportional-Hazard-Modell anpassen, indem wir die Option strata() verwenden:
. stintcox age_mean i.needle i.inject i.jail, interval(ltime rtime) strata(male)
note: using adaptive step size to compute derivatives.
Performing EM optimization (showing every 100 iterations):
Iteration 0: log likelihood = -1087.0536
Iteration 100: log likelihood = -585.59848
Iteration 200: log likelihood = -585.53143
Iteration 282: log likelihood = -585.5222
Computing standard errors: ........................... done
Stratified interval-censored Cox regression
Baseline hazard: Reduced intervals
Strata variable: male Number of obs = 1,124
Uncensored = 0
Left-censored = 41
Right-censored = 991
Interval-cens. = 92
Wald chi2(4) = 14.84
Log likelihood = -585.5222 Prob > chi2 = 0.0051
| OPG | ||||||
| Haz. ratio std. err. z P>|z| [95% conf. interval] | ||||||
| age_mean | .9682508 .0126326 -2.47 0.013 .9438052 .9933295 | |||||
| male | ||||||
| Yes | 1.276222 .2270302 1.37 0.170 .9005422 1.808625 | |||||
| needle | ||||||
| Yes | 1.245357 .2393768 1.14 0.254 .8544367 1.815131 | |||||
| inject | ||||||
| Yes | 1.245357 .2393768 1.14 0.254 .8544367 1.815131 | |||||
| jail | ||||||
| Yes | 1.57314 .3490687 2.04 0.041 1.018337 2.430205 | |||||
Unsere Schlussfolgerung ist hier ähnlich wie im Fall ohne Stratifizierung.
Überprüfung der Proportional-Hazard-Annahme
Es ist wichtig, die Gültigkeit der zugrundeliegenden Annahme für das Cox Proportional-Hazards-Modell zu bewerten, die darin besteht, dass das Hazard Ratio über die Zeit konstant ist. Stata 17 bietet zwei neue grafische Befehle zur Beurteilung der Proportional-Hazards-Annahme.
Für eine einzelne kategoriale Kovariate in einem Cox-Modell können Sie stintphplot verwenden, das -ln{-ln(Überleben)}-Kurven für jede Kategorie gegen ln(Analysezeit) aufträgt. Wenn die Diagramme parallel sind, wurde die Proportionalitätsannahme nicht verletzt. Alternativ können Sie stintcoxnp verwenden, um die nichtparametrische Überlebenskurve der Maximum-Likelihood-Schätzung gegen die Cox-Vorhersagekurve für jede Kategorie darzustellen. Wenn die beiden Kurven nahe beieinander liegen, ist die Proportional-Hazard-Annahme gültig.
Wenn ein Cox-Modell mehrere Kovariaten enthält, wie im obigen Beispiel erwähnt, ist nur stintphplot für das Testen der Proportional-Hazard-Annahme geeignet. In diesem Fall müssen wir die Option adjustfor() verwenden.
Um zum Beispiel die Proportional-Hazard-Annahme für inject zu überprüfen, schließen wir alle Kovariaten außer inject in die adjustfor()-Option ein:
. stintphplot, interval(ltime rtime) by(inject) adjustfor(age_mean i.male i.needle i.jail)

Ein separates Cox-Modell, das alle Kovariaten aus der adjustfor()-Option enthält, wird für jede Stufe von inject angepasst. Und die beiden Diagramme sind fast parallel, was darauf hinweist, dass die Proportional-Hazard-Annahme für die kategoriale Variable inject nicht verletzt wurde.
Referenz
Zeng, D., L. Mao, und D. Lin. 2016. Maximum-Likelihood-Schätzung für semiparametrische Transformationsmodelle mit intervallzensierten Daten. Biometrika 103: 253-271.
