• Becslés
• A túlélő funkciók ábrázolása
• Rétegzés
• Az arányos-veszély feltételezés ellenőrzése
• További források

Becslés

Zeng, Mao és Lin (2016) adatait használjuk, akik a thaiföldi injekciós drogfogyasztók kohorszos tanulmányában tanulmányozzák a HIV-fertőzésig eltelt időt. Az adatkészlet 1124 alanyt tartalmaz. Az alanyok elözetesen negtív tesztet adtak HIV vírusra. Ezután körülbelül négy havonta vérvizsgálatok útján követték őket és értékelték a HIV-1 szeropozitivitását. Mivel az alanyokat periodikusan tesztelték, a HIV-fertőzés pontos idejét nem figyelték meg, de ismert volt, hogy a vérvizsgálatok közötti időre esett, az alsó és felső végponttal az ltime és az time változóban rögzítve. Az általunk érdekelt tényezők a felvételkora (életkor), neme (férfi), a tűmegosztás története (tű), a kábítószer beadás története (injekció), valamint az, hogy az alany a börtönben volt-e a felvétel idején (börtön).

. use https://www.stata-press.com/data/r17/bts
(Bangkok Tenofovir Study (BTS))

. describe

Contains data from https://www.stata-press.com/data/r17/bts.dta
 Observations:         1,124                  Bangkok Tenofovir Study (BTS)
    Variables:             8                  15 Dec 2020 13:34
                                              (_dta has notes)


Variable      Storage   Display    Value

    name         type    format    label      Variable label

age             byte    %8.0g                 Age (in years)
male            byte    %8.0g      yesno      Male
needle          byte    %8.0g      yesno      Shared needles
jail            byte    %8.0g      yesno      Imprisoned
inject          byte    %8.0g      yesno      Injected drugs before recruitment
ltime           double  %10.0g                Last time seronegative for HIV-1
rtime           double  %10.0g                First time seropositive for HIV-1
age_mean        double  %10.0g                Centered age (in years)

Sorted by:

Cox arányos kockázati modellt illesztünk be, amelyben a HIV-fertőzésig tartó idő függ a fenti érdeklődésre számot tartó tényezőktől. Az alapveszély-függvény értelmezésének ésszerűbbé tétele érdekében a középkorú életkor-változót, az age_mean-t fogjuk használni.

. stintcox age_mean i.male i.needle i.inject i.jail, interval(ltime rtime)
note: using adaptive step size to compute derivatives.

Performing EM optimization (showing every 100 iterations):
Iteration 0:    log likelihood = -1086.2564
Iteration 100:  log likelihood = -597.65634
Iteration 200:  log likelihood = -597.57555
Iteration 295:  log likelihood = -597.56443

Computing standard errors: ............................ done

Interval-censored Cox regression                    Number of obs     =  1,124
Baseline hazard: Reduced intervals                         Uncensored =      0
                                                        Left-censored =     41
                                                       Right-censored =    991
                                                       Interval-cens. =     92

                                                    Wald chi2(5)      =  17.10
Log likelihood = -597.56443                         Prob > chi2       = 0.0043


             
 
                 OPG
             
 
 Haz. ratio   std. err.      z    P>|z|     [95% conf. interval]

    age_mean 
 
   .9684341   .0126552    -2.45   0.014     .9439452    .9935582
 

        male 
 

        Yes  
 
   .6846949   .1855907    -1.40   0.162     .4025073    1.164717
 

      needle 
 

        Yes  
 
   1.275912   .2279038     1.36   0.173     .8990401    1.810768
 

      inject 
 

        Yes  
 
   1.250154   .2414221     1.16   0.248     .8562184    1.825334
 

        jail 
 

        Yes  
 
   1.567244   .3473972     2.03   0.043     1.014982    2.419998

Note: Standard-error estimates may be more variable for small datasets and
      datasets with low proportions of interval-censored observations.

Megállapítottuk, hogy a toborzáskorban a HIV-fertőzésnek alacsonyabb kockázata van, a beiratkozáskor pedig börtönben van a magasabb HIV-fertőzés. Más tényezők statisztikailag nem szignifikánsak.

A túlélő függvények ábrázolása

Az alapvonali túlélési görbét ábrázolhatjuk úgy, hogy stcurve-t használunk, az összes kovariátus értéke 0

. stcurve, survival at((zero) _all)

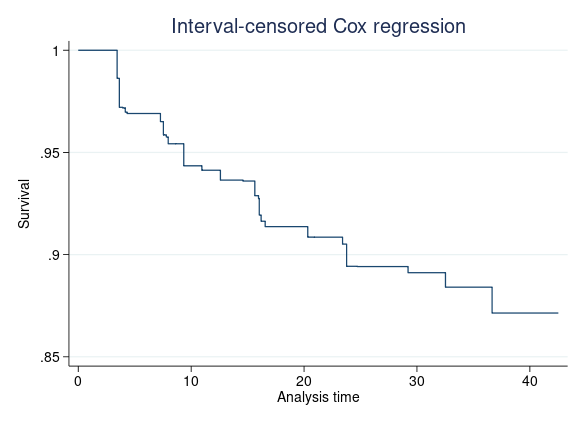
A túlélő függvényeket ábrázolhatjuk bármilyen értékre beállított kovariánsokkal is. Tegyük fel, hogy egy átlagos alany túlélő funkcióit szeretnénk összehasonlítani a női és a férfi csoportban. Begépeljük

. stcurve, survival at(male=(0 1))

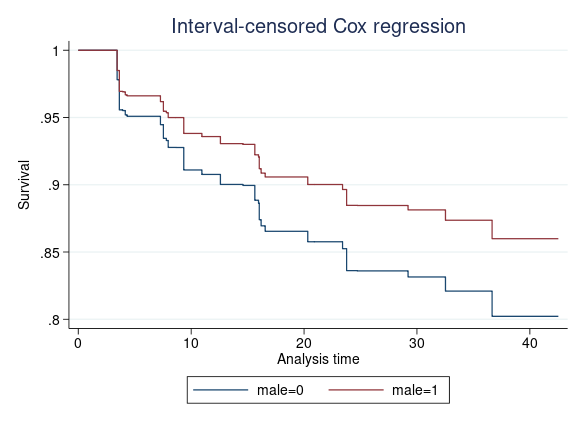
Rétegzés

Ha azt feltételezzük, hogy a female esetében a veszélyességi függvény eltér a male, a strata() opció használatával illeszthetünk egy rétegzett Cox arányos veszélyességi modellt:

. stintcox age_mean i.needle i.inject i.jail, interval(ltime rtime) strata(male)
note: using adaptive step size to compute derivatives.

Performing EM optimization (showing every 100 iterations):
Iteration 0:    log likelihood = -1087.0536
Iteration 100:  log likelihood = -585.59848
Iteration 200:  log likelihood = -585.53143
Iteration 282:  log likelihood =  -585.5222

Computing standard errors: ........................... done

Stratified interval-censored Cox regression
Baseline hazard: Reduced intervals

Strata variable: male                               Number of obs     =  1,124
                                                           Uncensored =      0
                                                        Left-censored =     41
                                                       Right-censored =    991
                                                       Interval-cens. =     92

                                                    Wald chi2(4)      =  14.84
Log likelihood = -585.5222                          Prob > chi2       = 0.0051


             
 
                 OPG
             
 
 Haz. ratio   std. err.      z    P>|z|     [95% conf. interval]

    age_mean 
 
   .9682508   .0126326    -2.47   0.013     .9438052    .9933295
 

        male 
 

        Yes  
 
   1.276222   .2270302     1.37   0.170     .9005422    1.808625
 

      needle 
 

        Yes  
 
   1.245357   .2393768     1.14   0.254     .8544367    1.815131
 

      inject 
 

        Yes  
 
   1.245357   .2393768     1.14   0.254     .8544367    1.815131
 

        jail 
 

        Yes  
 
    1.57314   .3490687     2.04   0.041     1.018337    2.430205

Note: Standard-error estimates may be more variable for small datasets and
      datasets with low proportions of interval-censored observations.

Következtetésünk itt hasonló a rétegződés nélküli esethez.

Az arányos-veszély feltételezés ellenőrzése

Fontos értékelni a Cox arányos veszélyességi modell alapjául szolgáló feltételezés érvényességét, miszerint a veszélyességi arány állandó az idő múlásával. A Stata 17.két új grafikus parancsot ad az arányos veszélyek feltételezésének értékelésére.
A Cox modell egyetlen kategóriás kovariánsához használhatja a stintphplot, -ot, amely az egyes kategóriákhoz ln {-ln (survival)} görbéket ábrázol az ln-vel szemben (analysis time).Ha a parcellák párhuzamosak, az arányos-veszély feltételezést nem sértették meg.
Alternatív megoldásként a stintcoxnp segítségével megrajzolhatja a nem-paraméteres maximális valószínűség becslés túlélési görbét a Cox által előre jelzett túlélési görbével szemben az egyes kategóriákhoz. Amikor a két görbe közel van egymáshoz, az arányos-veszély feltételezés érvényes. Ha a Cox modell több kovariátot tartalmaz, amint azt a fenti példa említi, akkor csak a stintphplot alkalmas az arányos veszélyek feltételezésének tesztelésére. Ebben az esetben az adjustfor() opciót kell használnunk.
Például az inject, kapcsolatos arányos kockázatok feltételezésének ellenőrzéséhez az összes injekciót kivéve az inject az adjustfor() opcióba foglaljuk:

. stintphplot, interval(ltime rtime) by(inject) adjustfor(age_mean i.male i.needle i.jail)

Az inject minden szintjére külön Cox modell illik, amely tartalmazza az összes kovariátumot a adjustfor() opciótól. És a két ábra szinte párhuzamos, ami azt jelzi, hogy az arányos-veszély feltételezést nem sértette meg az inject.

Referenciák

Zeng, D., L. Mao, and D. Lin. 2016. Maximum likelihood estimation for semiparametric transformation models with interval-censored data. Biometrika 103: 253–271.