New In 
Kvantilová regrese instrumentálních proměnných
Pokud chceme studovat vliv kovariát na různé kvantily výsledku, použijeme kvantilovou regresi. Ale co když máme podezření, že kovarianta je endogenní? Nový příkaz ivqregress modeluje kvantily výsledku a zároveň kontroluje problémy, které vyplývají z endogenity.
Nejdůležitější informace
-
Kvantilové odhady instrumentálních proměnných (IV)
-
Inverzní kvantilová regrese (IQR)
-
Vyhlazené odhadní rovnice
-
-
Odhad IQR
-
Intervaly spolehlivosti odolné vůči slabým nástrojům
-
Grafická diagnostika konvergence
-
-
Simultánní odhad přes kvantily
-
Vizualizace efektů nad kvantily
-
Specializované testy
-
IV nemá vliv na výsledek
-
Rovnost endogenních účinků napříč kvantily
-
Efekty větší než nula napříč kvantily
-
IV je exogenní místo endogenní
-
Přehled
Při použití lineární regrese modelujeme střední hodnotu výsledku. Někdy bychom však chtěli studovat i jiné vlastnosti rozdělení výsledku, než je průměr. Například tvůrce politiky může chtít zjistit, jak by účast v penzijním plánu 401(k) ovlivnila podmíněné kvantily čistého jmění na nižší, střední a vyšší úrovni.
ivqregress odhaduje parametry na kvantilech rozdělení výsledků a zohledňuje problémy s endogenitou, které vznikají z důvodů, jako je samovýběr, opomenutí příslušné proměnné nebo chyba měření. Například účast v programu 401(k) může být endogenní, protože lidé, kteří se ho účastní a neúčastní, mohou mít různé preference spoření, což ovlivní růst čistého bohatství.
Kdy má kvantilová regrese význam
Předpokládejme, že máme jednoduchý model
E
(y|x)=β0+xβ1
, kde yy
is the outcome variable and x
je kovariátou.
x
bere
hodnoty v {0,1,2,3,4,5,6}{
0,1,2,3,4,5,6}
. Podle definice, β1β
1
plně charakterizuje účinky zvýšení o jednu jednotku.
x
na podmíněném průměru výsledku
y
; to je,
β1=E(y|x=a+1)−E(y|x=a)
β1=E(y|x=a+1)−E(y|x=a)
. Níže uvádíme
dva scénáře procesu generování dat.
1. Pouze posunutá poloha. Funkce hustoty pravděpodobnosti podmíněného výsledku
na
x=a+1
f(y|x=a+1)
f(y|x=a+1)
, je pouze relativně posunutá.
vůči
f(y|x=a)
f(y|x=a)
. V tomto případě,
β1
β1
shrnuje vliv
x
nejen na podmíněném průměru, ale také na každém podmíněném kvantilu.
na
y
y
. Tento případ je znázorněn na levém panelu obrázku 1.
2. Poloha posunutá a přeškálovaná. Funkce hustoty pravděpodobnosti výsledku podmíněná na
x=a+1
x=a+1
,
f(y|x=a+1)
f(y|x=a+1)
, je posunutá a přeškálovaná vzhledem k poloze.
f(y|x=a)
.V tomto případě,
β1
shrnuje vliv
x
pouze na základě podmínky
ale ne na podmíněných kvantilech y
y
. Tento případ je znázorněn v
na pravém panelu obrázku 1.
Obrázek 1
Na levém panelu vidíme, že každá podmíněná hustota je vzhledem k ostatním paralelní; posunuta byla pouze poloha. V tomto případě
β1
β1
zachycuje posun jak podmíněného průměru, tak všech dalších podmíněných kvantilů výsledku. V důsledku toho poskytuje lineární regrese tolik informací o
β1
jako kvantilovou regresi.
Naproti tomu v pravém panelu je podmíněná hustota pro každou hladinu
x
má jiné umístění a jiný tvar. Tedy,
β1
lze shrnout posuny podmíněných průměrů, které se obecně liší od posunů podmíněných kvantilů. Kvantilová regrese se stává nezbytnou pro poznání účinků
x
na podmíněných kvantilech výsledku.
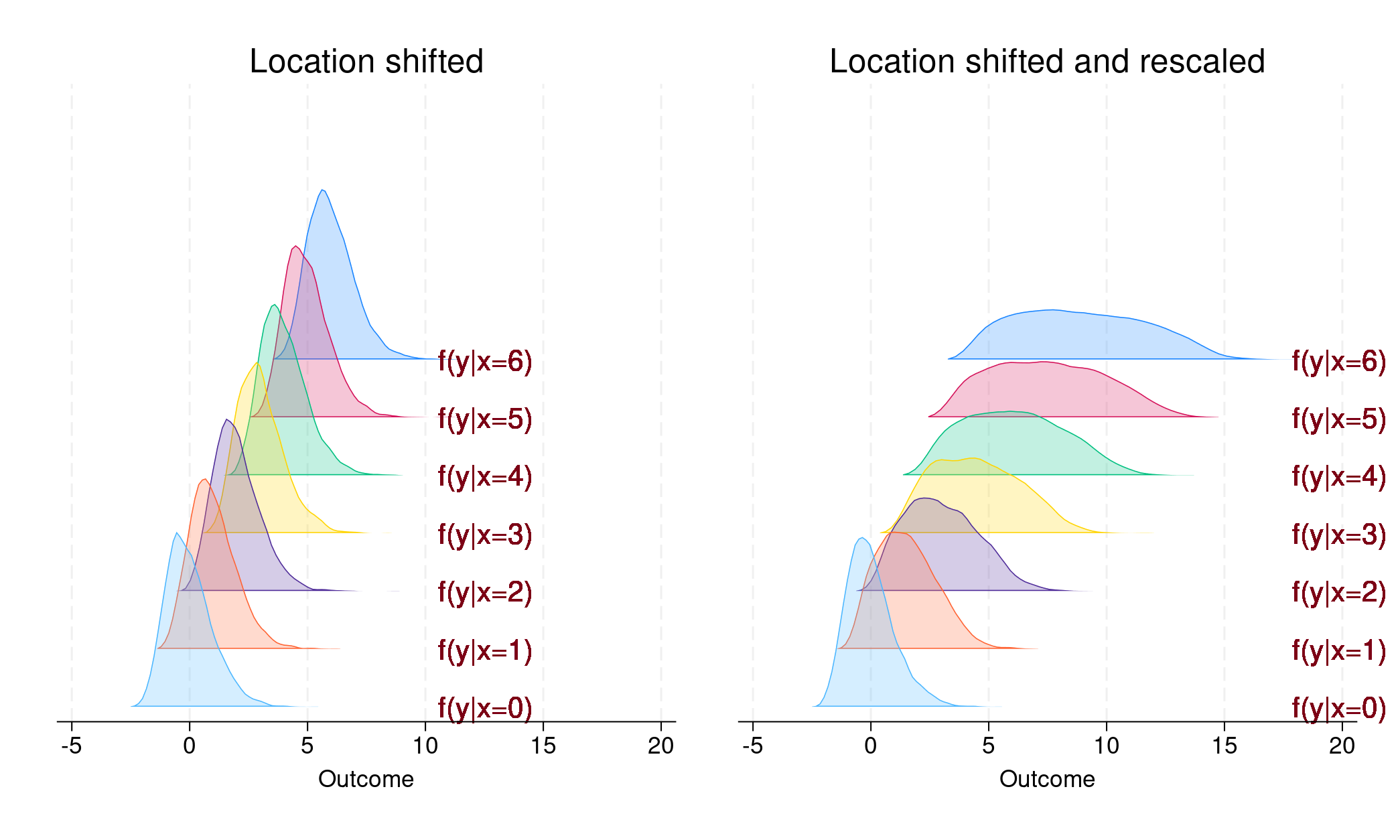
Na levém panelu vidíme, že každá podmíněná hustota je vůči ostatním paralelní, pouze umístění bylo posunuto. V tomto případě je β1
�1
zachycuje posun jak podmíněného průměru, tak všech dalších podmíněných kvantilů výsledku. V důsledku toho poskytuje lineární regrese tolik informací o β1
�1
jako kvantilovou regresi.
Naproti tomu v pravém panelu je podmíněná hustota pro každou úroveň x
�
má jiné umístění a jiný tvar. Proto β1
�1
lze shrnout posuny podmíněných průměrů, které se obecně liší od posunů podmíněných kvantilů. Kvantilová regrese se stává nezbytnou pro poznání vlivu x
�
na podmíněných kvantilech výsledku.
Podívejme se, jak to funguje
Chceme odhadnout vliv účasti v systému 401(k) (p401k) na různé podmíněné kvantily čistých finančních aktiv (aktiv). Používáme údaje, které uvádějí Chernozhukov a Hansen (2004). Tato data pocházejí ze vzorku domácností z šetření Survey of Income and Program Participation (SIPP) z roku 1990. U hlavy domácnosti máme k dispozici údaje o příjmu (income), věku (age), počtu osob v rodině (familysize), rodinném stavu (married), účasti na IRA (ira), účasti na důchodovém zabezpečení (pension), vlastnictví domu (ownhome) a letech vzdělání (educ).
Domníváme se, že účast v programu 401(k) je endogenní, protože může záviset na nepozorovaných faktorech, jako jsou preference spoření, které rovněž ovlivňují finanční aktiva. Jako nástroj pro účast v programu 401(k) použijeme způsobilost k účasti v programu 401(k) (e401k).
K odhadu vlivu účasti v systému 401(k) na podmíněný medián (výchozí hodnotu) čistých finančních aktiv použijeme odhad IQR (ivqregress iqr).
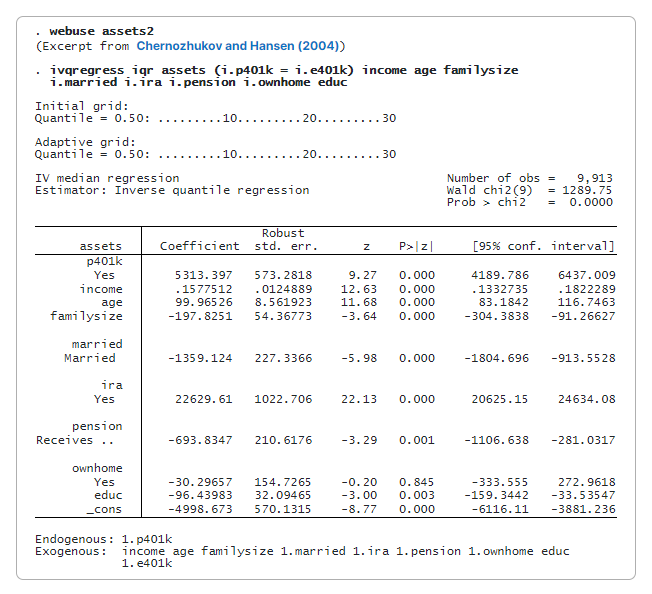
Koeficient pro p401k je 5,313. To znamená, že účast v systému 401(k) by zvýšila medián čistých finančních aktiv o 5 313 USD, podmíněný ostatními kovariátami, ve srovnání se scénářem, kdy se nikdo neúčastní.
Po ivqregress iqr můžeme použít estat dualci k získání duálního intervalu spolehlivosti (CI), který je robustní vůči slabým instrumentům pro koeficient endogenních proměnných.
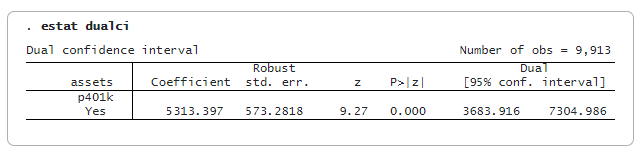
Duální CI je obvykle širší než běžný CI; poskytuje robustnější inferenci, pokud jsou nástroje slabé. Zde je duální 95% CI [3684, 7305], což je širší než běžný 95% CI [4190, 6437].
Odhadli jsme vliv ošetření účasti v programu 401(k) (p401k) na podmíněný medián čistých finančních aktiv (aktiv). Z hlediska tvůrce politiky nás však může více zajímat odhad ošetřovacího efektu p401k na jiné podmíněné kvantily aktiv.
Tentokrát zadáme ivqregress smooth, abychom použili odhad vyhlazených odhadních rovnic pro fitování modelu na různých kvantilech. Konkrétně zadáme možnost quantile(10(10)90), abychom model IVQR přizpůsobili na 10., 20., . . , 90. kvantilu.
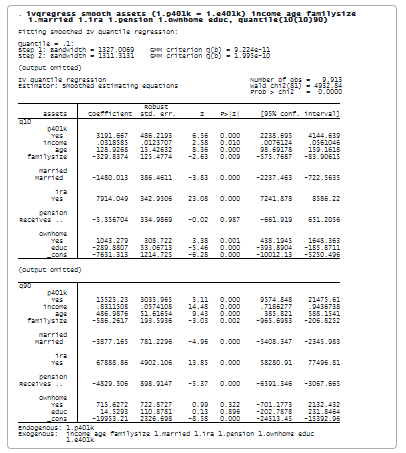
Výsledky ukazují odhady vlivu účasti v programu 401(k) na každý podmíněný kvantil aktiva. Interpretace koeficientů je podobná jako dříve, jen s tím rozdílem, že se díváme na různé podmíněné kvantily. Například pro kvantil q90 je odhad koeficientu pro p401k 15,525. Účast v programu 401(k) by tedy zvýšila 90% podmíněný kvantil čistých finančních aktiv o 15 525 USD.
Kromě toho, že se podíváme na přesné číselné odhady z tabulky koeficientů, můžeme použít estat coefplot k vizualizaci efektu ošetření p401k od dolního k hornímu kvantilu.
. estat coefplot
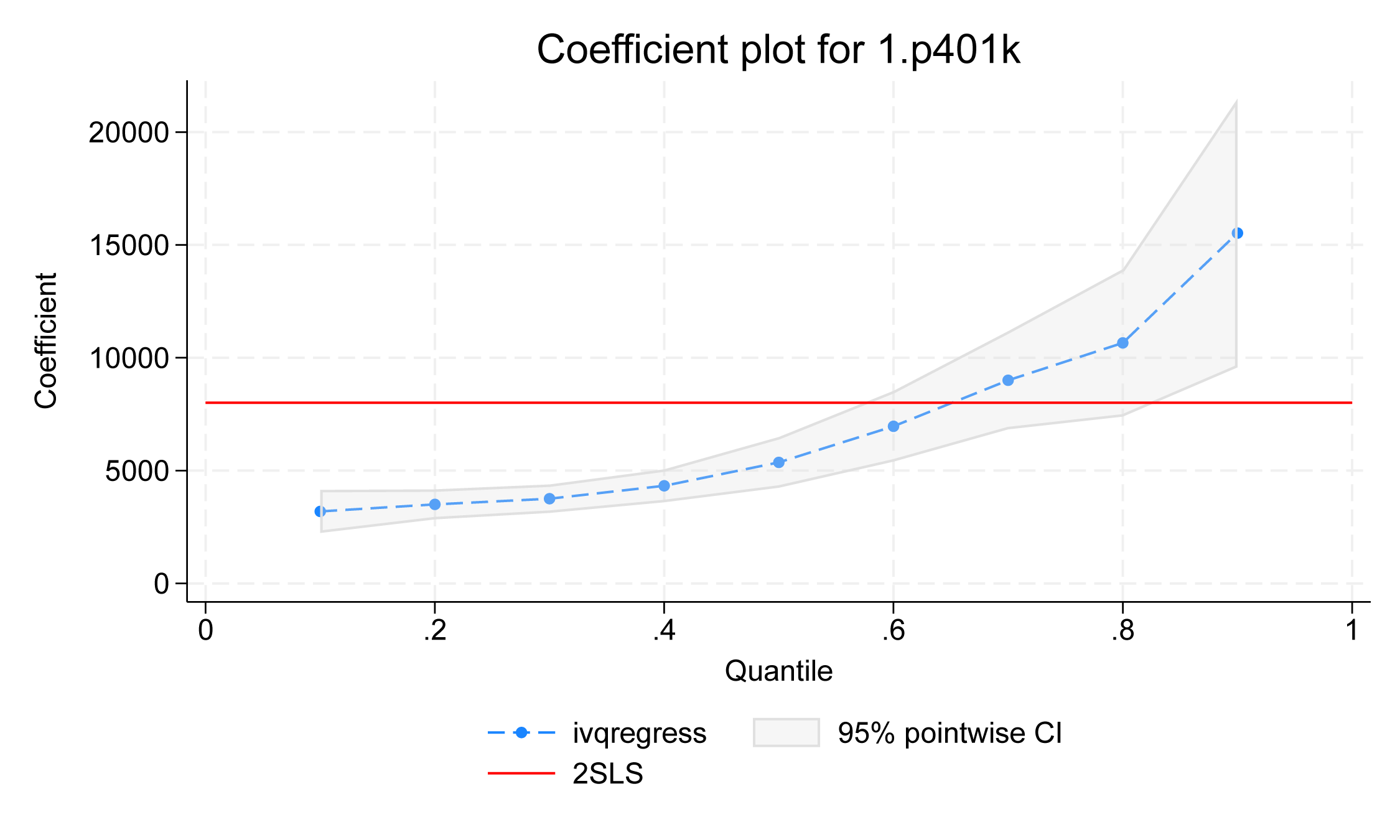
Obrázek 2
Tečky v grafu znázorňují bodové odhady léčebného účinku p401k na různé podmíněné kvantily aktiv a šedá hranice znázorňuje 95% bodové CI. Vidíme vzestupný trend léčebného účinku p401k. U kvantilů nižších úrovní, jako jsou 10., 20., 30. a 40. kvantil, je léčebný efekt relativně plochý. Účinek léčby se však zvyšuje v kvantilech vyšší úrovně. Červená čára ukazuje dvoustupňové odhady metodou nejmenších čtverců, které lze použít jako referenční hodnotu.
Pomocí estat endogeffects můžeme testovat následující hypotézy týkající se endogenní kovariáty:
-
Bez vlivu : Účast v systému 401(k) nemá vliv na čistá finanční aktiva pro všechny odhadované kvantily.
-
Konstantní účinek : Účinek účasti v programu 401(k) je konstantní pro všechny odhadované kvantily.
-
Dominance : Účast v programu 401(k) je jednoznačně pozitivní pro všechny odhadované kvantily; to znamená, že hodnoty koeficientů jsou striktně kladné.
-
Exogenita : Účast v programu 401(k) je exogenní.
Pro zobrazení Kolmogorovovy-Smirnovovy statistiky a 95% kritické hodnoty pro každou hypotézu používáme estat endogeffects. Nulovou hypotézu můžeme zamítnout, pokud je testovací statistika větší než kritická hodnota; v opačném případě nulovou hypotézu nemůžeme zamítnout. Zadáme volbu rseed(), aby byly výsledky reprodukovatelné, protože kritické hodnoty jsou generovány z bootstrapového vzorku.
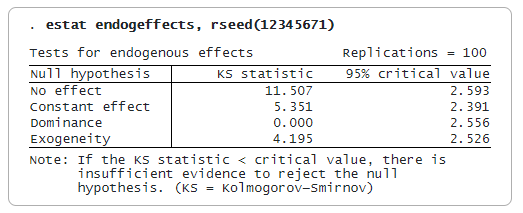
Zjistili jsme, že účast v systému 401(k) má určitý vliv, že zacházení není konstantní v různých kvantilech a že účast v systému 401(k) je endogenní. Test dominance ukazuje, že účast v programu 401(k) je jednoznačně výhodná pro všechna odhadovaná kvantily aktiv.
Výsledky testu jsou v souladu s grafem koeficientů vytvořeným pomocí estat coefplot, kde jsme viděli, že účinky ošetření jsou kladné (hypotézy dominance a žádného účinku) a mají vzestupnou tendenci (hypotéza konstantního účinku).
Odkaz
Chernozhukov, V. a C. Hansen. 2004. The effects of 401(k) participation on the wealth distribution (Dopady účasti v systému 401(k) na rozdělení bohatství): Vliv kvantilové regresní analýzy na majetkové poměry. Review of Economics and Statistics 86: 735-751.

