New In 
Regresia cuantică a variabilelor instrumentale
Regresia cuantilă cu variabile instrumentaleCând dorim să studiem efectele covariatelor asupra diferitelor cuante ale rezultatului, folosim regresia cuantilă. Dar ce se întâmplă dacă bănuim că o covariantă este endogenă? Noua comandă ivqregress modelează cuantele rezultatului și, în același timp, controlează problemele care apar din cauza endogeneității.
Repere
-
Estimatori cantitativi ai variabilelor instrumentale (IV)
-
Regresie cuantică inversă (IQR)
-
Ecuații de estimare netezite
-
-
Estimatorul IQR
-
Intervale de încredere robuste la instrumente slabe
-
Diagnosticarea grafică a convergenței
-
-
Estimare simultană pe cuante
-
Vizualizarea efectelor pe cuante
-
Teste specializate
-
IV care nu afectează rezultatul
-
Egalitatea efectelor endogene între quantiles
-
Efecte mai mari decât zero în toate cuantele
-
IV fiind exogenă în loc de endogenă
-
Prezentare generală
Atunci când folosim regresia liniară, modelăm media rezultatului. Cu toate acestea, uneori, am dori să studiem alte caracteristici ale distribuției rezultatelor decât media. De exemplu, un responsabil politic ar putea dori să afle cum ar afecta participarea la un plan de pensionare 401(k) cuantele condiționate de nivel inferior, median și superior ale averii nete.
ivqregress estimează parametrii la cuantele distribuției rezultatelor și ține cont de problemele de endogeneitate care apar din motive precum auto-selecția, omiterea unei variabile relevante sau eroarea de măsurare. De exemplu, participarea la programul 401(k) poate fi endogenă, deoarece persoanele care participă și cele care nu participă pot avea preferințe de economisire diferite, ceea ce va afecta creșterea bogăției nete.
Când contează regresia cuantilelor
Să presupunem că avem un model simplu
E
(y|x)=β0+xβ1
, unde
y
y
este variabila de rezultat și
x
este o covariabilă.
x
x
ia
valori în
{0,1,2,3,4,5,6}{
0,1,2,3,4,5,6}
. Prin definiție,
β
1
β
1
caracterizează pe deplin efectele creșterii unei unități de
x
x
pe media condiționată a rezultatului
y
y
; adică,
β1=E(y|x=a+1)−E(y|x=a)
β1=E(y|x=a+1)−E(y|x=a)
. Mai jos, vom
luăm în considerare două scenarii ale procesului de generare a datelor.
1. Doar locația schimbată. Funcția de densitate de probabilitate a rezultatului condițional
la
x=a+1
x=a+1
f(y|x=a+1)
f(y|x=a+1)
, este doar deplasată în raport cu locația
față de
f(y|x=a)
f(y|x=a)
. În acest caz,
β
1
β1
sintetizează efectul
x
x
nu numai pe media condiționată, ci și pe fiecare cupolă condiționată
din
y
y
. Acest caz este ilustrat în panoul din stânga din figura 1.
2. Locația deplasată și redimensionată. Funcția de densitate de probabilitate a rezultatului condiționată de
x=a+1
x=a+1
,
f(y|x=a+1)
f(y|x=a+1)
, este atât deplasată și redimensionată în raport cu
f(y|x=a)
f(y|x=a)
.
În acest caz,
β
1
β1
sintetizează efectul
x
x
numai pe baza condiției
medie, dar nu și pe cuantele condiționate ale
y
y
. Acest caz este ilustrat în
panoul din dreapta din figura 1.
În panoul din stânga, observăm că fiecare densitate condiționată este paralelă în raport cu celelalte; doar locația a fost schimbată. În acest caz,
β1
β1
surprinde schimbarea atât a mediei condiționate, cât și a oricăror alte cuantile condiționate ale rezultatului. Prin urmare, rularea unei regresii liniare oferă la fel de multe informații despre
β
1
β1
sub forma unei regresii cuantice.
În schimb, în panoul din dreapta, densitatea condiționată pentru fiecare nivel de
x
x
are o locație diferită și o formă diferită. Astfel,
β1
β1
poate rezuma modificările mediei condiționate, care, în general, diferă de modificările cuantelor condiționate. Regresia cuantică devine necesară pentru a afla despre efectele
x
x
cu privire la cuantele condiționate ale rezultatului.
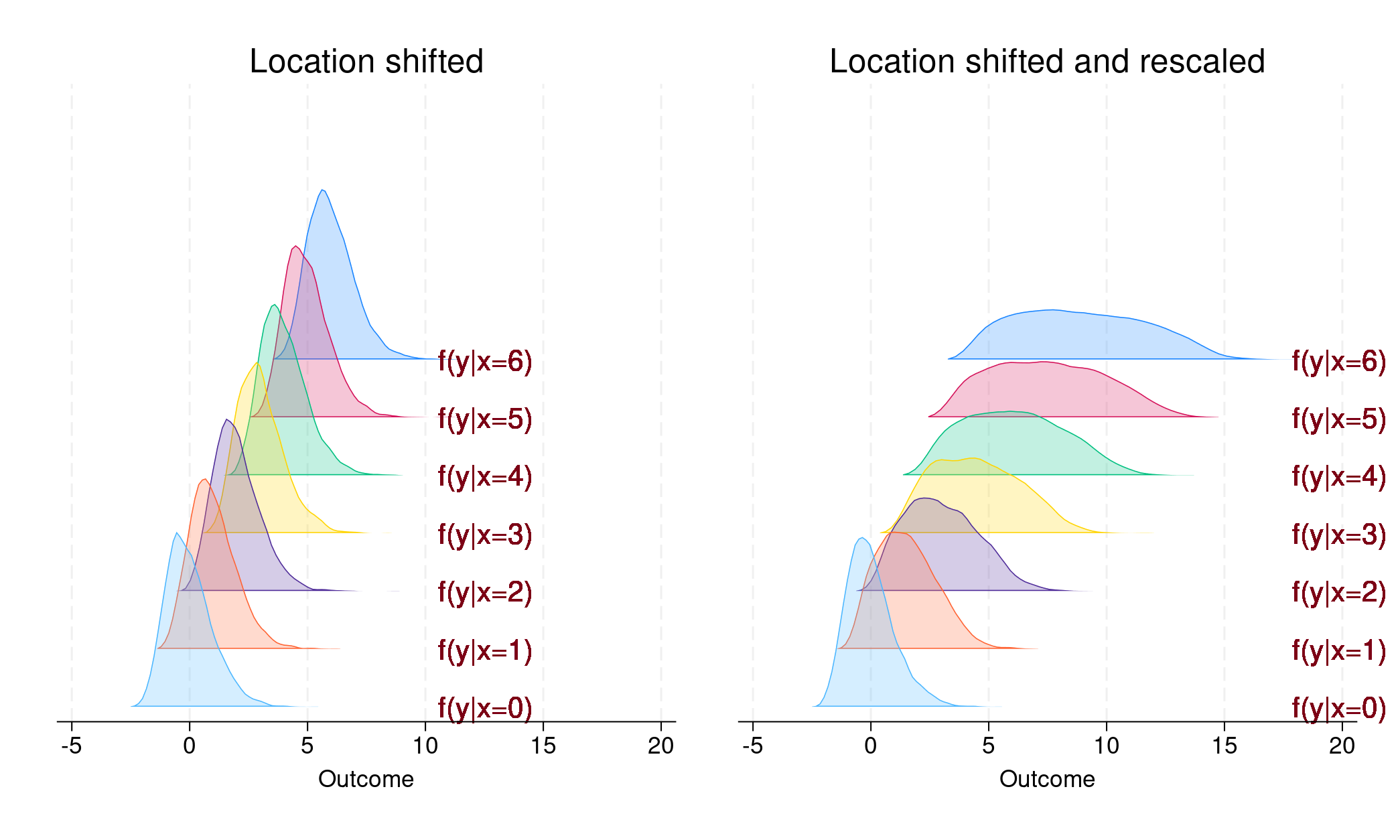
În panoul din stânga, observăm că fiecare densitate condiționată este paralelă în raport cu celelalte; doar locația a fost schimbată. În acest caz, β1
�1
surprinde schimbarea atât a mediei condiționate, cât și a oricăror alte cuantile condiționate ale rezultatului. Prin urmare, efectuarea unei regresii liniare oferă la fel de multe informații despre β1
�1
sub forma unei regresii cuantice.
În schimb, în panoul din dreapta, densitatea condiționată pentru fiecare nivel al lui x
�
are o locație diferită și o formă diferită. Astfel, β1
�1
poate rezuma modificările mediei condiționate, care, în general, diferă de modificările cuantelor condiționate. Regresia cuantică devine necesară pentru a afla despre efectele lui x
�
cu privire la cuantele condiționate ale rezultatului.
Să vedem cum funcționează
Dorim să estimăm efectul participării la 401(k) (p401k) asupra diferitelor cuante condiționate ale activelor financiare nete (active). Utilizăm datele raportate de Chernozhukov și Hansen (2004). Aceste date provin dintr-un eșantion de gospodării din cadrul Survey of Income and Program Participation (SIPP) din 1990. Pentru capul gospodăriei, dispunem de date privind venitul (income), vârsta (age), numărul de persoane din familie (familysize), starea civilă (married), participarea la IRA (ira), participarea la beneficii de pensie (pension), proprietatea asupra locuinței (ownhome) și anii de educație (educ).
Suspectăm că participarea la 401(k) este endogenă, deoarece poate depinde de factori neobservați, cum ar fi preferința de economisire, care afectează, de asemenea, activele financiare. Vom utiliza eligibilitatea 401(k) (e401k) ca instrument pentru participarea la 401(k).
Utilizăm estimatorul IQR (ivqregress iqr) pentru a estima efectul participării la 401(k) asupra medianei condiționate (implicit) a activelor financiare nete.
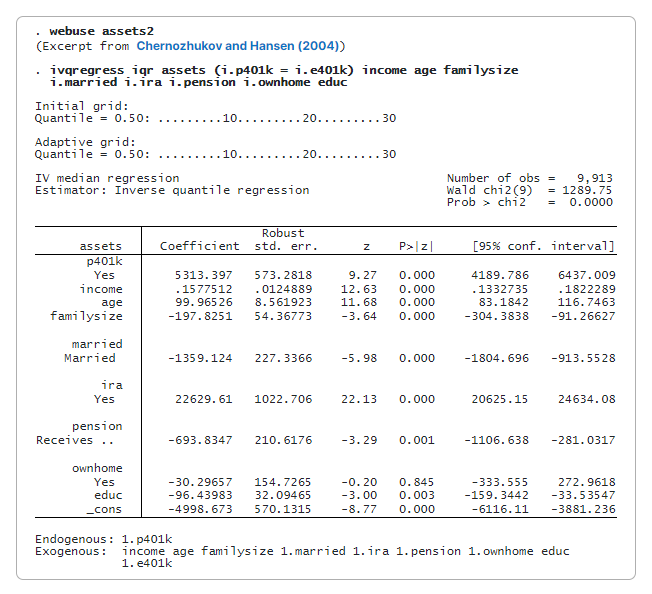
Coeficientul pentru p401k este 5,313. Aceasta înseamnă că participarea la un program 401(k) ar crește activele financiare nete mediane cu 5.313 USD, în funcție de alte covariate, în raport cu un scenariu în care nimeni nu participă.
După ivqregress iqr, putem utiliza estat dualci pentru a obține intervalul de încredere (IC) dual care este robust la instrumente slabe pentru coeficientul variabilelor endogene.
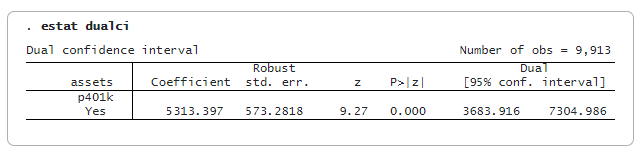
IC dublu este de obicei mai larg decât IC obișnuit; acesta oferă o inferență mai robustă în cazul în care instrumentele sunt slabe. În acest caz, IC dublu de 95% este [3684, 7305], care este mai larg decât IC obișnuit de 95% [4190, 6437].
Am estimat efectul tratamentului participării la 401(k) (p401k) asupra medianei condiționate a activelor financiare nete (active). Cu toate acestea, din punctul de vedere al elaboratorului de politici, am putea fi mai interesați să estimăm efectul tratamentului p401k asupra altor cuante condiționate ale activelor.
De data aceasta, specificăm ivqregress smooth pentru a utiliza estimatorul de ecuații de estimare netezite pentru a ajusta modelul la diferite cuantile. În special, specificăm opțiunea quantile(10(10)90) pentru a potrivi modelul IVQR la al 10-lea, al 20-lea, . . . . , 90 cuantiles.
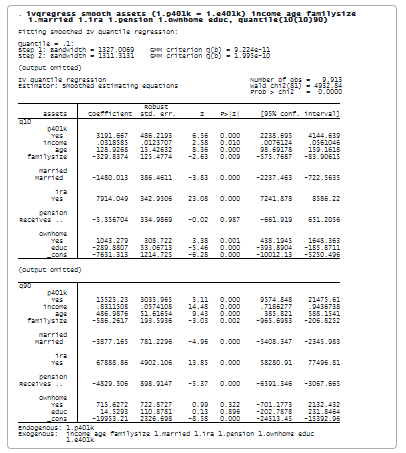
Rezultatele arată estimările pentru efectul participării la 401(k) asupra fiecărui cuantile condițional al activului. Interpretarea coeficienților este similară cu cea anterioară, cu excepția faptului că avem în vedere diferite cuante condiționate. De exemplu, pentru cuantila q90, estimarea coeficientului pentru p401k este de 15,525. Astfel, participarea la 401(k) ar crește cu 15.525 $ cuantumul condiționat 90% al activelor financiare nete.
Pe lângă examinarea estimărilor numerice exacte din tabelul de coeficienți, putem utiliza estat coefplot pentru a vizualiza efectul de tratament al p401k de la cuantilă inferioară la cea superioară.
. estat coefplot
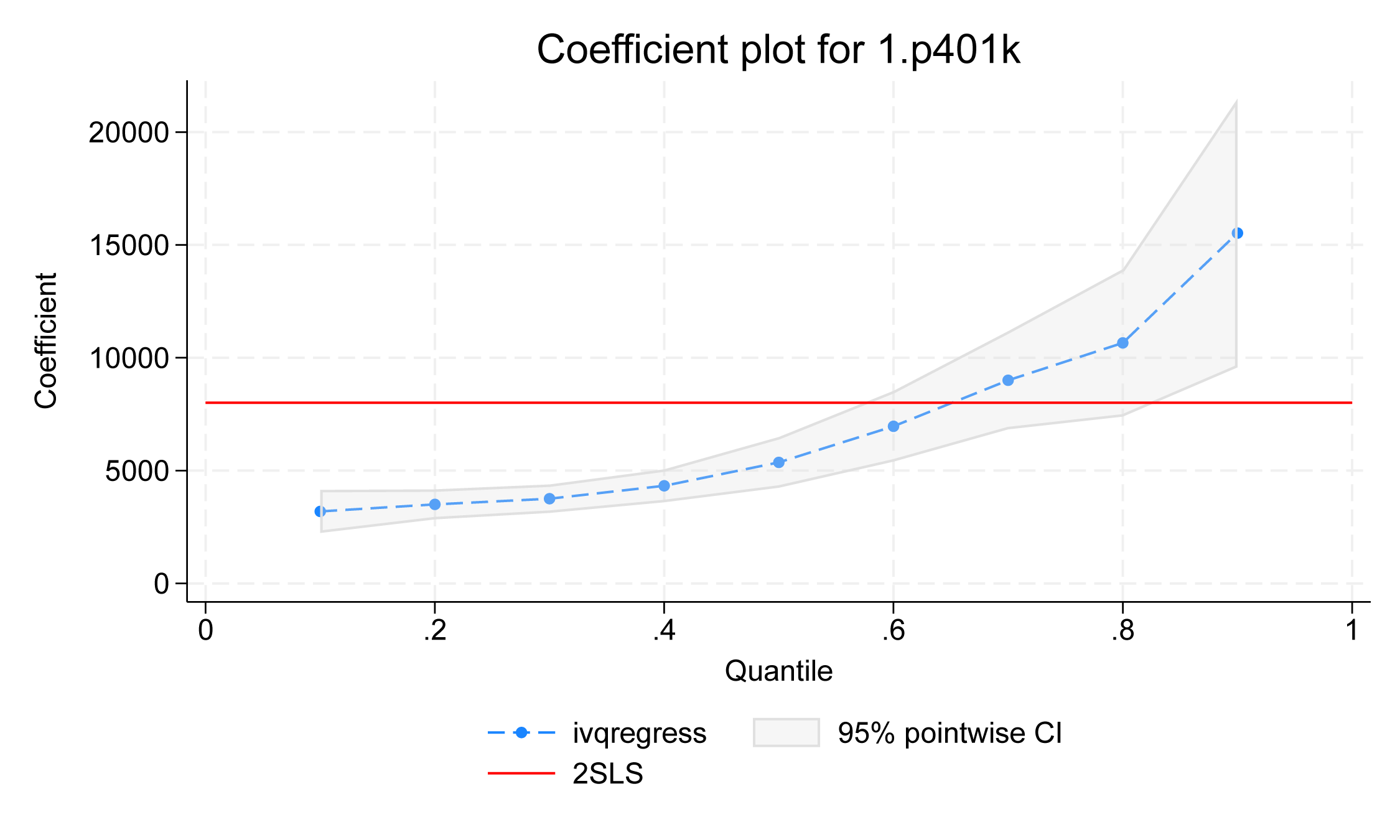
Figure 2
Punctele din grafic arată estimările punctuale ale efectului tratamentului p401k asupra diferitelor cuante condiționate ale activelor, iar limita gri arată IC-ul punctual de 95%. Observăm o tendință ascendentă a efectului de tratament al p401k. La cuantele de nivel inferior, cum ar fi a 10-a, a 20-a, a 30-a și a 40-a cuante, efectul tratamentului este relativ plat. Cu toate acestea, efectul tratamentului crește în cuantele de nivel superior. Linia roșie prezintă estimările în două etape ale celor mai mici pătrate, care pot fi utilizate ca punct de referință.
Putem utiliza estat endogeffects pentru a testa următoarele ipoteze cu privire la covariabila endogenă:
-
Nici un efect: Participarea la 401(k) nu afectează activele financiare nete pentru toate cuantele estimate.
-
Efect constant: Efectul de tratament al participării la 401(k) este constant pentru toate cuantele estimate.
-
Dominanță : Participarea la 401(k) este în mod clar pozitivă pentru toate cuantele estimate; adică valorile coeficienților sunt strict pozitive.
-
Exogenitate : Participarea la 401(k) este exogenă.
Folosim estat endogeffects pentru a arăta statistica Kolmogorov-Smirnov și valoarea critică de 95% pentru fiecare ipoteză. Putem respinge ipoteza nulă dacă statistica de testare este mai mare decât valoarea critică; în caz contrar, nu putem respinge ipoteza nulă. Specificăm opțiunea rseed() pentru ca rezultatele să fie reproductibile, deoarece valorile critice sunt generate dintr-un eșantion bootstrap.
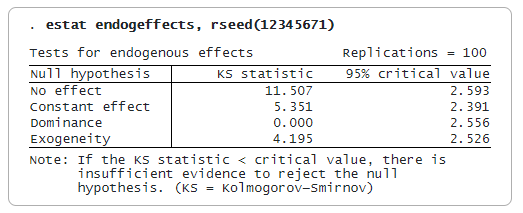
Constatăm că participarea la 401(k) are un anumit efect, că tratamentul nu este constant între diferite cuante și că participarea la 401(k) este endogenă. Testul de dominanță indică faptul că participarea la 401(k) este fără echivoc benefică pentru toate cuantele de active estimate.
Rezultatele testului sunt în concordanță cu graficul coeficienților produs de estat coefplot, unde am văzut că efectele tratamentului sunt pozitive (ipoteza dominanței și ipoteza lipsei de efect) și au o tendință ascendentă (ipoteza efectului constant).
Referință
Chernozhukov, V., și C. Hansen. 2004. Efectele participării la 401(k) asupra distribuției bogăției: O analiză instrumentală de regresie cuantilativă. Review of Economics and Statistics 86: 735-751.

