Régression quantile IV

New In

Régression quantile à variables instrumentales

Lorsque nous voulons étudier les effets des covariables sur différents quantiles du résultat, nous utilisons la régression des quantiles. Mais que faire si nous soupçonnons qu’une covariable est endogène ? La nouvelle commande ivqregress modélise les quantiles du résultat et, en même temps, contrôle les problèmes liés à l’endogénéité.

-> Vue d’ensemble -> Quand la régression par quantile est importante -> Voyons comment cela fonctionne -> Référence

Points forts

Estimateurs de variables instrumentales (IV) par quantile
- Régression quantile inverse (IQR)
- Équations d’estimation lissées
Estimateur IQR
- Intervalles de confiance robustes en cas d’instruments faibles
- Diagnostics graphiques de convergence
Estimation simultanée sur les quantiles
Visualisation des effets sur les quantiles
Tests spécialisés
- IV n’affectant pas le résultat
- Égalité des effets endogènes entre les quantiles
- Effets supérieurs à zéro entre les quantiles
- IV exogène au lieu d’endogène

Vue d’ensemble

Lorsque nous utilisons la régression linéaire, nous modélisons la moyenne du résultat. Or, il arrive que nous souhaitions étudier des caractéristiques de la distribution des résultats autres que la moyenne. Par exemple, un décideur politique peut vouloir savoir comment la participation à un plan de retraite 401(k) affecterait les quantiles conditionnels inférieurs, médians et supérieurs de la richesse nette.

ivqregress estime les paramètres aux quantiles de la distribution des résultats et tient compte des problèmes d’endogénéité qui surviennent pour des raisons telles que l’autosélection, l’omission d’une variable pertinente ou l’erreur de mesure. Par exemple, la participation au programme 401(k) peut être endogène parce que les personnes qui y participent et celles qui n’y participent pas peuvent avoir des préférences différentes en matière d’épargne, ce qui affectera la croissance de la richesse nette.

Quand la régression par quantile est importante

Supposons que nous ayons un modèle simple
E

(y|x)=β0+xβ1

$// <![CDATA[ E(y|x) = \beta_0 + x\beta_1 // ]]>$

où
y

$// <![CDATA[ y // ]]>$

est la variable de résultat et

$// <![CDATA[ x // ]]>$

est une covariable.
x

$// <![CDATA[ x // ]]>$

prend
prend des valeurs en
${0, 1, 2, 3, 4, 5, 6}$

0,1,2,3,4,5,6}

$// <![CDATA[ \{0, 1, 2, 3, 4, 5, 6\} // ]]>$

. Par définition, $β_{1}$

$// <![CDATA[ \beta_1 // ]]>$

caractérise pleinement les effets de l’augmentation d’une unité de
x

$// <![CDATA[ x // ]]>$

sur la moyenne conditionnelle du résultat
y

$// <![CDATA[ y // ]]>$

; c’est-à-dire, $β_{1} = E (y | x = a + 1) - E (y | x = a)$

β1=E(y|x=a+1)−E(y|x=a)

$// <![CDATA[ \beta_1 = E(y|x=a + 1) - E(y|x=a) // ]]>$

. Ci-dessous, nous
deux scénarios du processus de génération des données.

1. Emplacement décalé uniquement. La fonction de densité de probabilité du résultat conditionnel
sur

x=a+1

$f (y | x = a + 1)$

f(y|x=a+1)

$// <![CDATA[ f(y|x=a+1) // ]]>$

est seulement décalé par rapport à l’endroit où il se trouve.
par rapport $f (y | x = a)$

f(y|x=a)

$// <![CDATA[ f(y|x=a) // ]]>$

. Dans ce cas,

β1

$// <![CDATA[ \beta_1 // ]]>$

résume l’effet de

$// <![CDATA[ x // ]]>$

non seulement sur la moyenne conditionnelle mais aussi sur chaque quantile conditionnel
de $y$

$// <![CDATA[ y // ]]>$

. Ce cas est illustré dans le panneau gauche de la figure 1.

2. Emplacement décalé et rééchelonné. La fonction de densité de probabilité du résultat conditionnel à

$x = a + 1$

x=a+1

$// <![CDATA[ x=a+1 // ]]>$

,
$f (y | x = a + 1)$

f(y|x=a+1)

$// <![CDATA[ f(y|x=a+1) // ]]>$

est à la fois décalée et remise à l’échelle par rapport à

f(y|x=a)

$// <![CDATA[ f(y|x=a) // ]]>$

.
En l’occurrence,
$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

résume l’effet de

$// <![CDATA[ x // ]]>$

que sur la moyenne conditionnelle, mais pas sur les quantiles conditionnels.
mais pas sur les quantiles conditionnels des $y$

$// <![CDATA[ y // ]]>$

. Ce cas est illustré dans
dans le panneau de droite de la figure 1.

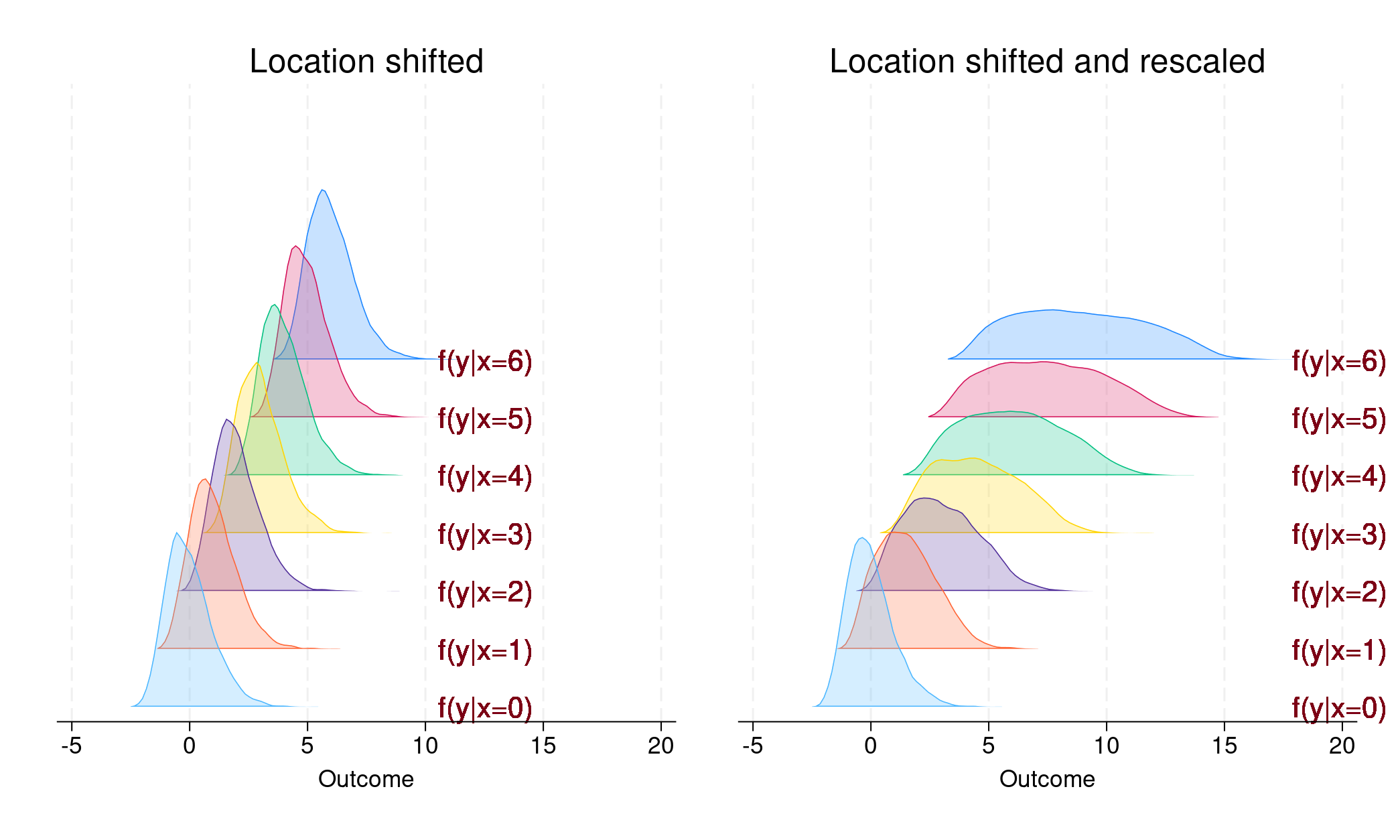
Figure 1

Dans le panneau de gauche, nous voyons que chaque densité conditionnelle est parallèle aux autres ; seul l’emplacement a été déplacé. Dans ce cas,

$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

capture le changement à la fois de la moyenne conditionnelle et de tout autre quantile conditionnel du résultat. Par conséquent, l’exécution d’une régression linéaire fournit autant d’informations sur

β1

$// <![CDATA[ \beta_1 // ]]>$

sous la forme d’une régression quantile.

En revanche, dans le panneau de droite, la densité conditionnelle pour chaque niveau de

$// <![CDATA[ x // ]]>$

a un emplacement et une forme différents. C’est pourquoi,
$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

peut résumer les déplacements de la moyenne conditionnelle, qui diffèrent généralement des déplacements des quantiles conditionnels. La régression des quantiles devient nécessaire pour connaître les effets des
$x$

$// <![CDATA[ x // ]]>$

sur les quantiles conditionnels du résultat.

$β_{1}$

comme une régression quantile.

En revanche, dans le panneau de droite, la densité conditionnelle pour chaque niveau de x

$x$

$β_{1}$

$x$

sur les quantiles conditionnels du résultat.

Voyons comment cela fonctionne

Nous voulons estimer l’effet de la participation aux plans 401(k) (p401k) sur différents quantiles conditionnels d’actifs financiers nets (actifs). Nous utilisons les données rapportées par Chernozhukov et Hansen (2004). Ces données proviennent d’un échantillon de ménages de l’Enquête sur les revenus et la participation aux programmes (SIPP) de 1990. Pour le chef de ménage, nous disposons de données sur le revenu (income), l’âge (age), le nombre de personnes dans la famille (familysize), l’état civil (married), la participation à un IRA (ira), la participation à une pension de retraite (pension), la propriété du logement (ownhome) et le nombre d’années d’études (educ).

Nous pensons que la participation au régime 401(k) est endogène car elle peut dépendre de facteurs non observés, tels que la préférence pour l’épargne, qui ont également un impact sur les actifs financiers. Nous utiliserons l’éligibilité à la 401(k) (e401k) comme instrument pour la participation à la 401(k).

Nous utilisons l’estimateur IQR (ivqregress iqr) pour estimer l’effet de la participation aux régimes 401(k) sur la médiane conditionnelle (le défaut) des actifs financiers nets.

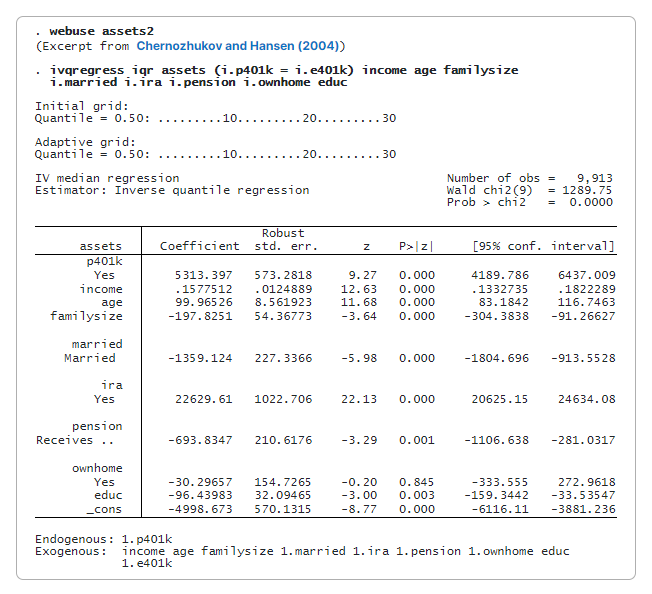
Le coefficient de p401k est de 5,313. Cela signifie que la participation à un plan 401(k) augmenterait les actifs financiers nets médians de 5 313 $, conditionnellement aux autres covariables, par rapport à un scénario où personne ne participe.

Après ivqregress iqr, nous pouvons utiliser estat dualci pour obtenir le double intervalle de confiance (IC) qui est robuste aux instruments faibles pour le coefficient des variables endogènes.

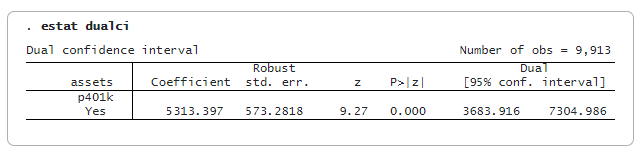
Le double IC est généralement plus large que l’IC normal ; il permet une inférence plus robuste si les instruments sont faibles. Ici, le double IC à 95 % est [3684, 7305], ce qui est plus large que l’IC à 95 % normal [4190, 6437].

Nous avons estimé l’effet de traitement de la participation aux plans 401(k) (p401k) sur la médiane conditionnelle des actifs financiers nets (actifs). Cependant, du point de vue du concepteur de la politique, il peut être plus intéressant d’estimer l’effet de traitement de p401k sur d’autres quantiles conditionnels d’actifs.

Cette fois, nous spécifions ivqregress smooth pour utiliser l’estimateur des équations d’estimation lissées afin d’ajuster le modèle à différents quantiles. En particulier, nous spécifions l’option quantile(10(10)90) pour ajuster le modèle IVQR aux 10ème, 20ème, . . . 90e quantiles.

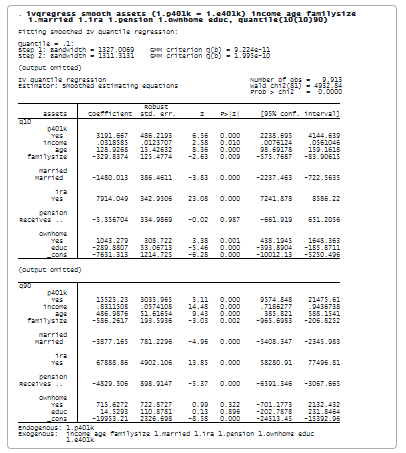
Les résultats montrent les estimations de l’effet de la participation aux régimes 401(k) sur chaque quantile conditionnel de l’actif. L’interprétation des coefficients est similaire à la précédente, sauf que nous examinons différents quantiles conditionnels. Par exemple, pour le quantile q90, l’estimation du coefficient de p401k est de 15 525. Ainsi, la participation aux régimes 401(k) augmenterait le quantile conditionnel de 90 % des actifs financiers nets de 15 525 $.

Outre l’examen des estimations numériques exactes du tableau des coefficients, nous pouvons utiliser estat coefplot pour visualiser l’effet de traitement de p401k du quantile inférieur au quantile supérieur.

. estat coefplot

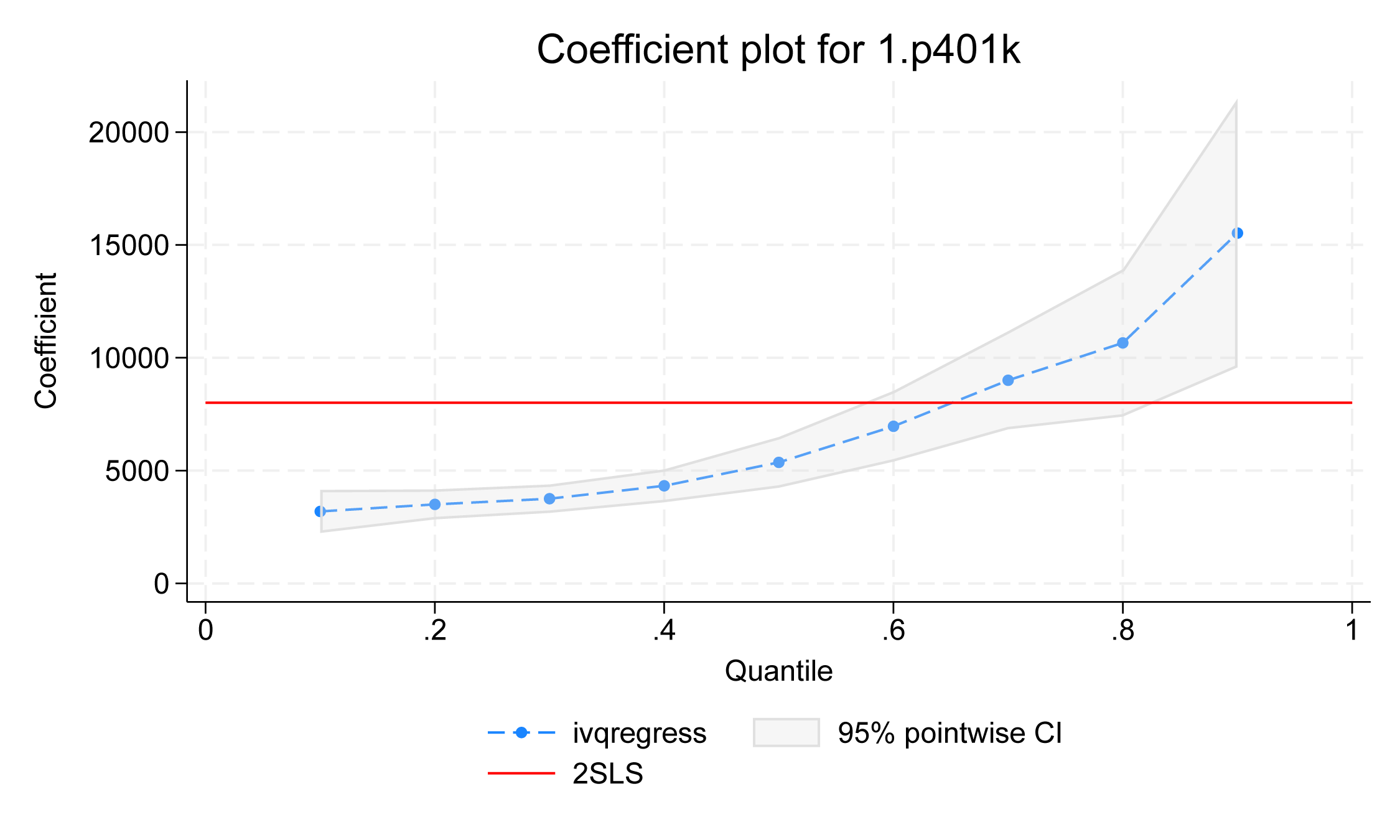
Figure 2

Les points dans le graphique montrent les estimations ponctuelles de l’effet de traitement de p401k sur différents quantiles conditionnels d’actifs, et la limite grise montre l’IC ponctuel de 95 %. Nous observons une tendance à la hausse de l’effet de traitement de p401k. Aux quantiles inférieurs, tels que les 10e, 20e, 30e et 40e quantiles, l’effet du traitement est relativement stable. Cependant, l’effet de traitement augmente dans les quantiles supérieurs. La ligne rouge montre les estimations des moindres carrés en deux étapes, qui peuvent être utilisées comme référence.

Nous pouvons utiliser les effets endogènes estat pour tester les hypothèses suivantes concernant la covariable endogène :

Aucun effet : La participation aux plans 401(k) n’affecte pas les actifs financiers nets pour tous les quantiles estimés.
Effet constant : l’effet de traitement de la participation 401(k) est constant pour tous les quantiles estimés.
Dominance : La participation 401(k) est positive sans ambiguïté pour tous les quantiles estimés ; c’est-à-dire que les valeurs des coefficients sont strictement positives.
Exogénéité : La participation 401(k) est exogène.

Nous utilisons estat endogeffects pour montrer la statistique de Kolmogorov-Smirnov et la valeur critique à 95 % pour chaque hypothèse. Nous pouvons rejeter l’hypothèse nulle si la statistique de test est supérieure à la valeur critique ; dans le cas contraire, nous ne pouvons pas rejeter l’hypothèse nulle. Nous spécifions l’option rseed() pour rendre les résultats reproductibles car les valeurs critiques sont générées à partir d’un échantillon bootstrap.

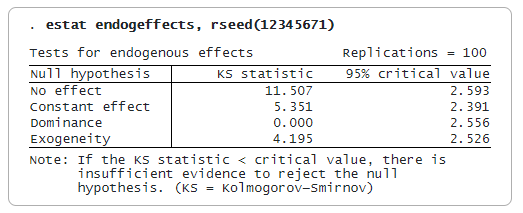
Nous constatons que la participation aux régimes 401(k) a un certain effet, que le traitement n’est pas constant entre les différents quantiles et que la participation aux régimes 401(k) est endogène. Le test de dominance indique que la participation aux plans 401(k) est sans ambiguïté bénéfique pour tous les quantiles estimés d’actifs.

Les résultats du test sont cohérents avec le graphique des coefficients produit par estat coefplot, où nous avons vu que les effets du traitement sont positifs (hypothèses de dominance et d’absence d’effet) et tendent à la hausse (hypothèse d’effet constant).

Référence

Chernozhukov, V., et C. Hansen. 2004. The effects of 401(k) participation on the wealth distribution : An instrumental quantile regression analysis. Review of Economics and Statistics 86 : 735-751.

VOIR TOUTES LES NOUVELLES FONCTIONNALITÉS

Commander Stata 18

UPGRADE