IV квантилна регресия

New In

Квантилна регресия с инструментални променливи

Когато искаме да изследваме влиянието на ковариатите върху различните квантили на резултата, използваме квантилна регресия. Но какво да правим, ако подозираме, че дадена ковариация е ендогенна? Новата команда ivqregress моделира квантилите на резултата и в същото време контролира проблемите, които възникват от ендогенността.

-> Преглед -> Кога квантовата регресия има значение -> Нека видим как работи -> Справка

Акценти

Квантилни оценки на инструментални променливи (IV)
- Обратна квантилна регресия (IQR)
- Изгладени оценъчни уравнения
IQR оценител
- Доверителни интервали, устойчиви на слаби инструменти
- Графична диагностика на конвергенцията
Едновременна оценка по квантили
Визуализация на ефектите върху квантили

Специализирани тестове
- IV не влияе на резултата
- Равнопоставеност на ендогенните ефекти в различните квантили
- Ефекти, по-големи от нула в различните квантили
- IV е екзогенен вместо ендогенен

Преглед

Когато използваме линейна регресия, моделираме средната стойност на резултата. Понякога обаче бихме искали да изследваме характеристики на разпределението на резултата, различни от средната стойност. Например един политик може да иска да научи как участието в пенсионен план 401(к) би повлияло на долните, средните и горните условни квантили на нетното богатство.

ivqregress оценява параметрите на квантилите на разпределението на резултатите и отчита проблемите с ендогенността, които възникват по причини като самоизбор, пропускане на съответната променлива или грешка при измерването. Например участието в програмата 401(k) може да бъде ендогенно, тъй като хората, които участват и които не участват, могат да имат различни предпочитания за спестяване, което ще повлияе на растежа на нетното богатство.

Кога квантовата регресия има значение

$E (y | x) = β_{0} + x β_{1}$

(y|x)=β0+xβ1

$// <![CDATA[ E(y|x) = \beta_0 + x\beta_1 // ]]>$

, където $y$ y $y$

$// <![CDATA[ y // ]]>$

$x$ $x$

$// <![CDATA[ x // ]]>$

е ковариатив. $x$ x $x$

$// <![CDATA[ x // ]]>$

взема
стойности в ${0, 1, 2, 3, 4, 5, 6}$

0,1,2,3,4,5,6}

$// <![CDATA[ \{0, 1, 2, 3, 4, 5, 6\} // ]]>$

. По дефиниция, $β_{1}$

$// <![CDATA[ \beta_1 // ]]>$

напълно характеризира ефектите от увеличаването на една единица
x
$x$

$// <![CDATA[ x // ]]>$

върху условната средна стойност на резултата
y
$y$

$// <![CDATA[ y // ]]>$

; който е, $β_{1} = E (y | x = a + 1) - E (y | x = a)$

β1=E(y|x=a+1)−E(y|x=a)

$// <![CDATA[ \beta_1 = E(y|x=a + 1) - E(y|x=a) // ]]>$

По-долу
разглеждаме два сценария на процеса на генериране на данни.

1. Само изместване на местоположението. Функцията на плътността на вероятността на условния резултат
на

x=a+1

$f (y | x = a + 1)$

f(y|x=a+1)

$// <![CDATA[ f(y|x=a+1) // ]]>$

, е само изместена спрямо местоположението
към $f (y | x = a)$

f(y|x=a)

$// <![CDATA[ f(y|x=a) // ]]>$

. В този случай, $β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

обобщава ефекта от
x

$// <![CDATA[ x // ]]>$

not only on the conditional mean but also on each conditional quantile
of $y$

$// <![CDATA[ y // ]]>$

Този случай е илюстриран в левия панел на фигура 1.

2. Изместено и премащабирано местоположение. Функцията на плътността на вероятността на резултата, обусловена от

x=a+1

$// <![CDATA[ x=a+1 // ]]>$

,
$f (y | x = a + 1)$

f(y|x=a+1)

$// <![CDATA[ f(y|x=a+1) // ]]>$

, е изместена по местоположение и преоразмерена спрямо $f (y | x = a)$

f(y|x=a)

$// <![CDATA[ f(y|x=a) // ]]>$

.
В този случай, $β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

обобщава ефекта от
x

$// <![CDATA[ x // ]]>$

само на условната
но не и върху условните квантили на $y$

$// <![CDATA[ y // ]]>$

. Този случай е илюстриран в
десния панел на Фигура 1.

Фигура 1

В левия панел се вижда, че всяка условна плътност е успоредна на останалите; изместено е само местоположението. В този случай,

β1

$// <![CDATA[ \beta_1 // ]]>$

отразява промяната както в условната средна стойност, така и във всички други условни квантили на резултата. В резултат на това провеждането на линейна регресия предоставя толкова информация за

β1

$// <![CDATA[ \beta_1 // ]]>$

като квантилна регресия.

За разлика от това, в десния панел условната плътност за всяко ниво на $x$

$// <![CDATA[ x // ]]>$

има различно местоположение и различна форма. Така, $β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

може да обобщи промените в условната средна стойност, които обикновено се различават от промените в условните квантили. Квантилната регресия става необходима, за да се научат ефектите от

$// <![CDATA[ x // ]]>$

на условните квантили на резултата.

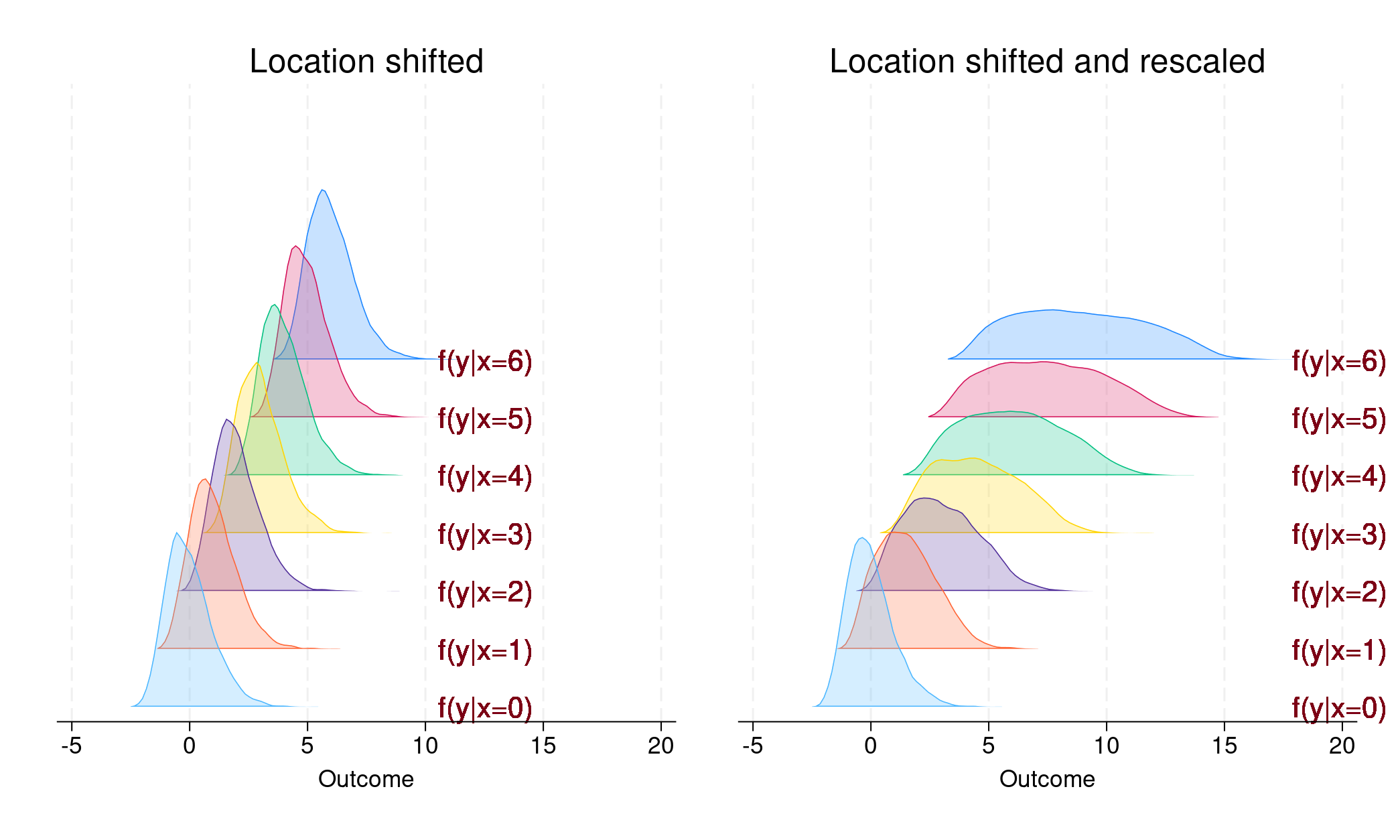
В левия панел виждаме, че всяка условна плътност е успоредна на останалите; изместено е само местоположението. В този случай β1
�1

като квантилна регресия.

За разлика от това, в десния панел условната плътност за всяко ниво на x
�

има различно местоположение и различна форма. Така β1
�1

може да обобщи промените в условната средна стойност, които обикновено се различават от промените в условните квантили. Квантилната регресия става необходима, за да научим за ефектите на x
�

върху условните квантили на резултата.

Нека видим как работи

Искаме да оценим ефекта от участието в 401(k) (p401k) върху различни условни квантили на нетните финансови активи (активи). Използваме данните, представени от Черноджуков и Хансен (2004). Тези данни са от извадка от домакинства в Изследването на доходите и участието в програми (Survey of Income and Program Participation – SIPP) от 1990 г. За главата на домакинството разполагаме с данни за доходите (income), възрастта (age), броя на хората в семейството (familysize), семейното положение (married), участието в IRA (ira), участието в пенсионно осигуряване (pension), собствеността върху жилище (ownhome) и годините на образование (educ).

Подозираме, че участието в 401(k) е ендогенно, тъй като може да зависи от ненаблюдавани фактори като предпочитания за спестяване, които също оказват влияние върху финансовите активи. Ще използваме правото на участие в 401(к) (e401k) като инструмент за участие в 401(к).

Използваме IQR оценител (ivqregress iqr), за да оценим ефекта от участието в 401(k) върху условната медиана (подразбиране) на нетните финансови активи.

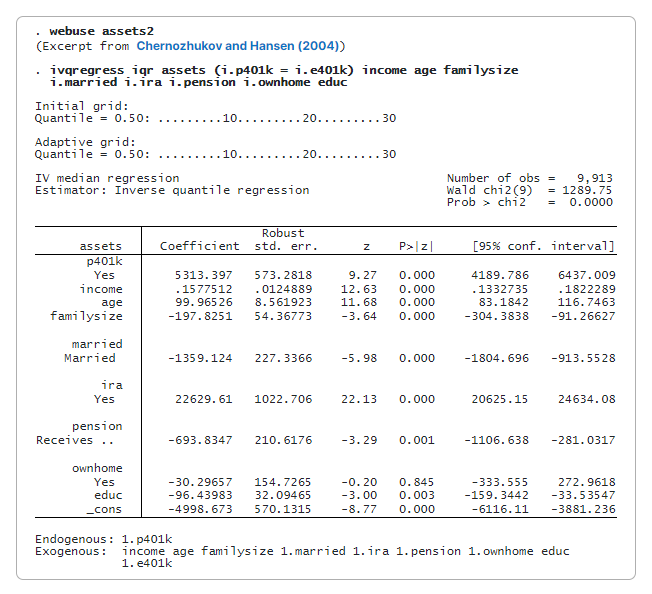
Коефициентът за p401k е 5,313. Това означава, че участието в 401(к) би увеличило медианните нетни финансови активи с 5 313 долара, при условие че има други ковариати, в сравнение със сценарий, при който никой не участва.

След ivqregress iqr можем да използваме estat dualci, за да получим двоен доверителен интервал (CI), който е устойчив на слаби инструменти за коефициента на ендогенните променливи.

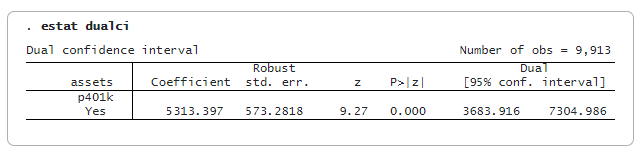
Двойният ИО обикновено е по-широк от обикновения ИО; той осигурява по-стабилни изводи, ако инструментите са слаби. В този случай двойният 95% КИ е [3684, 7305], който е по-широк от обикновения 95% КИ [4190, 6437].

Оценихме ефекта от третирането на участието в 401(k) (p401k) върху условната медиана на нетните финансови активи (активи). Въпреки това, от гледна точка на разработчика на политиката, може да сме по-заинтересовани да оценим ефекта от третирането на p401k върху други условни квантили на активите.

Този път задаваме ivqregress smooth, за да използваме оценител на изгладени оценъчни уравнения за подбиране на модела при различни квантили. По-специално, посочваме опцията quantile(10(10)90), за да подберем модела IVQR за 10-ти, 20-ти, … , 90-ия квантил.

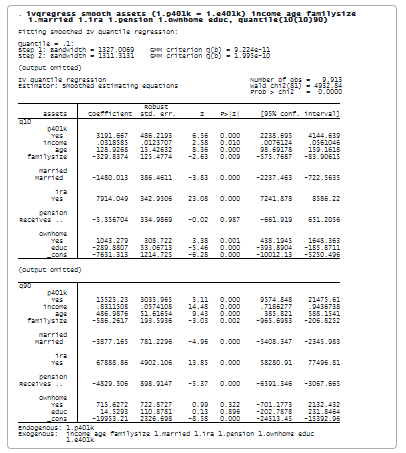
Резултатите показват оценките за ефекта от участието в 401(к) върху всеки условен квантил на актива. Интерпретацията на коефициентите е подобна на предишната, с изключение на това, че разглеждаме различни условни квантили. Например за квантил q90 оценката на коефициента за p401k е 15,525. Така участието в 401(k) ще увеличи условния квантил 90% на нетните финансови активи с 15 525 USD.

В допълнение към разглеждането на точните числови оценки от таблицата с коефициентите можем да използваме estat coefplot, за да визуализираме ефекта от третирането на p401k от долния към горния квантил.

. estat coefplot

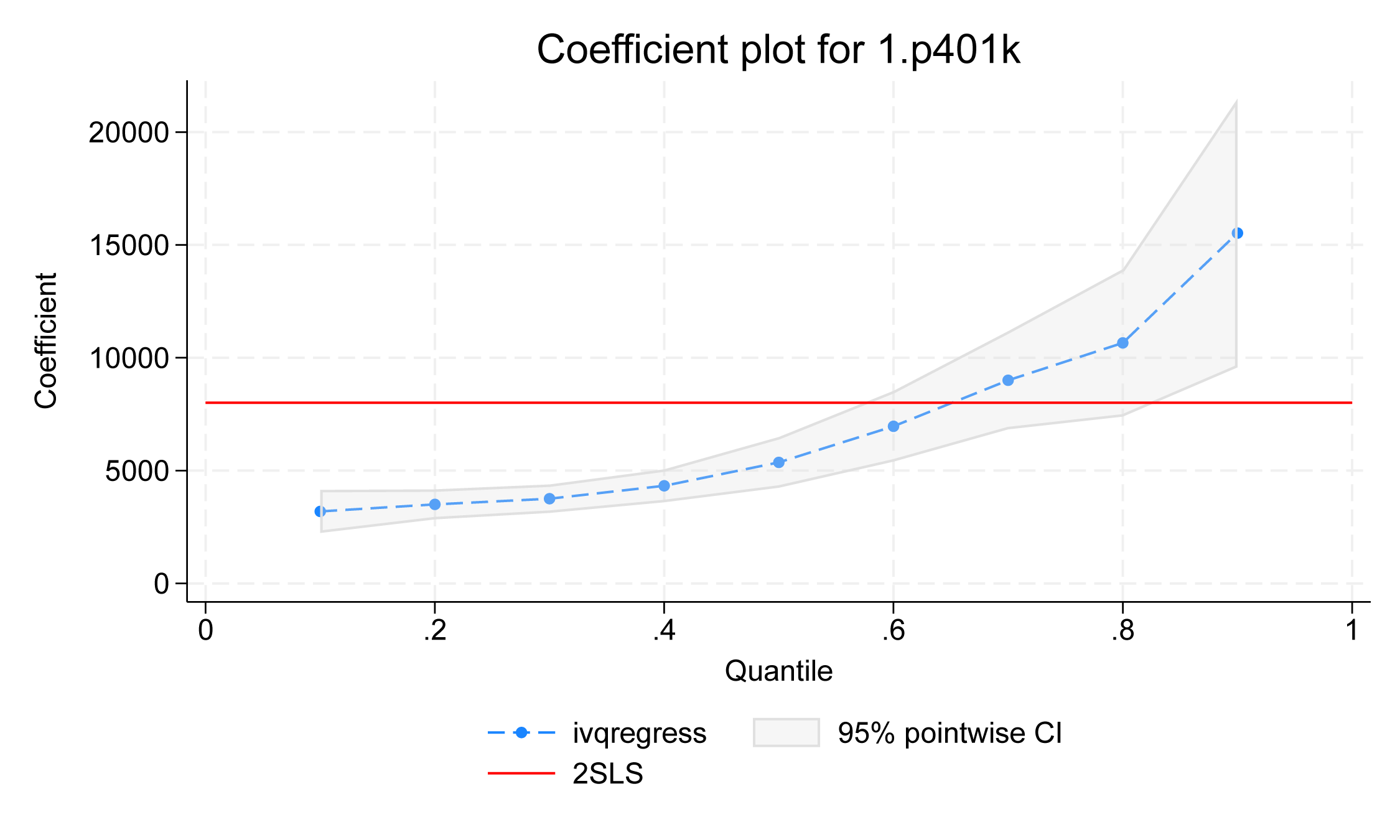
Фигура 2

Точките в графиката показват точковите оценки на ефекта от лечението с p401k върху различните условни квантили на активите, а сивата граница показва 95% точкова ДИ. Виждаме възходяща тенденция на ефекта от лечението с p401k. При по-ниските квантили, като 10-ти, 20-ти, 30-ти и 40-ти квантил, ефектът от лечението е относително плосък. Въпреки това ефектът от лечението се увеличава в горните квантили. Червената линия показва двустепенните оценки по метода на най-малките квадрати, които могат да се използват като еталон.

Можем да използваме estat endogeffects, за да проверим следните хипотези по отношение на ендогенната ковариация:

Няма ефект: Участието в 401(к) не влияе върху нетните финансови активи за всички оценени квантили.
Постоянен ефект: ефектът от третирането на участието в 401(к) е постоянен за всички оценени квантили.
Доминиране : Участието в 401(к) е недвусмислено положително за всички оценени квантили; т.е. стойностите на коефициента са строго положителни.
Екзогенност : Участието в 401(к) е екзогенно.

Използваме estat endogeffects, за да покажем статистиката на Колмогоров-Смирнов и 95% критична стойност за всяка хипотеза. Можем да отхвърлим нулевата хипотеза, ако тестовата статистика е по-голяма от критичната стойност; в противен случай не можем да отхвърлим нулевата хипотеза. Посочваме опцията rseed(), за да направим резултатите възпроизводими, тъй като критичните стойности са генерирани от bootstrap извадка.

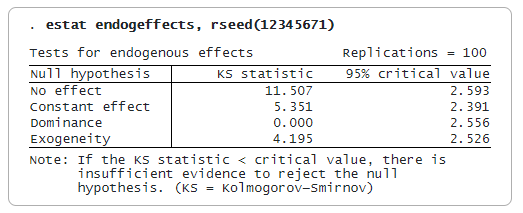
Установяваме, че участието в 401(k) има известен ефект, че третирането не е постоянно за различните квантили и че участието в 401(k) е ендогенно. Тестът за доминиране показва, че участието в 401(к) е недвусмислено благоприятно за всички оценени квантили на активите.

Резултатите от теста са в съответствие с графиката на коефициентите, изготвена от estat coefplot, където видяхме, че ефектите от третирането са положителни (хипотези за доминиране и липса на ефект) и с възходяща тенденция (хипотеза за постоянен ефект).

Справка

Черноджуков, В. и К. Хансен. 2004. Ефекти от участието в 401(к) върху разпределението на богатството: Влияние на активите на пенсионното осигуряване върху размера на пенсиите: инструментален квантилен регресионен анализ. Review of Economics and Statistics 86: 735-751.

Преглед на всички нови функции

Поръчка на Stata 18

Надграждане