New In 
Instrumental-Variablen-Quantil-Regression
Wenn wir die Auswirkungen von Kovariaten auf verschiedene Quantile des Ergebnisses untersuchen wollen, verwenden wir die Quantilsregression. Was aber, wenn wir vermuten, dass eine Kovariate endogen ist? Der neue Befehl ivqregress modelliert Quantile des Ergebnisses und kontrolliert gleichzeitig die Probleme, die sich aus der Endogenität ergeben.
Höhepunkte
-
Quantile Instrumental-Variablen (IV)-Schätzer
-
Inverse Quantilsregression (IQR)
-
Geglättete Schätzungsgleichungen
-
-
IQR-Schätzer
-
Robuste Konfidenzintervalle für schwache Instrumente
-
Grafische Konvergenzdiagnostik
-
-
Simultane Schätzung über Quantile
-
Visualisierung von Effekten über Quantile
-
Spezialisierte Tests
-
IV hat keinen Einfluss auf das Ergebnis
-
Gleichheit der endogenen Effekte über die Quantile hinweg
-
Effekte größer als Null über alle Quantile hinweg
-
IV ist exogen und nicht endogen
-
Übersicht
Bei der linearen Regression modellieren wir den Mittelwert des Ergebnisses. Manchmal möchten wir jedoch auch andere Merkmale der Ergebnisverteilung als den Mittelwert untersuchen. Zum Beispiel könnte ein Entscheidungsträger erfahren wollen, wie sich die Teilnahme an einem 401(k)-Pensionsplan auf die unteren, mittleren und oberen bedingten Quantile des Nettovermögens auswirkt.
ivqregress schätzt Parameter auf den Quantilen der Ergebnisverteilung und berücksichtigt Endogenitätsprobleme, die aus Gründen wie Selbstselektion, Auslassung einer relevanten Variable oder Messfehler entstehen. Beispielsweise kann die Teilnahme am 401(k)-Programm endogen sein, weil die Personen, die daran teilnehmen und die, die nicht teilnehmen, unterschiedliche Sparpräferenzen haben können, was sich auf das Wachstum des Nettovermögens auswirkt.
Wenn Quantilsregression wichtig ist
Angenommen, wir haben ein einfaches Modell E
E(y|x)=β0+xβ1E
(y|x)=β0+xβ1
, wobei y
die Ergebnisvariable ist und x
x
eine Kovariate ist. x
nimmt
Werte in {0,1,2,3,4,5,6}
. Per Definition, β1β
1
charakterisiert die Auswirkungen der Erhöhung einer Einheit von x
auf den bedingten Mittelwert des Ergebnisses y
; das heißt,
β1=E(y|x=a+1)−E(y|x=a)
β1=E(y|x=a+1)−E(y|x=a)
. Im Folgenden werden wir
zwei Szenarien für den Datenerzeugungsprozess betrachtet.
1. Nur Standortverschiebung. Die Wahrscheinlichkeitsdichtefunktion des Ergebnisses unter der Bedingung
von
x=a+1
x=a+1
f(y|x=a+1)
f(y|x=a+1)
ist nur relativ zu f(y|x=a) ortsverschoben
zu f(y|x=a)
. In diesem Fall, β1
fasst die Wirkung von x
nicht nur für den bedingten Mittelwert, sondern auch für jedes bedingte Quantil
von y
. Dieser Fall ist im linken Feld von Abbildung 1 dargestellt.
2. Standort verschoben und neu skaliert. Die Wahrscheinlichkeitsdichtefunktion des Ergebnisses in Abhängigkeit von
x=a+1
x=a+1
,
f(y|x=a+1)
f(y|x=a+1)
sowohl ortsverschoben als auch neu skaliert relativ zu
f(y|x=a)
f(y|x=a)
.
In diesem Fall,
β1
β1
fasst die Wirkung von x
nur auf den bedingten
Mittelwert, nicht aber auf die bedingten Quantile von y
. Dieser Fall ist dargestellt in
Abbildung 1, rechtes Feld.
Im linken Feld sehen wir, dass jede bedingte Dichte parallel zu den anderen ist; nur der Ort wurde verschoben. In diesem Fall,
β1
erfasst die Verschiebung sowohl des bedingten Mittelwerts als auch aller anderen bedingten Quantile des Ergebnisses. Die Durchführung einer linearen Regression liefert folglich ebenso viele Informationen über
β1
β1
als eine Quantilsregression.
Im Gegensatz dazu wird im rechten Feld die bedingte Dichte für jedes Niveau von x
hat einen anderen Standort und eine andere Form. Daher,
β1
können die Verschiebungen der bedingten Mittelwerte zusammengefasst werden, die sich im Allgemeinen von den Verschiebungen der bedingten Quantile unterscheiden. Die Quantilsregression wird notwendig, um etwas über die Auswirkungen von x
auf die bedingten Quantile des Ergebnisses.
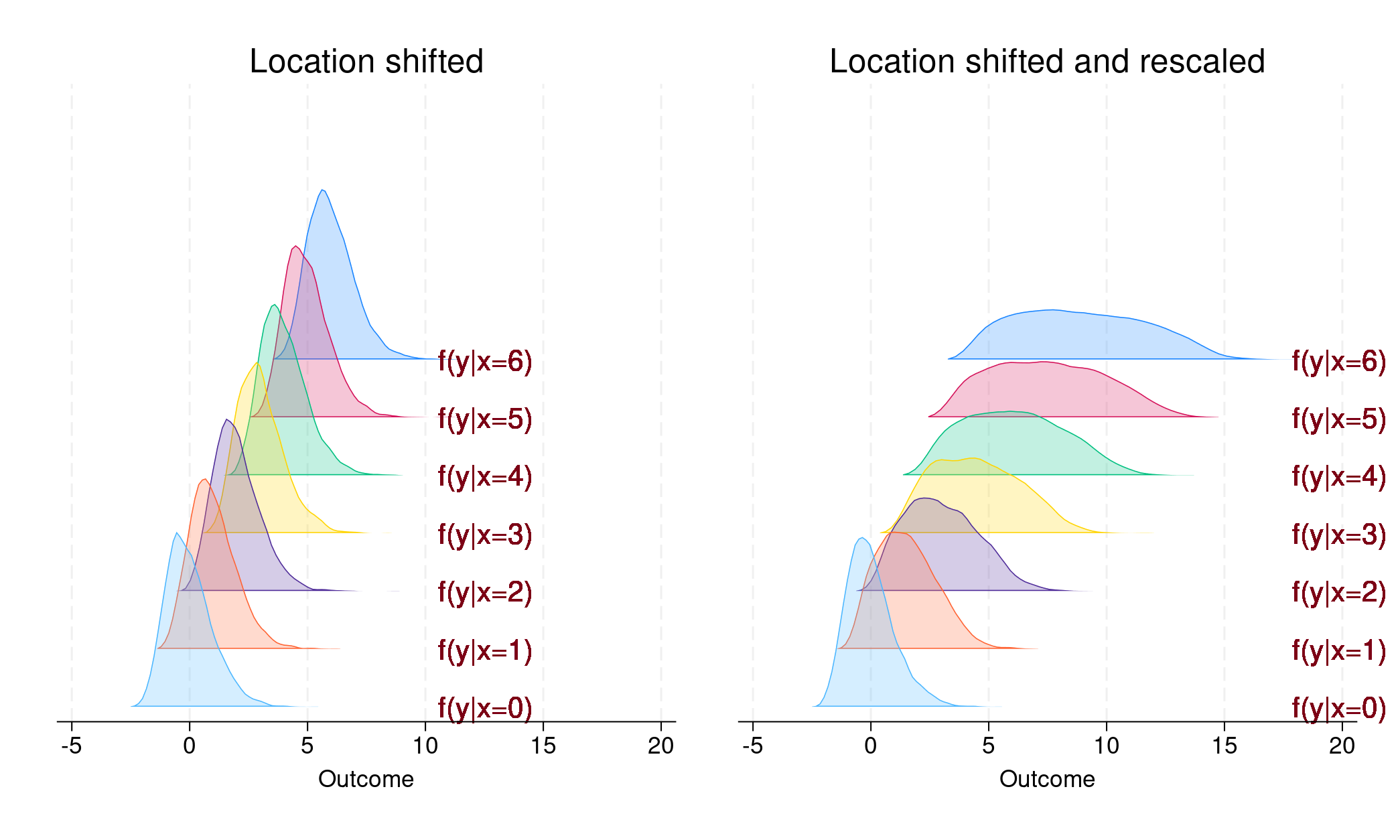
Im linken Feld ist zu sehen, dass jede bedingte Dichte im Verhältnis zu den anderen parallel ist; nur der Ort wurde verschoben. In diesem Fall, β1
�1
erfasst die Verschiebung sowohl des bedingten Mittelwerts als auch aller anderen bedingten Quantile des Ergebnisses. Folglich liefert die Durchführung einer linearen Regression ebenso viele Informationen über β1
�1
als eine Quantilsregression.
Im Gegensatz dazu wird im rechten Feld die bedingte Dichte für jedes Niveau von x
�
hat einen anderen Ort und eine andere Form. Daher ist β1
�1
können die Verschiebungen der bedingten Mittelwerte zusammengefasst werden, die sich im Allgemeinen von den Verschiebungen der bedingten Quantile unterscheiden. Die Quantilsregression wird notwendig, um etwas über die Auswirkungen von x
�
auf die bedingten Quantile des Ergebnisses.
Wir wollen sehen, wie es funktioniert
Wir wollen die Auswirkung der 401(k)-Teilnahme (p401k) auf verschiedene bedingte Quantile des Nettofinanzvermögens (Vermögen) schätzen. Wir verwenden Daten von Chernozhukov und Hansen (2004). Diese Daten stammen aus einer Stichprobe von Haushalten aus dem Survey of Income and Program Participation (SIPP) von 1990. Für den Haushaltsvorstand liegen uns Daten über Einkommen (income), Alter (age), Anzahl der Personen in der Familie (familysize), Familienstand (married), Beteiligung an IRA (ira), Beteiligung an Rentenleistungen (pension), Wohneigentum (ownhome) und Bildungsjahre (educ) vor.
Wir vermuten, dass die Teilnahme an 401(k) endogen ist, da sie von unbeobachteten Faktoren wie der Sparpräferenz abhängen kann, die sich ebenfalls auf das Finanzvermögen auswirken. Wir werden die 401(k)-Anwartschaft (e401k) als Instrument für die 401(k)-Teilnahme verwenden.
Wir verwenden den IQR-Schätzer (ivqregress iqr), um den Effekt der 401(k)-Teilnahme auf den bedingten Median (den Standardwert) des Nettofinanzvermögens zu schätzen.
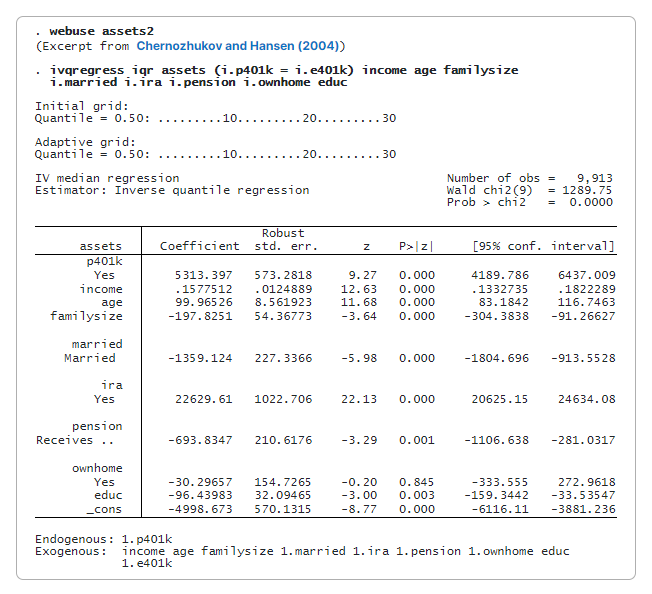
Der Koeffizient für p401k beträgt 5,313. Das bedeutet, dass die Teilnahme an einer 401(k)-Vorsorge das mediane Nettofinanzvermögen um 5.313 $ erhöhen würde, abhängig von anderen Kovariaten, im Vergleich zu einem Szenario, in dem niemand teilnimmt.
Nach ivqregress iqr können wir estat dualci verwenden, um das duale Konfidenzintervall (CI) zu erhalten, das robust gegenüber schwachen Instrumenten für den Koeffizienten der endogenen Variablen ist.
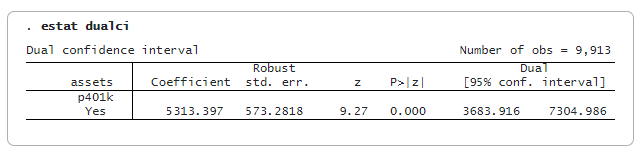
Der duale KI ist in der Regel breiter als der reguläre KI; er bietet robustere Schlussfolgerungen, wenn die Instrumente schwach sind. In diesem Fall ist der duale 95%-KI [3684, 7305], der breiter ist als der reguläre 95%-KI [4190, 6437].
Wir haben den Behandlungseffekt der 401(k)-Beteiligung (p401k) auf den bedingten Median des Nettofinanzvermögens (Vermögen) geschätzt. Aus der Sicht des Politikgestalters könnte es jedoch interessanter sein, den Behandlungseffekt von p401k auf andere bedingte Quantile des Vermögens zu schätzen.
Dieses Mal geben wir ivqregress smooth an, um den Schätzer für geglättete Schätzgleichungen zur Anpassung des Modells an verschiedene Quantile zu verwenden. Insbesondere geben wir die Option quantile(10(10)90) an, um das IVQR-Modell für das 10. und 90. Quantil anzupassen.
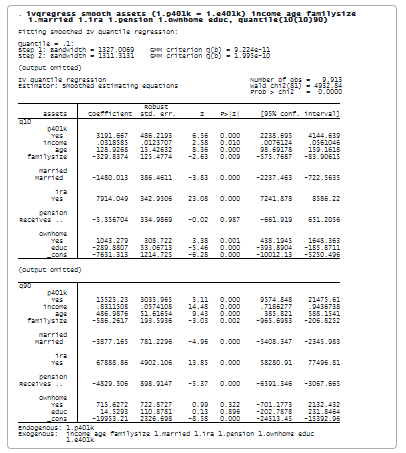
Die Ergebnisse zeigen die Schätzungen für den Effekt der 401(k)-Teilnahme auf jedes bedingte Quantil des Vermögenswerts. Die Interpretation der Koeffizienten ist ähnlich wie zuvor, außer dass wir verschiedene bedingte Quantile betrachten. Für das Quantil q90 beträgt der Schätzwert des Koeffizienten für p401k beispielsweise 15,525. Somit würde die Teilnahme an 401(k) das 90%ige bedingte Quantil des Nettofinanzvermögens um 15.525 $ erhöhen.
Zusätzlich zur Betrachtung der genauen numerischen Schätzungen aus der Koeffiziententabelle können wir estat coefplot verwenden, um den Behandlungseffekt von p401k vom unteren zum oberen Quantil zu visualisieren.
. estat coefplot
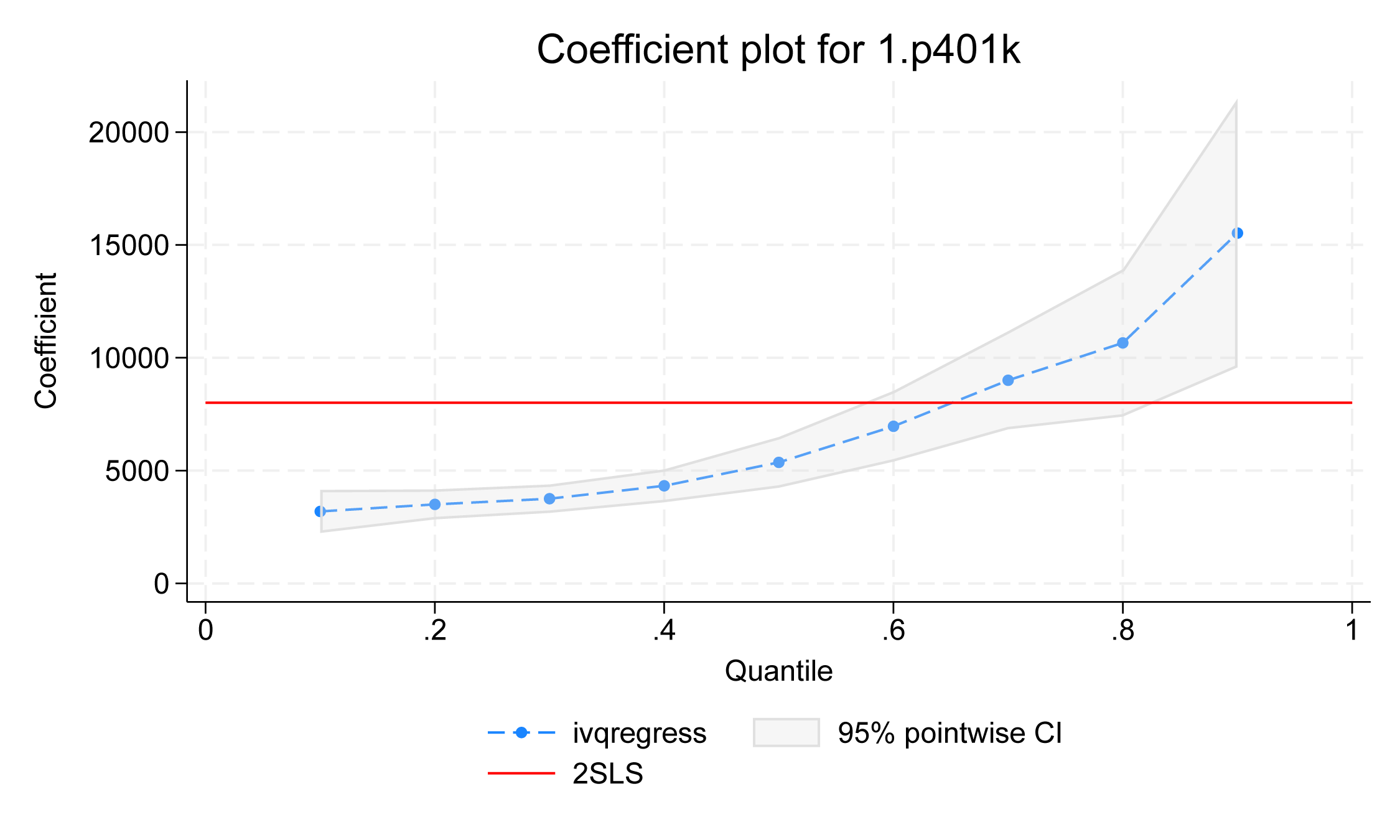
Figure 2
Die Punkte in der Grafik zeigen die Punktschätzungen des Behandlungseffekts von p401k für verschiedene bedingte Quantile des Vermögens, und die graue Grenze zeigt den 95%igen punktweisen KI. Wir sehen einen Aufwärtstrend des Behandlungseffekts von p401k. Bei den unteren Quantilen, wie dem 10., 20., 30. und 40. Der Behandlungseffekt nimmt jedoch in den oberen Quantilen zu. Die rote Linie zeigt die zweistufigen Least-Squares-Schätzungen, die als Benchmark verwendet werden können.
Mit den Estat-Endoeffekten können wir die folgenden Hypothesen bezüglich der endogenen Kovariate testen:
-
Kein Effekt: Die Teilnahme an 401(k) hat für alle geschätzten Quantile keinen Einfluss auf das Nettofinanzvermögen.
-
Konstanter Effekt: Der Behandlungseffekt der 401(k)-Beteiligung ist für alle geschätzten Quantile konstant.
-
Dominanz: Die 401(k)-Beteiligung ist für alle geschätzten Quantile eindeutig positiv, d. h. die Koeffizientenwerte sind streng positiv.
-
Exogenität: Die 401(k)-Beteiligung ist exogen.
Wir verwenden estat endogeffects, um die Kolmogorov-Smirnov-Statistik und den kritischen Wert von 95% für jede Hypothese anzuzeigen. Die Nullhypothese kann verworfen werden, wenn die Teststatistik größer als der kritische Wert ist; andernfalls kann die Nullhypothese nicht verworfen werden. Wir geben die Option rseed() an, um die Ergebnisse reproduzierbar zu machen, da die kritischen Werte aus einer Bootstrap-Stichprobe erzeugt werden.
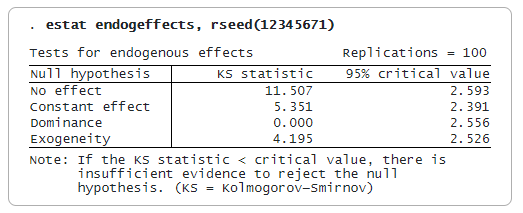
Wir stellen fest, dass die Teilnahme an 401(k) einen gewissen Effekt hat, dass die Behandlung über verschiedene Quantile hinweg nicht konstant ist und dass die Teilnahme an 401(k) endogen ist. Der Dominanztest zeigt, dass die Teilnahme an 401(k) für alle geschätzten Vermögensquantile eindeutig von Vorteil ist.
Die Testergebnisse stimmen mit dem Koeffizientenplot von estat coefplot überein, der zeigt, dass die Behandlungseffekte positiv sind (Hypothese der Dominanz und keine Wirkung) und einen Aufwärtstrend aufweisen (Hypothese der konstanten Wirkung).
Referenz
Chernozhukov, V., und C. Hansen. 2004. The effects of 401(k) participation on the wealth distribution: Eine instrumentelle Quantilsregressionsanalyse. Review of Economics and Statistics 86: 735-751.

