IV квантильна регресія

New In

Квантильна регресія з інструментальними змінними

Коли ми хочемо вивчити вплив коваріатів на різні квантилі результату, ми використовуємо квантильну регресію. Але що робити, якщо ми підозрюємо, що коваріат є ендогенним? Нова команда ivqregress моделює квантилі результату і водночас контролює проблеми, які виникають через ендогенність.

-> Огляд -> Коли квантильна регресія має значення -> Подивимося, як це працює -> Посилання

Основні моменти

Кількісні оцінки інструментальних змінних (IV)
- Обернена квантильна регресія (IQR)
- Згладжені рівняння оцінювання
Оцінювач IQR
- Довірчі інтервали стійкі до слабких інструментів
- Діагностика графічної збіжності
Одночасне оцінювання за квантилями
Візуалізація ефектів за квантилями
Спеціалізовані тести
- IV не впливає на результат
- Рівність ендогенних ефектів у всіх квантилях
- Ефекти більші за нуль у всіх квантилях
- IV є екзогенним, а не ендогенним

Огляд

Коли ми використовуємо лінійну регресію, ми моделюємо середнє значення результату. Але іноді ми хочемо вивчити особливості розподілу результатів, відмінні від середнього значення. Наприклад, політик може захотіти дізнатися, як участь у пенсійному плані 401(k) вплине на нижній, середній та верхній умовні квантилі чистого багатства.

ivqregress оцінює параметри на рівні квантилів розподілу результатів і враховує проблеми ендогенності, які виникають з таких причин, як самостійний відбір, пропуск відповідної змінної або помилка вимірювання. Наприклад, участь у програмі 401(k) може бути ендогенною, оскільки люди, які беруть і не беруть участь у програмі, можуть мати різні уподобання щодо заощаджень, що вплине на зростання чистого багатства.

Коли квантильна регресія має значення

Припустимо, що у нас є проста модель
E(y|x)=
E

(y|x)=β0+xβ1

$// <![CDATA[ E(y|x) = \beta_0 + x\beta_1 // ]]>$

де
y
y
$y$

$// <![CDATA[ y // ]]>$

є змінною результату, а

$x$ $x$

$// <![CDATA[ x // ]]>$

є коваріацією.
x
x $x$

$// <![CDATA[ x // ]]>$

приймає
значення в

${0, 1, 2, 3, 4, 5, 6}$

0,1,2,3,4,5,6}

$// <![CDATA[ \{0, 1, 2, 3, 4, 5, 6\} // ]]>$

. За визначенням,
$β_{1}$

$// <![CDATA[ \beta_1 // ]]>$

повністю характеризує ефект від збільшення на одиницю
x
x
$x$

$// <![CDATA[ x // ]]>$

на умовне середнє значення результату
y
y
$y$

$// <![CDATA[ y // ]]>$

тобто,
$β_{1} = E (y | x = a + 1) - E (y | x = a)$

β1=E(y|x=a+1)−E(y|x=a)

$// <![CDATA[ \beta_1 = E(y|x=a + 1) - E(y|x=a) // ]]>$

. Нижче ми
розглянемо два сценарії процесу генерації даних.

1. Лише зміщення місцезнаходження. Щільність розподілу ймовірностей результату залежить
від

x=a+1

$f (y | x = a + 1)$

f(y|x=a+1)

$// <![CDATA[ f(y|x=a+1) // ]]>$

зміщується лише місце розташування відносно
до
$f (y | x = a)$

f(y|x=a)

$// <![CDATA[ f(y|x=a) // ]]>$

. У цьому випадку,
$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

підсумовує ефект від
x

$// <![CDATA[ x // ]]>$

не тільки на умовному середньому, але й на кожному умовному квантилі
від
y

$// <![CDATA[ y // ]]>$

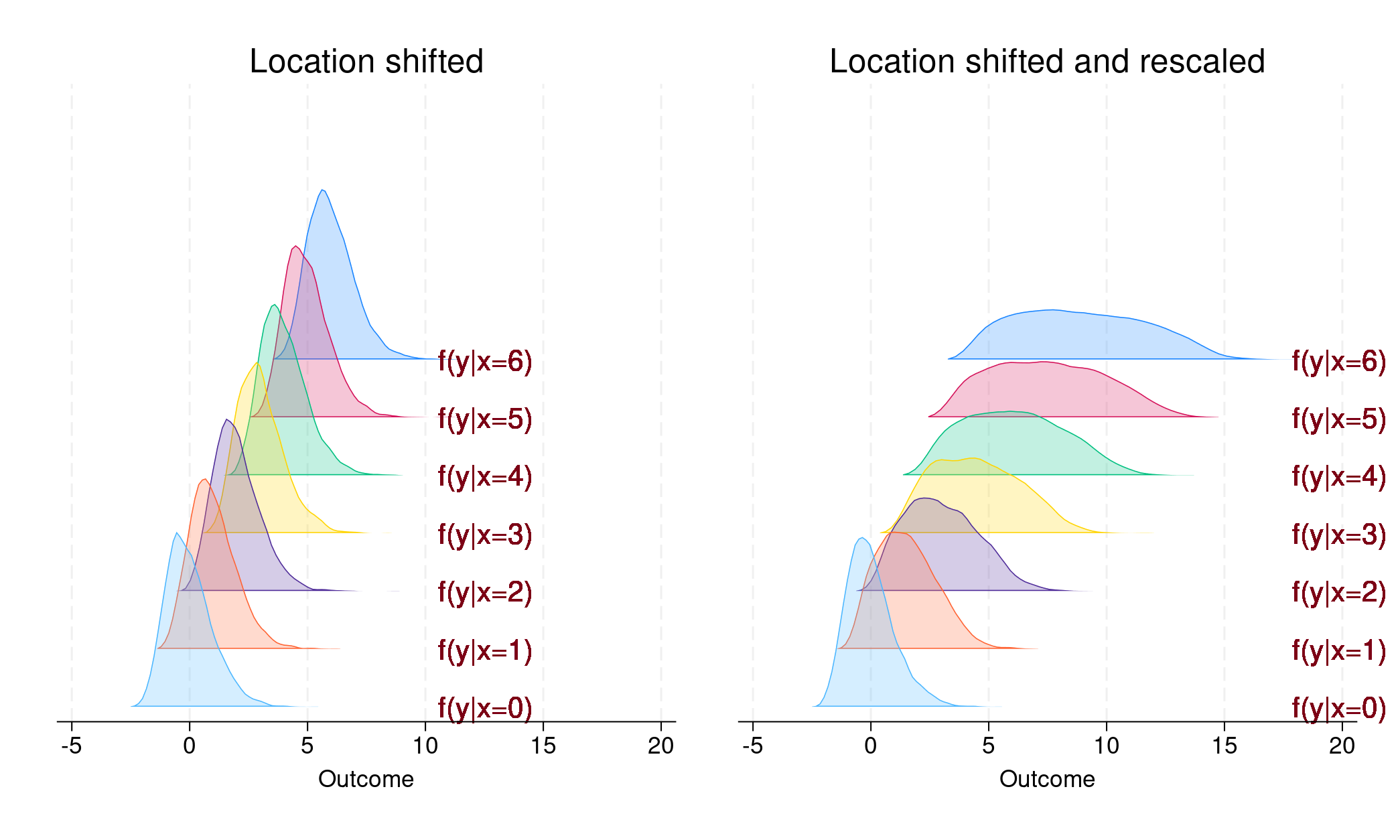
. Цей випадок проілюстровано на лівій панелі Рисунку 1.

2. Розташування зміщено та змінено масштаб. Щільність розподілу ймовірностей результату, що залежить від

x=a+1

$// <![CDATA[ x=a+1 // ]]>$

,
$f (y | x = a + 1)$

f(y|x=a+1)

$// <![CDATA[ f(y|x=a+1) // ]]>$

зміщується і масштабується відносно
$f (y | x = a)$

f(y|x=a)

$// <![CDATA[ f(y|x=a) // ]]>$

.
У цьому випадку,
$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

підсумовує ефект від
$x$

$// <![CDATA[ x // ]]>$

тільки на умовне середнє
середньому, але не на умовних квантилях
y

$// <![CDATA[ y // ]]>$

. Цей випадок проілюстровано на
правій частині Рисунку 1.

Figure 1

На лівій панелі ми бачимо, що кожна умовна щільність паралельна відносно інших; змістилося лише розташування. У цьому випадку
$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

фіксує зсув як умовного середнього, так і будь-яких інших умовних квантилів результату. Як результат, запуск лінійної регресії надає якомога більше інформації про
$β_{1}$

β1

$// <![CDATA[ \beta_1 // ]]>$

як квантильна регресія.

На противагу цьому, на правій панелі умовна щільність для кожного рівня
x

$// <![CDATA[ x // ]]>$

має інше розташування та іншу форму. Таким чином,
β
1

β1

$// <![CDATA[ \beta_1 // ]]>$

може узагальнити зрушення в умовному середньому, які, як правило, відрізняються від зрушень в умовних квантилях. Квантильна регресія стає необхідною, щоб дізнатися про вплив
x

$// <![CDATA[ x // ]]>$

на умовні квантилі результату.

$β_{1}$

як квантильна регресія.

На противагу цьому, на правій панелі умовна щільність для кожного рівня x

$x$

$β_{1}$

$x$

на умовні квантилі результату.

Подивимося, як це працює

Ми хочемо оцінити вплив участі в пенсійній програмі 401(k) (p401k) на різні умовні квантилі чистих фінансових активів (активів). Ми використовуємо дані, наведені в роботі Черножукова та Хансена (2004). Ці дані взяті з вибірки домогосподарств в рамках Обстеження доходів та участі в програмах 1990 року (SIPP). Для голови домогосподарства ми маємо дані про дохід (income), вік (age), кількість осіб у сім’ї (familysize), сімейний стан (married), участь в IRA (ira), участь у пенсійному забезпеченні (pension), власність на житло (ownhome) та роки освіти (educ).

Ми припускаємо, що участь у 401(k) є ендогенною, оскільки вона може залежати від неспостережуваних факторів, таких як перевага заощаджень, які також впливають на фінансові активи. Ми використаємо право на участь у 401(k) (e401k) як інструмент для оцінки участі у 401(k).

Ми використовуємо оцінку IQR (ivqregress iqr), щоб оцінити вплив участі у 401(k) на умовну медіану (дефолт) чистих фінансових активів.

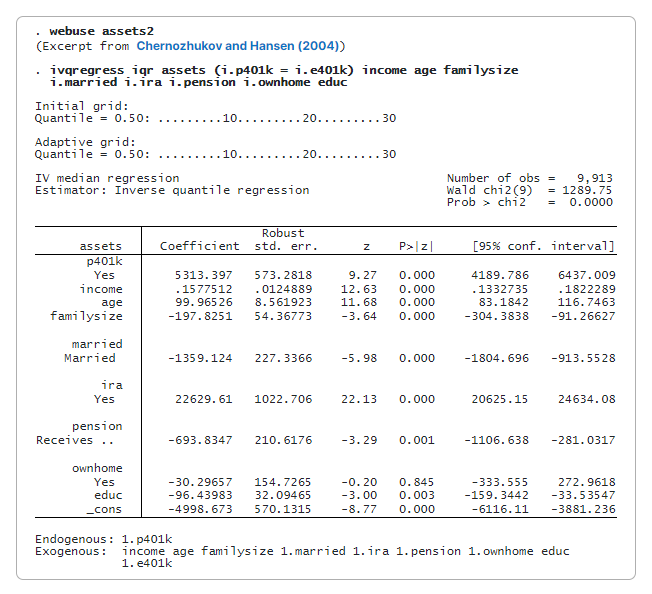
Коефіцієнт для p401k становить 5,313. Це означає, що участь у пенсійному плані 401(k) збільшить медіану чистих фінансових активів на $5,313, за умови інших змінних, порівняно зі сценарієм, де ніхто не бере участі.

Після ivqregress iqr ми можемо використати estat dualci, щоб отримати подвійний довірчий інтервал (ДІ), який є стійким до слабких інструментів для коефіцієнта на ендогенні змінні.

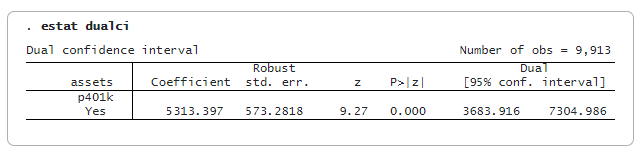
Подвійний ДІ зазвичай ширший, ніж звичайний ДІ; він забезпечує більш надійний висновок, якщо інструменти слабкі. Тут подвійний 95% ДІ становить [3684, 7305], що є ширшим за звичайний 95% ДІ [4190, 6437].

Ми оцінили вплив участі в програмі 401(k) (p401k) на умовну медіану чистих фінансових активів (активів). Однак, з точки зору розробника політики, ми можемо бути більш зацікавлені в оцінці впливу p401k на інші умовні квантилі активів.

Цього разу ми задаємо ivqregress smooth, щоб використовувати згладжені оціночні рівняння для припасування моделі до різних квантилів. Зокрема, ми вказуємо параметр quantile(10(10)90), щоб підігнати модель IVQR до 10-го, 20-го, . . . , 90-му квантилях.

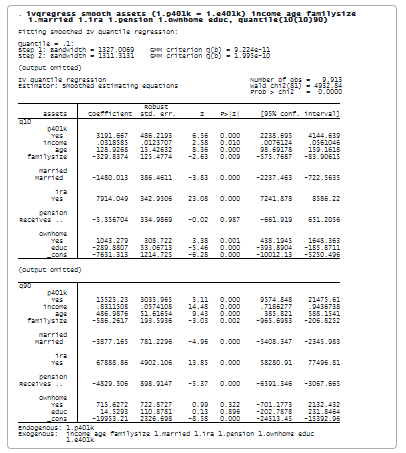
Результати показують оцінки впливу участі в програмі 401(k) на кожен умовний квантиль активу. Інтерпретація коефіцієнта подібна до попередньої, за винятком того, що ми розглядаємо різні умовні квантилі. Наприклад, для квантиля q90 оцінка коефіцієнта на p401k становить 15,525. Таким чином, участь у 401(k) збільшила б 90% умовний квантиль чистих фінансових активів на $15 525.

На додаток до точних числових оцінок з таблиці коефіцієнтів, ми можемо використовувати estat coefplot для візуалізації ефекту лікування за програмою p401k від нижнього до верхнього квантиля.

. estat coefplot

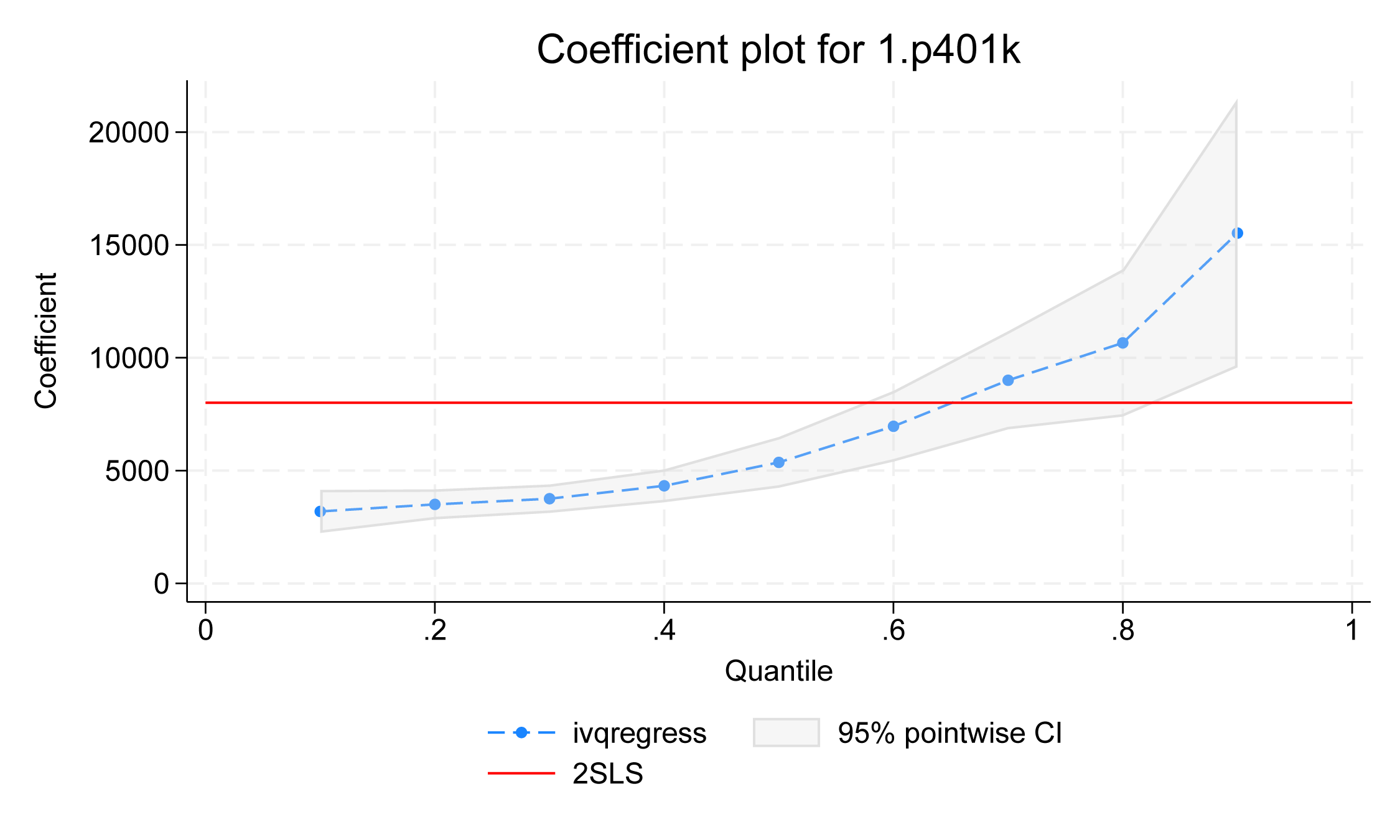
Figure 2

Крапки на графіку показують точкові оцінки впливу p401k на різні умовні квантилі активів, а сіра межа – 95% точковий ДІ. Ми бачимо висхідну тенденцію впливу p401k на лікування. У нижчих квантилях, таких як 10-й, 20-й, 30-й і 40-й квантилі, ефект лікування є відносно рівним. Однак у верхніх квантилях ефект лікування зростає. Червона лінія показує двоступеневі оцінки за методом найменших квадратів, які можна використовувати як орієнтир.

Ми можемо використовувати estat-ендоефекти для перевірки наступних гіпотез щодо ендогенної коваріати:

Відсутність впливу: участь у програмі 401(k) не впливає на чисті фінансові активи для всіх оціночних квантилів.
Постійний вплив: вплив участі в програмі 401(k) є постійним для всіх оціночних квантилів.
Домінування: участь у програмі 401(k) є однозначно позитивною для всіх оціночних квантилів, тобто значення коефіцієнтів є строго позитивними.
Екзогенність: участь 401(k) є екзогенною.

Ми використовуємо estat-ендоефекти, щоб показати статистику Колмогорова-Смірнова та 95% критичне значення для кожної гіпотези. Ми можемо відкинути нульову гіпотезу, якщо тестова статистика більша за критичне значення; в іншому випадку ми не можемо відкинути нульову гіпотезу. Ми вказуємо опцію rseed(), щоб зробити результати відтворюваними, оскільки критичні значення генеруються з бутстреп вибірки.

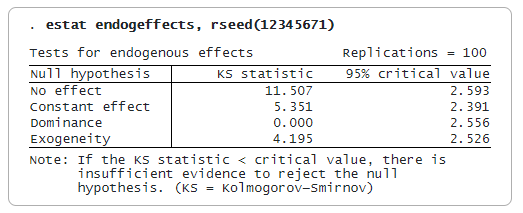
Ми виявили, що участь у 401(k) має певний ефект, ставлення до неї не є постійним для різних квантилів, і що участь у 401(k) є ендогенною. Тест на домінування вказує на те, що участь у 401(k) є однозначно вигідною для всіх оцінених квантилів активів.

Результати тесту узгоджуються з графіком коефіцієнтів, побудованим за допомогою estat coefplot, де ми побачили, що ефекти лікування є позитивними (гіпотези домінування та відсутності ефекту) і мають тенденцію до зростання (гіпотеза постійного ефекту).

Посилання

Черножуков, В. та К. Хансен. 2004. Вплив участі у 401(k) на розподіл багатства: Інструментальний квантильний регресійний аналіз. Огляд економіки та статистики 86: 735-751.

Переглянути всі нові функції

Замовити Stata 18

оновити