New In 
Инструментально-переменная квантильная регрессия
Когда мы хотим изучить влияние ковариаций на различные квантили результата, мы используем квантильную регрессию. Но что делать, если мы подозреваем, что ковариата является эндогенной? Новая команда ivqregress моделирует квантили исхода и одновременно контролирует проблемы, возникающие из-за эндогенности.
Основные моменты
-
Квантильные оценки инструментальных переменных (IV)
-
Обратная квантильная регрессия (IQR)
-
Сглаженные оценочные уравнения
-
-
Оценщик IQR
-
Доверительные интервалы, устойчивые к слабым инструментам
-
Графическая диагностика сходимости
-
-
Одновременное оценивание по квантилям
-
Визуализация эффектов над квантилями
-
Специализированные тесты
-
IV не влияет на результат
-
Равенство эндогенных эффектов по квантилям
-
Эффекты больше нуля для всех квантилей
-
IV является экзогенным, а не эндогенным
-
Обзор
Когда мы используем линейную регрессию, мы моделируем среднее значение результата. Однако иногда мы хотим изучить не только среднее, но и другие характеристики распределения результатов. Например, политик может захотеть узнать, как участие в пенсионном плане 401(k) повлияет на нижний, средний и верхний условные квантили чистого богатства.
ivqregress оценивает параметры по квантилям распределения результатов и учитывает проблемы эндогенности, возникающие по таким причинам, как самоотбор, пропуск соответствующей переменной или ошибка измерения. Например, участие в программе 401(k) может быть эндогенным, поскольку люди, которые участвуют и не участвуют в ней, могут иметь разные предпочтения в отношении сбережений, что повлияет на рост чистого благосостояния.
Когда квантильная регрессия имеет значение
Предположим, у нас есть простая модель
E(y|x)=
E
(y|x)=β0+xβ1
, где
y
y
переменная результата и
x
x
x
является ковариатой.
x
x
принимает
значения в
{0,1,2,3,4,5,6}
{0,1,2,3,4,5,6}{
0,1,2,3,4,5,6}
. По определению,
β1β
1
полностью характеризует эффект от увеличения на одну единицу
x
x
на условное среднее значение исхода
y
y
; то есть,β
1=E(y|x=a+1)−E(y|x=a)
β1=E(y|x=a+1)−E(y|x=a)
. Ниже мы
рассмотрим два сценария процесса генерирования данных.
1. Только смещение местоположения. Функция плотности вероятности исхода при условии
на
x=a+1
x=a+1
f(y|x=a+1)
f(y|x=a+1)
только смещение местоположения относительно
к
f(y|x=a)
f(y|x=a)
. В этом случае,
β1
β1
суммирует эффект от
x
x
не только на условное среднее, но и на каждый условный квантиль
из
y
y
. Этот случай показан на левой панели рис. 1.
2. Смещение и изменение масштаба местоположения. Функция плотности вероятности исхода при условии
x=a+1
x=a+1
,
f(y|x=a+1)
f(y|x=a+1)
, смещается и масштабируется относительно
f(y|x=a)
f(y|x=a)
.
В этом случае,
β
1
β1
суммирует эффект от
x
x
только на условное
среднее, но не на условные квантили
y
y
. Этот случай показан на
правой панели рисунка 1.
На левой панели мы видим, что каждая условная плотность параллельна относительно других, только расположение смещено. В данном случае,
β1
β1
отражает изменение как условного среднего, так и всех остальных условных квантилей результата. В результате линейная регрессия дает столько же информации о
β1
β1
как квантильная регрессия.
Напротив, на правой панели условная плотность для каждого уровня
x
x
имеет другое расположение и другую форму. Таким образом,
β1
β1
может суммировать сдвиги условных средних, которые, как правило, отличаются от сдвигов условных квантилей. Квантильная регрессия становится необходимой для изучения эффектов
x
x
на условные квантили результатов.
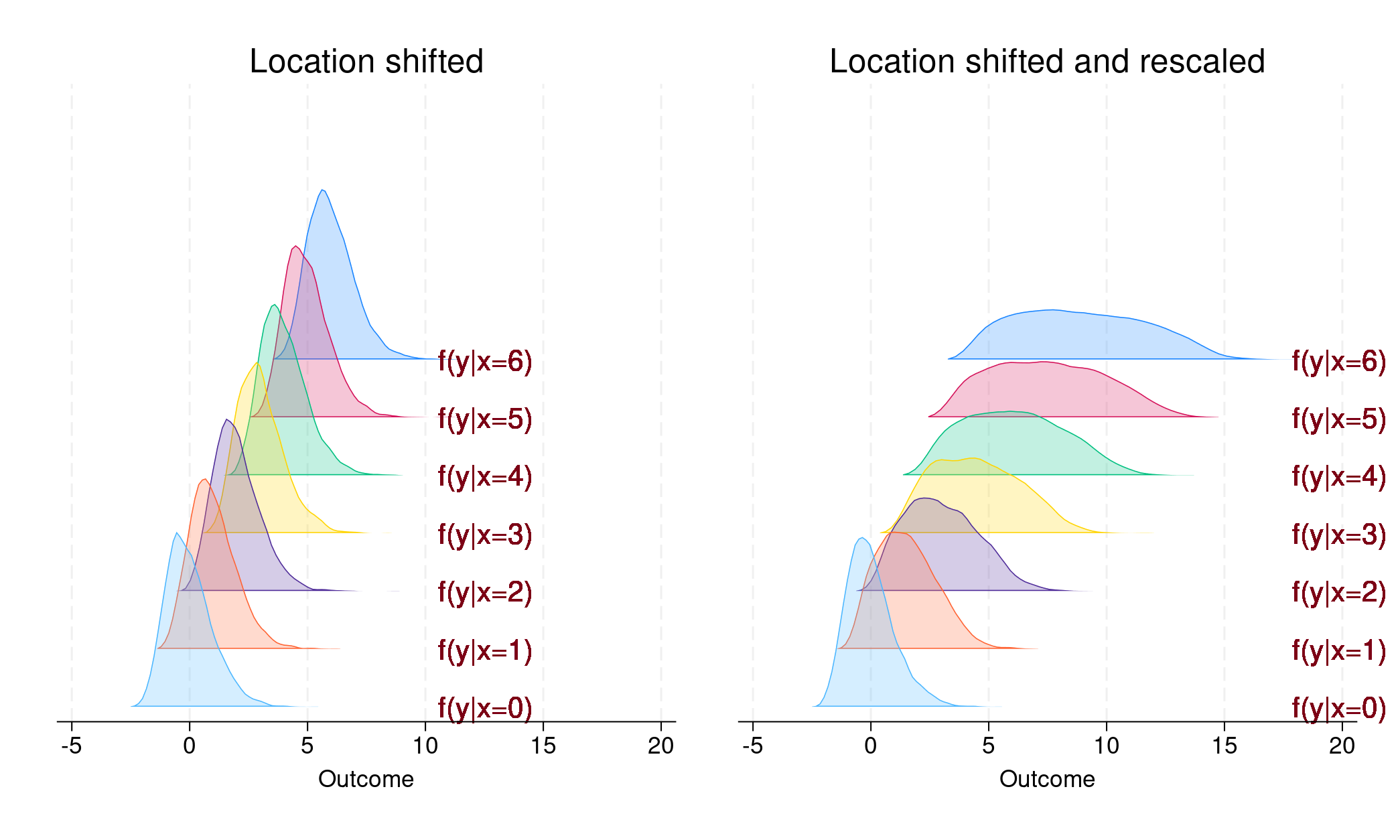
На левой панели мы видим, что каждая условная плотность параллельна остальным, только расположение смещено. В данном случае β1
�1
отражает изменение как условного среднего, так и всех остальных условных квантилей результата. В результате линейная регрессия дает столько же информации о β1
�1
как квантильная регрессия.
Напротив, на правой панели условная плотность для каждого уровня x
�
имеет другое расположение и другую форму. Таким образом, β1
�1
может суммировать сдвиги условных средних, которые, как правило, отличаются от сдвигов условных квантилей. Квантильная регрессия становится необходимой для изучения влияния x
�
на условные квантили результатов.
Давайте посмотрим, как это работает
Мы хотим оценить влияние участия в программе 401(k) (p401k) на различные условные квантили чистых финансовых активов (активов). Мы используем данные, представленные Черножуковым и Хансеном (2004). Эти данные получены на основе выборки домохозяйств из Обзора доходов и участия в программах (SIPP) 1990 года. Для главы домохозяйства у нас есть данные о доходе (income), возрасте (age), количестве человек в семье (familysize), семейном положении (married), участии в IRA (ira), участии в пенсионном обеспечении (pension), владении домом (ownhome) и годах образования (educ).
Мы подозреваем, что участие в программе 401(k) является эндогенным, поскольку оно может зависеть от ненаблюдаемых факторов, таких как предпочтение сбережений, которые также влияют на финансовые активы. Мы используем право на участие в программе 401(k) (e401k) в качестве инструмента для участия в программе 401(k).
Мы используем IQR-оценку (ivqregress iqr) для оценки влияния участия в программе 401(k) на условную медиану (по умолчанию) чистых финансовых активов.
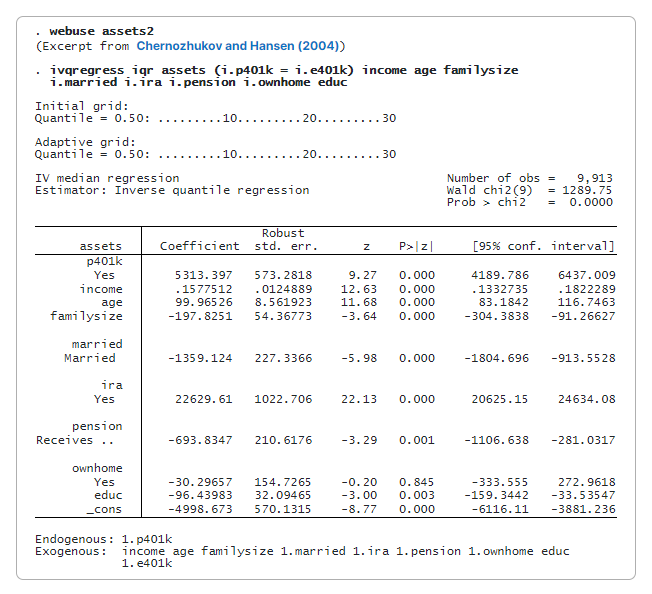
Коэффициент для p401k равен 5,313. Это означает, что участие в программе 401(k) увеличит медианные чистые финансовые активы на 5 313 долларов при условии наличия других ковариаций по сравнению со сценарием, в котором никто не участвует.
После ivqregress iqr мы можем использовать estat dualci, чтобы получить двойной доверительный интервал (CI), устойчивый к слабым инструментам для коэффициентов при эндогенных переменных.
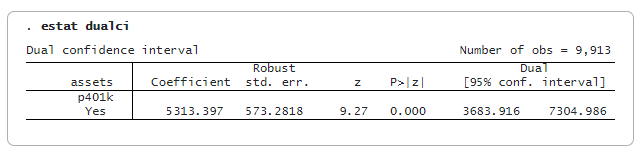
Двойной КИ обычно шире обычного; он обеспечивает более надежные выводы, если инструменты слабы. В данном случае двойной 95%-ный ДИ составляет [3684, 7305], что шире обычного 95%-ного ДИ [4190, 6437].
Мы оценили эффект лечения участия в программе 401(k) (p401k) по условной медиане чистых финансовых активов (активов). Однако с точки зрения разработчика политики нам может быть интереснее оценить эффект лечения p401k для других условных квантилей активов.
На этот раз мы указываем ivqregress smooth, чтобы использовать сглаженную оценку оценочных уравнений для подгонки модели по различным квантилям. В частности, мы указываем опцию quantile(10(10)90), чтобы подогнать модель IVQR по 10-му, 20-му, … , 90-й квантилях.
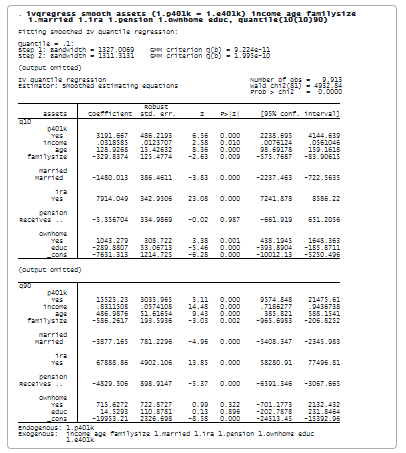
Результаты показывают оценки влияния участия в программе 401(k) на каждый условный квантиль актива. Интерпретация коэффициентов аналогична предыдущей, за исключением того, что мы рассматриваем различные условные квантили. Например, для квантиля q90 оценка коэффициента на p401k составляет 15,525. Таким образом, участие в программе 401(k) увеличит чистые финансовые активы в условном квантиле 90% на 15 525 долларов.
Помимо просмотра точных числовых оценок из таблицы коэффициентов, мы можем использовать estat coefplot для визуализации эффекта лечения p401k от нижнего к верхнему квантилю.
. estat coefplot
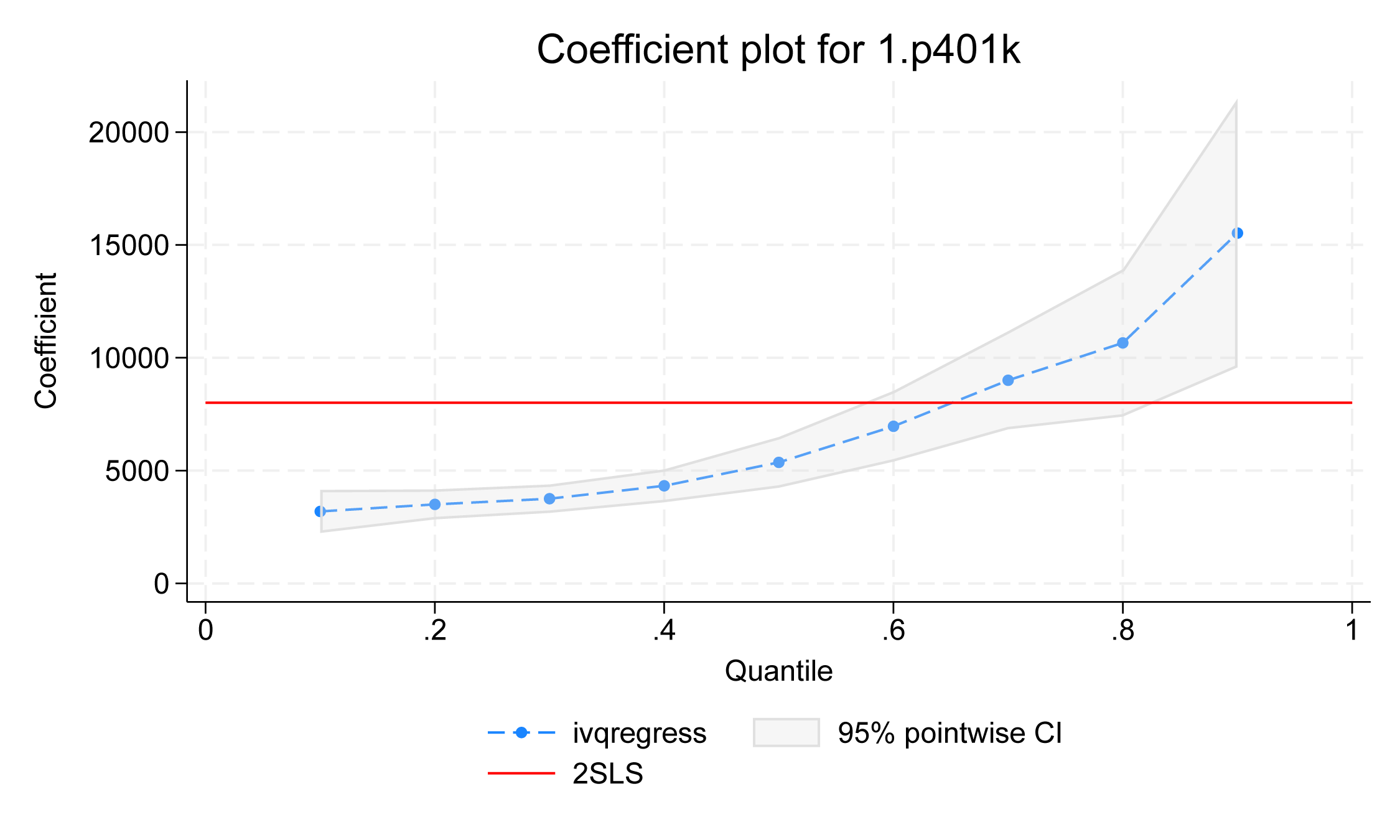
Figure 2
Точки на графике показывают точечные оценки эффекта лечения p401k для различных условных квантилей активов, а серая граница — 95%-ный точечный КИ. Мы видим тенденцию к росту эффекта лечения p401k. На более низких квантилях, таких как 10-й, 20-й, 30-й и 40-й квантили, эффект лечения относительно ровный. Однако эффект лечения увеличивается в квантилях верхнего уровня. Красная линия показывает двухэтапные оценки по методу наименьших квадратов, которые можно использовать в качестве эталона.
Мы можем использовать estat endogeffects для проверки следующих гипотез относительно эндогенной ковариаты:
-
Нет эффекта: участие в программе 401(k) не влияет на чистые финансовые активы для всех расчетных квантилей.
-
Постоянный эффект: эффект лечения от участия впрограмме 401(k) является постоянным для всех расчетных квантилей.
-
Доминирование: участие в программе 401(k) однозначно положительно для всех оцениваемых квантилей; то есть значения коэффициентов строго положительны.
-
Экзогенность: участие в программе 401(k) является экзогенным.
Мы используем estat endogeffects, чтобы показать статистику Колмогорова-Смирнова и 95-процентное критическое значение для каждой гипотезы. Мы можем отвергнуть нулевую гипотезу, если тестовая статистика больше критического значения; в противном случае мы не можем отвергнуть нулевую гипотезу. Мы указываем опцию rseed(), чтобы сделать результаты воспроизводимыми, поскольку критические значения генерируются на основе бутстреп-выборки.
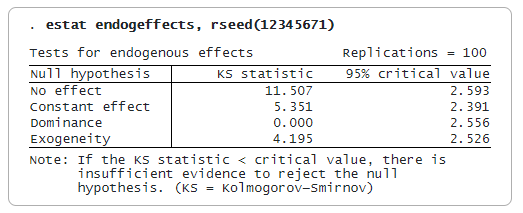
Мы обнаружили, что участие в программе 401(k) имеет определенный эффект, что лечение не является постоянным для разных квантилей и что участие в программе 401(k) является эндогенным. Тест на доминирование показывает, что участие в программе 401(k) однозначно благоприятно для всех оцениваемых квантилей активов.
Результаты теста согласуются с графиком коэффициентов, полученным с помощью estat coefplot, где мы видим, что эффекты лечения положительны (гипотезы доминирования и отсутствия эффекта) и имеют тенденцию к росту (гипотеза постоянного эффекта).
Ссылка
Черножуков, В., и К. Хансен. 2004. Влияние участия в программе 401(k) на распределение богатства: Инструментальный квантильный регрессионный анализ. Обзор экономики и статистики 86: 735-751.

