Often, we do not want to make functional form assumptions about the data we analyze. We may want to fit a regression of an outcome on a set of regressors and be agnostic about the functional form of the regressors. Spline basis functions are flexible approximations to the functional form of the regressors. We may also want to visualize the relationship between an outcome and a regressor or between variables. We may use splines to visualize this relationship without claiming linearity or other functional forms.
In Stata 18, you can use the new makespline command to generate B-spline, piecewise polynomial spline, and restricted cubic spline basis functions from a list of existing variables. For example, we could type
. makespline bspline x1 x2 x3 x4 ...x100
to form 100 third-order B-spline basis functions, one for each variable from x1 to x100. We can now use any of the basis functions to fit a model and be agnostic about the relationship of the covariates and an outcome of interest. Or we could visualize the relationship of the outcome of interest and any of the basis function components that makespline generated.
Let’s see it work
We would like to see the effect of mothers smoking (mbsmoke) on an infant’s birthweight (bweight) using the telasso command. The telasso command lets us model both the outcome (bweight) and the treatment (mbsmoke). We believe that there is a relationship between birthweight and the mother’s age (mage), mother’s educational attainment (medu), and father’s educational attainment (fedu). We also believe that medu is a good predictor of whether a mother smokes during pregnancy.
We are agnostic about the functional form for the relationship of bweight and mage, medu, and fedu. We are also agnostic about the relationship between mbsmoke and medu. This does not matter to telasso. The command selects from a set of candidate covariates and estimates the treatment effect of interest.
We use makespline to form basis functions from each of the covariates of interest.
. makespline bspline mage medu fedu
We generated third-order B-spline basis functions, each consisting of five variables, from mage, medu, and fedu. The variables generated have generic system names, starting with _bsp. If you prefer, you can change the basis names using the basis() option. Below, we show the generated variables:
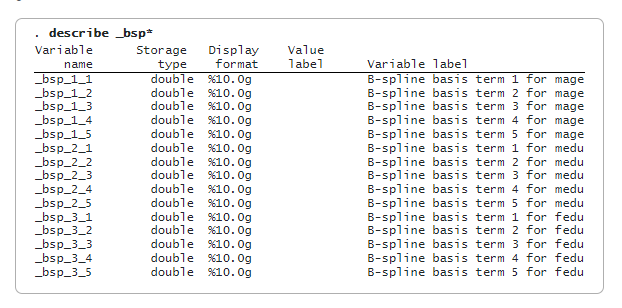
The B-spline basis function components from mage start with_bsp_1, from medu with _bsp_2, and from fedu with _bsp_3. Using these basis functions, we fit the treatment-effects model:
. telasso (bweight c._bsp_1*##c._bsp_2* _bsp_3*) (mbsmoke _bsp_2*)
bweight is an arbitrary function of the interaction (specified by using ##) of the basis functions for mage and medu and of the basis function for father’s education. mbsmoke is an arbitrary function of the basis function for mother’s education. Below are the results:

The basis function variables created by makespline and their interactions produced 40 potential control variables. telasso selected 5 of those controls and used them to compute a treatment effect of –263 grams. In other words, the birthweight of babies would be 263 grams less if all mothers smoked relative to the counterfactual in which no mother smoked.

