Новое в 
Байесовский анализ IRF и FEVD
Impulse–response functions (IRFs), dynamic-multiplier functions, and forecast-error variance decompositions (FEVDs) are commonly used to describe the results from multivariate time-series models such as VAR and DSGE models. These models may have many parameters, which may be difficult to interpret. IRFs and other functions combine the effect of multiple parameters into one summary (per time period). Например, IRF измеряют влияние шока (изменения) одной переменной, такой как уровень инфляции, на определенную итоговую переменную, такую как уровень безработицы.
В Stata 17 вы можете выполнять байесовский анализ IRF с помощью новой команды bayesirf.
Байесовские IRF (и другие функции) вычисляются на основе «точного» апостериорного распределения IRF, которое не зависит от предположения об асимптотической нормальности. Они также могут обеспечить более стабильные оценки для небольших наборов данных, поскольку включают предварительную информацию о параметрах модели.
Вы можете получить IRF и другие функции после подгонки байесовской модели VAR с помощью bayes: var. А байесовские IRF можно получить после подгонки байесовских линейных и нелинейных моделей DSGE с помощью bayes: dsge и bayes: dsgenl.
bayesirf предоставляет несколько подкоманд для создания, построения графиков и таблиц IRF и связанных с ней функций. Вы можете создать несколько результатов IRF и объединить их в таблицах и на графиках. Вы даже можете включить результаты IRF из классического частотного анализа для сравнения.
Основные моменты
- Импульсно-ответные функции
- Динамические множители
- Разложения дисперсии ошибки прогнозирования
- Строить графики и табуляции функций, а также сохранять их в текущих данных
- Укажите горизонт прогнозирования
- Последующие средние или медианы функций
- Постериорные стандартные отклонения
- Последующие доверительные интервалы
- Создание и объединение нескольких результатов IRF
Давайте посмотрим, как это работает
В Байесовских VAR-моделях мы показали базовый Байесовский IRF-анализ, используя макроданные по США, которые представляют собой квартальные данные с первого квартала 1954 года по четвертый квартал 2010 года. Здесь мы покажем больше примеров Байесовского IRF и FEVD анализа.
Мы хотим изучить взаимосвязь между инфляцией, разрывом выпуска и ставкой по федеральным фондам. В частности, нас интересует влияние ставки по федеральным фондам на другие результаты в модели.
Вот данные.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

Мы подогнали байесовскую VAR-модель с тремя лагами. Здесь мы не приводим результаты, но вы можете прочитать больше о команде в разделе Bayesian VAR model.
. quietly bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds, lags(1/3)
Новая команда bayesirf предоставляет несколько подкоманд для Байесовского анализа IRF и FEVD. Три основные из них — bayesirf create, bayesirf graph и bayesirf table. bayesirf create вычисляет IRF и другие функции и сохраняет их в наборе данных IRF, bayesirf graph строит графики, а bayesirf table отображает их в таблице. Другие подкоманды позволяют объединять графики и таблицы нескольких функций и управлять результатами IRF; см. [BAYES] bayesirf.
В классическом анализе IRF (и другие функции) — это одна функция для заданных переменных отклика и импульса. В байесовском анализе мы получаем всю MCMC-выборку IRF, смоделированных из апостериорного распределения. Эта выборка суммируется для получения единой статистики, такой как заднее среднее IRF или заднее среднее IRF.
Мы начинаем с создания IRF и других функций. Мы называем наши результаты IRF как birf и сохраняем их в наборе данных Stata birfex.irf.
. bayesirf create birf, set(birfex) (file birfex.irf created) (file birfex.irf now active) (file birfex.irf updated)
Далее мы построим график IRF с fedfunds в качестве импульсной переменной.
. bayesirf graph irf, impulse(fedfunds)
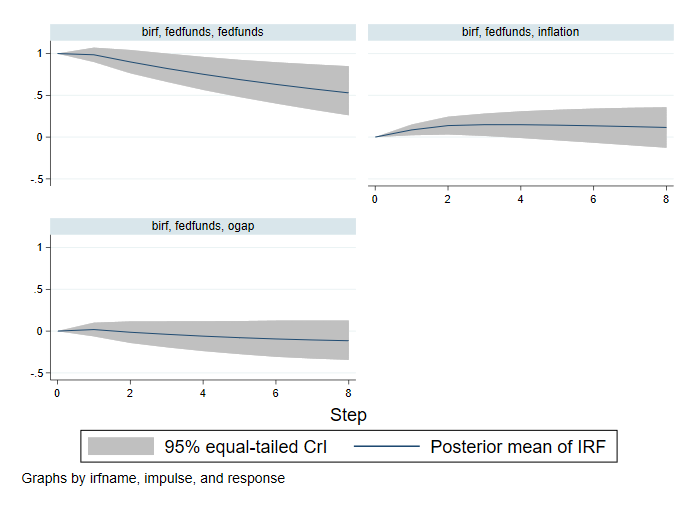
Шоковое воздействие на ставку по федеральным фондам оказывает положительный эффект на саму себя, который уменьшается со временем, но остается положительным через восемь кварталов. Шок ставки по федеральным фондам оказывает незначительное влияние на разрыв выпуска и небольшой положительный эффект на инфляцию, который исчезает через два квартала.
Мы можем увидеть результаты в таблице.
. bayesirf table irf, response(ogap) impulse(fedfunds) Results from birf
| (1) (1) (1) | ||
| Step | irf Lower Upper | |
| 0 | 0 0 0 | |
| 1 | .018505 -.062511 .10086 | |
| 2 | -.013814 -.141146 .116743 | |
| 3 | -.038081 -.193427 .117507 | |
| 4 | -.060205 -.238349 .118354 | |
| 5 | -.078581 -.275435 .120713 | |
| 6 | -.093737 -.307345 .126362 | |
| 7 | -.105821 -.328061 .126226 | |
| 8 | -.115108 -.344162 .127231 | |
Мы можем увидеть влияние шока на более длительном горизонте, указав большее количество временных периодов в опции step() программы bayesirf create. Мы заменяем текущие результаты и дополнительно сохраняем выборку IRF MCMC в birfsim.dta. (Нам нужны результаты IRF MCMC, если мы хотим вычислить доверительные интервалы, отличные от 95% равнохвостых интервалов по умолчанию, с помощью подкоманд bayesirf, что мы продемонстрируем позже).
. bayesirf create birf, set(birfex) step(25) mcmcsaving(birfsim) replace (file birfex.irf now active) file birfsim.dta saved. (file birfex.irf updated) . bayesirf graph irf, impulse(fedfunds)
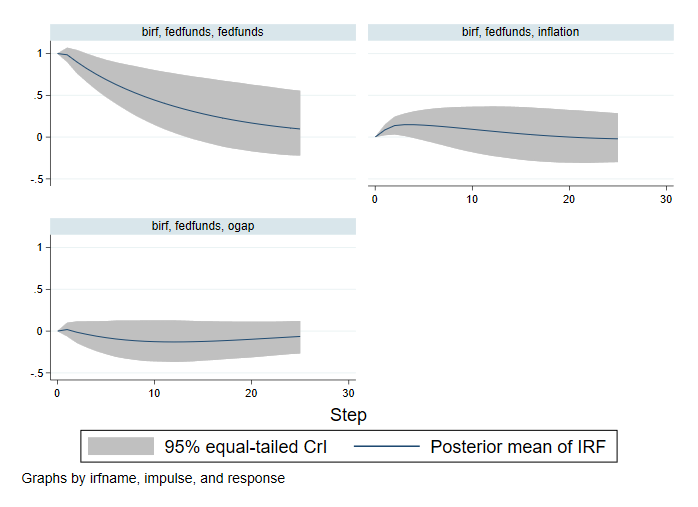
Добавление большего количества временных периодов позволяет нам глубже изучить динамику ставки по федеральным фондам. Шок на ставку по федеральным фондам оказывает положительное влияние на саму себя в течение первых 14 кварталов. Мы не смогли наблюдать этот эффект в предыдущем примере с более коротким горизонтом. Наши выводы о влиянии ставки по федеральным фондам на другие переменные остаются прежними.
Мы можем посмотреть на другие функции и построить их рядом, используя bayesirf cgraph. Давайте построим график ортогональных IRF и FEVD.
. bayesirf cgraph (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd)
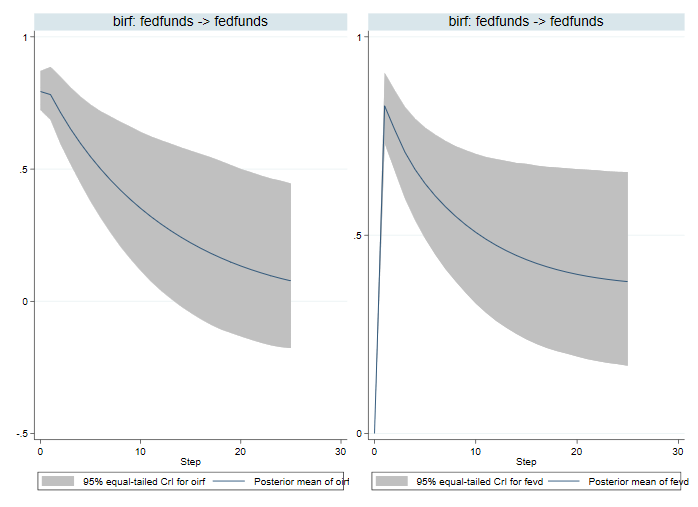
Ортогональные ИРФ (ОИРФ) описывают импульсный отклик на шок, равный одному стандартному отклонению. FEVD измеряет долю дисперсии ошибки, которая объясняется шоком для ставки по федеральным фондам. Показатели OIRF подтверждают наши предыдущие выводы, основанные на IRF. FEVD показывает, что шок от fedfunds преобладает на первом этапе, но затем уменьшается с течением времени.
Мы также можем отобразить несколько результатов в таблице, используя bayesirf ctable. Для краткости мы показываем только первые три шага.
. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3)
| (1) (1) (1) | ||
| Step | oirf Lower Upper | |
| 0 | .793208 .72369 .870942 | |
| 1 | .781637 .686623 .886267 | |
| 2 | .713651 .594886 .848175 | |
| 3 | .652003 .518588 .808557 | |
| (1) (1) (1) | ||
| Step | fevd Lower Upper | |
| 0 | 0 0 0 | |
| 1 | .825878 .731612 .909342 | |
| 2 | .765772 .661851 .86463 | |
| 3 | .709687 .593096 .823202 | |
Вместо стандартных апостериорных средних и доверительных интервалов с равными хвостами мы можем сообщить апостериорные медианы и доверительные интервалы HPD. (Мы можем это сделать, потому что мы уже сохранили результаты IRF MCMC с помощью bayesirf create ранее).
. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3) median hpd
| (1) (1) (1) | ||
| Step | oirf Lower Upper | |
| 0 | .79167 .720032 .86681 | |
| 1 | .780219 .686243 .884995 | |
| 2 | .7111 .590842 .842952 | |
| 3 | .648349 .512718 .799466 | |
| (1) (1) (1) | ||
| Step | fevd Lower Upper | |
| 0 | 0 0 0 | |
| 1 | .827376 .737115 .913222 | |
| 2 | .766713 .664094 .865899 | |
| 3 | .710221 .593963 .823788 | |
Вы также можете использовать опцию clevel(), чтобы изменить 95% уровень достоверности по умолчанию.
После анализа мы удаляем файлы, созданные bayes: var и bayesirf create, если они нам больше не нужны.
. erase bvarsim.dta . erase birfsim.dta . erase birfex.irf
