Să vedem cum funcționează

În modelele Bayesiene VAR, am arătat analiza Bayesian IRF de bază folosind macrodatele din SUA, care sunt date trimestriale din primul trimestru al anului 1954 până în al patrulea trimestru al 2010. Aici vom arăta mai multe exemple de analize Bayesian IRF și FEVD.
Vrem să studiem relațiile dintre inflație, decalajul de producție și rata fondurilor federale. În special, suntem interesați de efectul ratei fondurilor federale asupra celorlalte rezultate ale modelului.
Iată datele.

. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)

. tsset

Time variable: date, 1954q3 to 2010q4
        Delta: 1 quarter

. tsline inflation ogap fedfunds

Ne potrivim unui model Bayesian VAR cu trei decalaje. Suprimăm ieșirea din acesta aici, dar puteți citi mai multe despre comandă în modelul Bayesian VAR.

. quietly bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds, lags(1/3)

Noua comandă bayesirf oferă mai multe subcomenzi pentru analiza Bayesian IRF și FEVD. Cele trei principale sunt bayesirf create, bayesirf graph și bayesirf table. bayesirf creează calcule IRF și alte funcții și le salvează într-un set de date IRF, graficul bayesirf le reprezintă, iar tabelul bayesirf le afișează într-un tabel. Alte subcomenzi vă permit să combinați grafice și tabele cu mai multe funcții și să vă gestionați rezultatele IRF; vezi [BAYES] bayesirf.
În analiza clasică, un IRF (și alte funcții) este o funcție unică pentru răspunsul dat și variabilele de impuls. În analiza bayesiană, obținem un întreg eșantion MCMC de IRF simulat din distribuția posterioară. Acest eșantion este rezumat pentru a produce o singură statistică, cum ar fi IRF mediu posterior sau IRF median posterior.
Începem cu crearea IRF-urilor și a altor funcții. Denumim rezultatele noastre IRF ca birf și le salvăm într-un set de date Stata birfex.irf.

. bayesirf create birf, set(birfex)
(file birfex.irf created)
(file birfex.irf now active)
(file birfex.irf updated)

Apoi, trasăm IRF cu fedfunds ca variabilă de impuls.

. bayesirf graph irf, impulse(fedfunds)

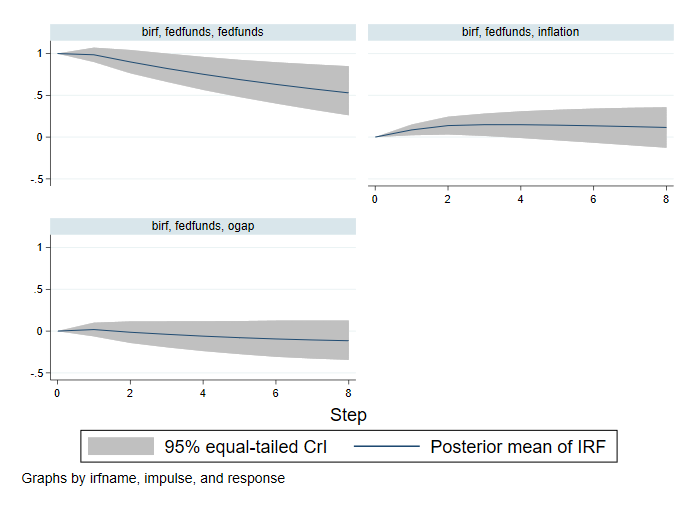
Un șoc asupra ratei fondurilor federale are un efect pozitiv asupra sa, care scade în timp, dar este încă pozitiv după opt trimestre. Șocul ratei fondurilor federale are un efect redus asupra decalajului de producție și un mic efect pozitiv asupra inflației care dispare după două trimestre.
Putem vedea rezultatele într-un tabel.

. bayesirf table irf, response(ogap) impulse(fedfunds)

Results from birf



         
 
      (1)         (1)         (1)  
    Step 
 
      irf       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .018505    -.062511      .10086
       2 
 
 -.013814    -.141146     .116743
       3 
 
 -.038081    -.193427     .117507
       4 
 
 -.060205    -.238349     .118354
       5 
 
 -.078581    -.275435     .120713
       6 
 
 -.093737    -.307345     .126362
       7 
 
 -.105821    -.328061     .126226
       8 
 
 -.115108    -.344162     .127231

Posterior means reported.
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = ogap.

Putem vedea efectele unui șoc pe un orizont mai lung prin specificarea mai multor perioade de timp în opțiunea step() a bayesirf create. Înlocuim rezultatele actuale și salvăm suplimentar eșantionul IRF MCMC în birfsim.dta. (Avem nevoie de rezultate IRF MCMC dacă dorim să calculăm intervale credibile, altele decât intervalele implicite de 95% cu coadă egală cu subcomandele bayesirf, pe care le demonstrăm mai târziu.)

. bayesirf create birf, set(birfex) step(25) mcmcsaving(birfsim) replace
(file birfex.irf now active)
file birfsim.dta saved.
(file birfex.irf updated)

. bayesirf graph irf, impulse(fedfunds)

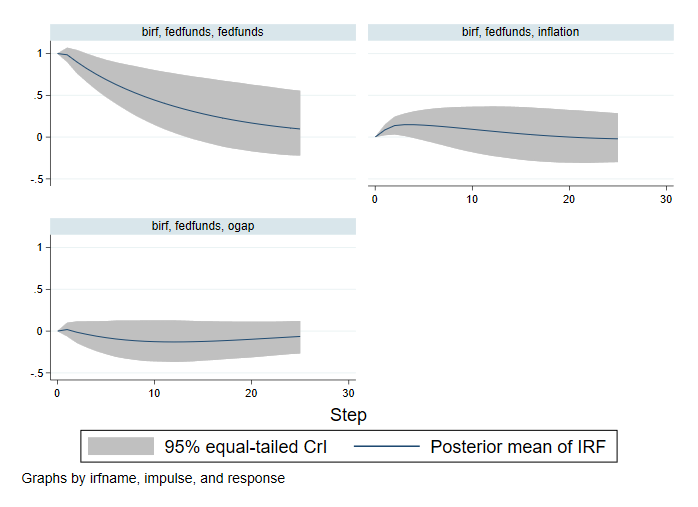
Adăugarea mai multor perioade de timp ne permite să explorăm în continuare dinamica ratei fondurilor federale. Un șoc asupra ratei fondurilor federale are un efect pozitiv asupra sa în primele 14 trimestre. Nu am putut observa acest efect în exemplul anterior cu orizontul mai scurt. Concluziile noastre despre efectul ratei fondurilor federale asupra altor variabile rămân aceleași.
Ne putem uita la alte funcții și le putem parcela una lângă alta folosind bayesirf cgraph. Să trasăm IRF ortogonal și FEVD.

. bayesirf cgraph (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd)

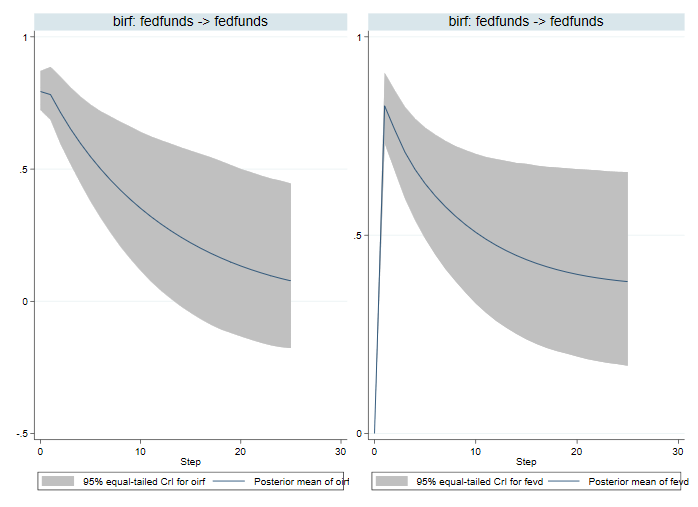
IRF ortogonale (OIRF) descriu răspunsul impulsului la un șoc cu deviație standard. FEVD măsoară fracțiunea varianței erorii care se explică printr-un șoc la rata fondurilor federale. OIRF susține concluziile noastre anterioare bazate pe IRF. FEVD arată că șocul asupra fondurilor alimentare este predominant în primul pas, dar apoi scade în timp.
De asemenea, putem afișa mai multe rezultate într-un tabel utilizând bayesirf ctable. Pentru scurtă durată, arătăm doar primii trei pași.

. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3)



         
 
      (1)         (1)         (1)  
    Step 
 
     oirf       Lower       Upper  

       0 
 
  .793208      .72369     .870942
       1 
 
  .781637     .686623     .886267
       2 
 
  .713651     .594886     .848175
       3 
 
  .652003     .518588     .808557





         
 
      (1)         (1)         (1)  
    Step 
 
     fevd       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .825878     .731612     .909342
       2 
 
  .765772     .661851      .86463
       3 
 
  .709687     .593096     .823202

Posterior means reported.
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = fedfunds.

În locul mijloacelor posterioare implicite și a intervalelor credibile cu coadă egală, putem raporta mediane posterioare și intervale credibile HPD. (Putem face acest lucru deoarece am salvat deja rezultatele IRF MCMC mai devreme cu bayesirf create).

. bayesirf ctable (birf fedfunds fedfunds oirf) (birf fedfunds fedfunds fevd), step(3) median hpd



         
 
      (1)         (1)         (1)  
    Step 
 
     oirf       Lower       Upper  

       0 
 
   .79167     .720032      .86681
       1 
 
  .780219     .686243     .884995
       2 
 
    .7111     .590842     .842952
       3 
 
  .648349     .512718     .799466





         
 
      (1)         (1)         (1)  
    Step 
 
     fevd       Lower       Upper  

       0 
 
        0           0           0
       1 
 
  .827376     .737115     .913222
       2 
 
  .766713     .664094     .865899
       3 
 
  .710221     .593963     .823788

Posterior medians reported.
95% HPD credible lower and upper bounds reported.
(1) irfname = birf, impulse = fedfunds, and response = fedfunds.

De asemenea, puteți utiliza opțiunea clevel() pentru a schimba nivelul implicit de credibilitate de 95%.
După analiză, eliminăm fișierele create de bayes: var și bayesirf create dacă nu mai avem nevoie de ele.

. erase bvarsim.dta
. erase birfsim.dta
. erase birfex.irf