New In 
Zero-inflated ordered logit model
Stata’s new ziologit command fits zero-inflated ordered logit models.
Ordered logit regression is used to model ordered categorical responses, such as symptom severity recorded as none, mild, moderate, or severe. Larger values of such ordered outcomes represent higher levels, but the numeric value is irrelevant.
In some situations, more zeros (or more values in the lowest category) are observed in the data than would be expected by a traditional ordered logit model. A zero might represent the absence of a trait while the remaining values represent increasing levels of the trait. Many zeros may be observed, some because the individual does not have the trait, and some because an individual has the trait but exhibits the lowest level. For example,
In a study of alcohol consumption, some individuals report no consumption because they never drink alcohol while others may report no alcohol consumption because they did not drink in the survey period.
In a clinical trial of a treatment intended to shrink tumors, outcomes represent no improvement, partial response, or complete response. An individual may show no improvement because the tumor is resistant to treatment or because the tumor was treatable but did not shrink at the time of measurement. The distinction is important because treatable tumors are good candidates for a higher dose.
In contexts such as these, you can use a zero-inflated ordered logit (ZIOL) model. ZIOL models assume that the lowest-valued outcomes come from both a logit model and an ordered logit model, allowing different sets of predictors for each model.
Highlights
- Model ordinal data with an overabundance of responses in the lowest category
- Use a logit model to identify zero inflation and an ordered logit model for the ordinal response
- Use a potentially different set of predictors for the logit and ordered logit model
- Easily interpret findings using odds ratios and marginal probabilities
- Support for Bayesian estimation
- Robust, cluster–robust, and bootstrap standard errors
- Complex survey designs support
Let’s see it work
For this example, we will use fictional data on cigarette consumption.
. use https://www.stata-press.com/data/r17/tobacco
The outcome of interest, tobacco, represents daily cigarette consumption as an ordinal response with four levels:
. codebook tobacco
| tobacco Tobacco usage | ||||||
| Type: Numeric (byte) | ||||||
| Label: tobaclbl | ||||||
| Range: [0,3] Units: 1 | ||||||
| Unique values: 4 Missing .: 0/15,000 | ||||||
| Tabulation: Freq. Numeric Label | ||||||
| 9,469 0 0 cigarettes | ||||||
| 3,806 1 1–7 cigarettes/day | ||||||
| 1,050 2 8–12 cigarettes/day | ||||||
| 675 3 >12 cigarettes/day | ||||||
More than half of the respondents reported no cigarette consumption. We suspect that these respondents belong to one of two groups: nonsmokers and would-be smokers with no current smoking activity. A traditional ordered logit regression can model the level of cigarette consumption among smokers, but it cannot distinguish between the two groups of respondents who reported no cigarette consumption. The ZIOL model introduces the concept of succeptibility to smoking, wherein smokers (both active and would-be) are susceptible to smoking, while genuine nonsmokers are not susceptible to smoking. To allow for the possibility of genuine nonsmokers, we choose the ZIOL model over the traditional ordered logit model.
We will use ziologit to simultaneously model the level of cigarette consumption and the probability of being a smoker. To model the level of cigarette consumption, we include predictors in the ziologit command directly after the dependent variable tobacco. To model the probability of being a smoker, we include predictors in the inflate() option, so named because it is used to model zero inflation. The inflate() option is required because excluding it would be tantamount to fitting a traditional ordered logit model.
Suppose that we want to regress the level of cigarette consumption on years of education (education), income in $10,000s (income), and gender (female), while we want to model the probability of being a smoker with independent variables education and income, as well as a variable indicating whether either of the respondent’s parents smoked (parent).
We could fit this model using the following command:
. ziologit tobacco education income i.female, inflate(income education i.parent)
Iteration 0: log likelihood = -15977.364 (not concave)
Iteration 1: log likelihood = -13149.83 (not concave)
Iteration 2: log likelihood = -12467.245
Iteration 3: log likelihood = -11039.218
Iteration 4: log likelihood = -9929.2298
Iteration 5: log likelihood = -9715.1143
Iteration 6: log likelihood = -9703.2464
Iteration 7: log likelihood = -9703.2168
Iteration 8: log likelihood = -9703.2168
Zero-inflated ordered logit regression Number of obs = 15,000
Wald chi2(3) = 3147.70
Log likelihood = -9703.2168 Prob > chi2 = 0.0000
| tobacco | Coefficient Std. err. z P>|z| [95% conf. interval] | |||||
| tobacco | ||||||
| education | .5090816 .0094838 53.68 0.000 .4904938 .5276695 | |||||
| income | .583636 .0114401 51.02 0.000 .5612139 .6060581 | |||||
| female | ||||||
| Female | -.5307721 .0580736 -9.14 0.000 -.6445943 -.4169499 | |||||
| inflate | ||||||
| income | -.1279677 .00705 -18.15 0.000 -.1417856 -.1141499 | |||||
| education | -.1412459 .0049693 -28.42 0.000 -.1509855 -.1315062 | |||||
| parent | ||||||
| Smoking | 1.187864 .0529432 22.44 0.000 1.084097 1.29163 | |||||
| _cons | 2.617219 .1156891 22.62 0.000 2.390473 2.843966 | |||||
| /cut1 | 5.85957 .104449 5.654853 6.064286 | |||||
| /cut2 | 11.14187 .1945483 10.76056 11.52318 | |||||
| /cut3 | 14.3632 .2495117 13.87417 14.85224 | |||||
There are three sections to the results table. The first section, labeled tobacco, contains coefficients from the ordered logit model for the level of cigarette consumption. The second section, labeled inflate, contains coefficients from the logit model for the probability of being a smoker. The third section contains the cutpoints from the ordered logit model.
To interpret the first two sections of the results table, the coefficients can be exponentiated and reported as odds ratios with the or option.
. ziologit, or
Zero-inflated ordered logit regression Number of obs = 15,000
Wald chi2(3) = 3147.70
Log likelihood = -9703.2168 Prob > chi2 = 0.0000
| tobacco | Odds ratio Std. err. z P>|z| [95% conf. interval] | |||||
| tobacco | ||||||
| education | 1.663763 .0157788 53.68 0.000 1.633122 1.694978 | |||||
| income | 1.792544 .0205068 51.02 0.000 1.752799 1.833191 | |||||
| female | ||||||
| Female | .5881507 .034156 -9.14 0.000 .5248755 .659054 | |||||
| inflate | ||||||
| income | .8798818 .0062032 -18.15 0.000 .8678073 .8921242 | |||||
| education | .8682758 .0043147 -28.42 0.000 .8598602 .8767738 | |||||
| parent | ||||||
| Smoking | 3.280066 .1736572 22.44 0.000 2.956768 3.638714 | |||||
| _cons | 13.69758 1.584661 22.62 0.000 10.91866 17.18378 | |||||
| /cut1 | 5.85957 .104449 5.654853 6.064286 | |||||
| /cut2 | 11.14187 .1945483 10.76056 11.52318 | |||||
| /cut3 | 14.3632 .2495117 13.87417 14.85224 | |||||
Here we see that a $10,000 increase in annual income decreases the odds of being a smoker by a factor of 0.88 (12% decrease in odds), but, among smokers, increases the odds of higher cigarette consumption by a factor of 1.79 (79% increase in odds). This suggests that wealthier individuals are less likely to smoke, but if they do decide to smoke, they tend to smoke more cigarettes.
But what do these results really mean in terms of the probability of exhibiting different smoking behavior? We can use margins to answer different questions using the parameters of our model. Say we are interested at the relation of cigarette consumption and income level. Below, we estimate the probabilities for each level of cigarette consumption at annual incomes of $0, $50,000, $100,000, $150,000, and $200,000.
. margins, at(income=(0(5)20)) Predictive margins Number of obs = 15,000 Model VCE: OIM 1._predict : Pr(tobacco=0), predict(pmargin outcome(0)) 2._predict : Pr(tobacco=1), predict(pmargin outcome(1)) 3._predict : Pr(tobacco=2), predict(pmargin outcome(2)) 4._predict : Pr(tobacco=3), predict(pmargin outcome(3)) 1._at: income = 0 2._at: income = 5 3._at: income = 10 4._at: income = 15 5._at: income = 20
| Delta-method | ||||||
| Margin std. err. z P>|z| [95% conf. interval] | ||||||
| _predict#_at | ||||||
| 1 1 | .7428698 .0044443 167.15 0.000 .7341591 .7515805 | |||||
| 1 2 | .6190759 .0038733 159.83 0.000 .6114843 .6266675 | |||||
| 1 3 | .5168462 .0052057 99.29 0.000 .5066433 .5270492 | |||||
| 1 4 | .526699 .0092168 57.15 0.000 .5086344 .5447636 | |||||
| 1 5 | .6340465 .0138387 45.82 0.000 .6069232 .6611697 | |||||
| 2 1 | .2121431 .0034296 61.86 0.000 .2054211 .2188651 | |||||
| 2 2 | .2792459 .0033861 82.47 0.000 .2726092 .2858826 | |||||
| 2 3 | .3042245 .0040212 75.65 0.000 .2963431 .312106 | |||||
| 2 4 | .2226386 .0050478 44.11 0.000 .2127452 .232532 | |||||
| 2 5 | .0633686 .0047963 13.21 0.000 .0539681 .0727692 | |||||
| 3 1 | .0372614 .0014098 26.43 0.000 .0344983 .0400245 | |||||
| 3 2 | .0737865 .0019981 36.93 0.000 .0698702 .0777027 | |||||
| 3 3 | .1146585 .0029075 39.44 0.000 .1089599 .1203572 | |||||
| 3 4 | .1351544 .0041403 32.64 0.000 .1270395 .1432693 | |||||
| 3 5 | .138638 .0052133 26.59 0.000 .1284201 .1488559 | |||||
| 4 1 | .0077257 .0005647 13.68 0.000 .0066189 .0088324 | |||||
| 4 2 | .0278917 .0011614 24.01 0.000 .0256153 .030168 | |||||
| 4 3 | .0642707 .002228 28.85 0.000 .0599038 .0686376 | |||||
| 4 4 | .115508 .0045623 25.32 0.000 .1065661 .12445 | |||||
| 4 5 | .1639469 .0085572 19.16 0.000 .147175 .1807188 | |||||
Here we calculate the expected probabilities of each level of cigarette consumption at $0, $50,000, $100,000, $150,000, and $200,000 annual income.
In the output table, there are many combinations of income and cigarrete consumption levels. In such cases, it is more effective to present the results graphically. We can visualize the expected probabilities over all income levels by using marginsplot.
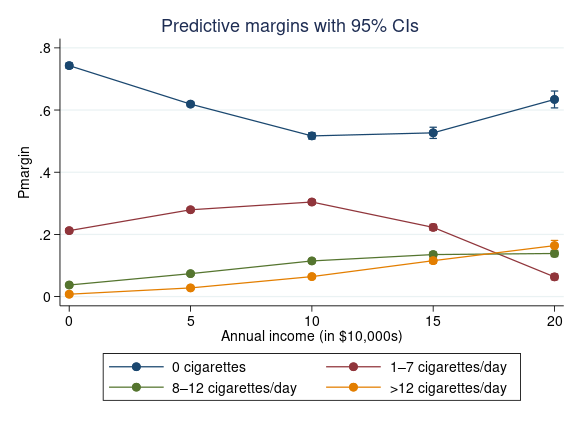
The probability of smoking 0 cigarettes decreases as annual income increases until $100,000, then the probability gradually increases again. The probability of smoking 1–7 cigarettes/day is highest when earnings are $100,000 per year, and lowest when earnings are $200,000 per year.
After reviewing the overall probability of each outcome, we want to examine the relationship between income and the susceptibility to smoking. We use margins to calculate ps, the probability of susceptibility, at the same five levels of income.
. quietly margins, predict(ps) at(income=(0(5)20)) . marginsplot

Four-fifths of respondents when income is zero are either smokers or would-be smokers. The probability of being a smoker decreases with increasing income, with just over a third of respondents susceptible to smoking when earnings are $200,000 per year. This supports the interpretation that income may act as a proxy for health consciousness.
Next we use margins to focus on subjects who are susceptible to smoking. By specifying statistic pcond1 along with each outcome level, we calculate the probability of each level of tobacco, conditional on susceptibility. As before, calculations are performed at five levels of income and graphed with marginsplot.
. quietly margins, predict(pcond1 outcome(0)) predict(pcond1 outcome(1)) predict(pcond1 outcome(2)) predict(pcond1 outcome(3)) at(income=(0(5)20))
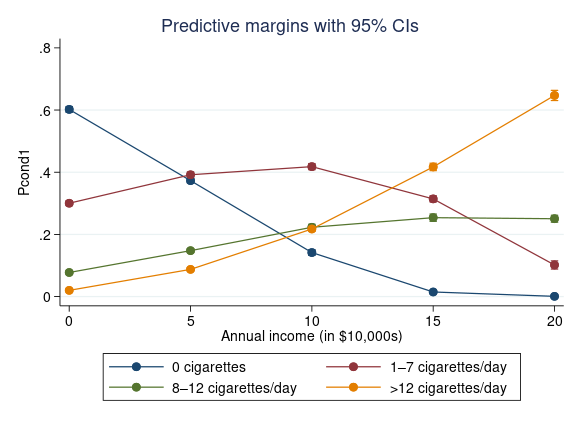
Well over half of the would-be smokers, when annual income is zero, report 0 cigarette consumption, and those that do consume cigarettes are most likely to smoke just a few cigarettes per day. As income increases, the probability of 0 consumption falls, with virtually all smokers expected to have positive cigarette consumption when earnings are $200,000 per year. Higher annual income is associated with a higher probability of being a heavy smoker: the probability of consuming 1–7 cigarettes per day begins to fall as annual income exceeds $100,000, while the probability of consuming >12 cigarettes per day increases with income to become the most common smoking outcome when income is highest. This suggests that, among smokers, cigarettes are treated as what economists call a normal good; that is, something for which demand increases when income increases.
We can see from this example that the effect of income on cigarette consumption is multifaceted. The ziologit command makes it possible to model smoking susceptibility as well as smoking intensity, leading to a better understanding of the factors influencing smoking behavior.
