Nouveau dans 
Modèle logit ordonné à dégonflement nul
La nouvelle commande ziologit de Stata permet d’ajuster les modèles logit ordonnés à dégonflement nul.
La régression logit ordonnée est utilisée pour modéliser des réponses catégorielles ordonnées, telles que la gravité des symptômes enregistrée comme nulle, légère, modérée ou grave. Des valeurs plus élevées de ces résultats ordonnés représentent des niveaux plus élevés, mais la valeur numérique n’est pas pertinente.
Dans certaines situations, on observe plus de zéros (ou plus de valeurs dans la catégorie la plus basse) dans les données que ne le voudrait un modèle logit ordonné traditionnel. Un zéro peut représenter l’absence d’un trait tandis que les autres valeurs représentent des niveaux croissants du trait. De nombreux zéros peuvent être observés, certains parce que l’individu ne possède pas le trait, et d’autres parce qu’un individu possède le trait mais présente le niveau le plus bas. Par exemple,
Dans une étude sur la consommation d’alcool, certains individus ne déclarent aucune consommation parce qu’ils ne boivent jamais d’alcool, tandis que d’autres peuvent déclarer ne pas avoir consommé d’alcool parce qu’ils n’ont pas bu pendant la période d’enquête.
Dans un essai clinique d’un traitement destiné à réduire les tumeurs, les résultats représentent une absence d’amélioration, une réponse partielle ou une réponse complète. Un individu peut ne présenter aucune amélioration parce que la tumeur est résistante au traitement ou parce que la tumeur était traitable mais n’a pas diminué au moment de la mesure. La distinction est importante car les tumeurs traitables sont de bons candidats pour une dose plus élevée.
Dans de tels contextes, vous pouvez utiliser un modèle logit ordonné gonflé à zéro (ZIOL). Les modèles ZIOL supposent que les résultats de plus faible valeur proviennent à la fois d’un modèle logit et d’un modèle logit ordonné, en autorisant différents ensembles de prédicteurs pour chaque modèle.
Points forts
- Modéliser des données ordinales avec une surabondance de réponses dans la catégorie la plus basse
- Utilisez un modèle logit pour identifier l’inflation zéro et un modèle logit ordonné pour la réponse ordinale.
- Utilisez un ensemble de prédicteurs potentiellement différents pour le modèle logit et le modèle logit ordonné.
- Interprétez facilement les résultats à l’aide des rapports de cotes et des probabilités marginales.
- Prise en charge de l’estimation bayésienne
- Erreurs standard robustes, robustes en grappes et bootstrap.
- Prise en charge des plans d’enquête complexes
Voyons comment cela fonctionne
Pour cet exemple, nous utiliserons des données fictives sur la consommation de cigarettes.
. use https://www.stata-press.com/data/r17/tobacco
Le résultat d’intérêt, le tabac, représente la consommation quotidienne de cigarettes sous la forme d’une réponse ordinale à quatre niveaux :
. codebook tobacco
| tobacco Tobacco usage | ||||||
| Type: Numeric (byte) | ||||||
| Label: tobaclbl | ||||||
| Range: [0,3] Units: 1 | ||||||
| Unique values: 4 Missing .: 0/15,000 | ||||||
| Tabulation: Freq. Numeric Label | ||||||
| 9,469 0 0 cigarettes | ||||||
| 3,806 1 1–7 cigarettes/day | ||||||
| 1,050 2 8–12 cigarettes/day | ||||||
| 675 3 >12 cigarettes/day | ||||||
Plus de la moitié des répondants ont déclaré ne pas consommer de cigarettes. Nous pensons que ces personnes appartiennent à l’un des deux groupes suivants : les non-fumeurs et les fumeurs potentiels qui ne fument pas actuellement. Une régression logit ordonnée traditionnelle peut modéliser le niveau de consommation de cigarettes chez les fumeurs, mais elle ne peut pas faire la distinction entre les deux groupes de répondants qui ont déclaré ne pas consommer de cigarettes. Le modèle ZIOL introduit le concept de succeptibilité au tabagisme, selon lequel les fumeurs (actifs et potentiels) sont susceptibles de fumer, tandis que les véritables non-fumeurs ne le sont pas. Pour tenir compte de la possibilité de véritables non-fumeurs, nous avons choisi le modèle ZIOL plutôt que le modèle logit ordonné traditionnel.
Nous allons utiliser ziologit pour modéliser simultanément le niveau de consommation de cigarettes et la probabilité d’être fumeur. Pour modéliser le niveau de consommation de cigarettes, nous incluons des prédicteurs dans la commande ziologit directement après la variable dépendante tabac. Pour modéliser la probabilité d’être fumeur, nous incluons des prédicteurs dans l’option inflate(), ainsi nommée car elle est utilisée pour modéliser l’inflation zéro. L’option inflate() est nécessaire car l’exclure reviendrait à ajuster un modèle logit ordonné traditionnel.
Supposons que nous voulions régresser le niveau de consommation de cigarettes sur le nombre d’années d’études (études), le revenu en milliers de dollars (revenu) et le sexe (femme), tandis que nous voulons modéliser la probabilité d’être fumeur avec les variables indépendantes études et revenu, ainsi qu’une variable indiquant si l’un des parents de la personne interrogée fumait (parent).
Nous pourrions ajuster ce modèle en utilisant la commande suivante:
. ziologit tobacco education income i.female, inflate(income education i.parent)
Iteration 0: log likelihood = -15977.364 (not concave)
Iteration 1: log likelihood = -13149.83 (not concave)
Iteration 2: log likelihood = -12467.245
Iteration 3: log likelihood = -11039.218
Iteration 4: log likelihood = -9929.2298
Iteration 5: log likelihood = -9715.1143
Iteration 6: log likelihood = -9703.2464
Iteration 7: log likelihood = -9703.2168
Iteration 8: log likelihood = -9703.2168
Zero-inflated ordered logit regression Number of obs = 15,000
Wald chi2(3) = 3147.70
Log likelihood = -9703.2168 Prob > chi2 = 0.0000
| tobacco | Coefficient Std. err. z P>|z| [95% conf. interval] | |||||
| tobacco | ||||||
| education | .5090816 .0094838 53.68 0.000 .4904938 .5276695 | |||||
| income | .583636 .0114401 51.02 0.000 .5612139 .6060581 | |||||
| female | ||||||
| Female | -.5307721 .0580736 -9.14 0.000 -.6445943 -.4169499 | |||||
| inflate | ||||||
| income | -.1279677 .00705 -18.15 0.000 -.1417856 -.1141499 | |||||
| education | -.1412459 .0049693 -28.42 0.000 -.1509855 -.1315062 | |||||
| parent | ||||||
| Smoking | 1.187864 .0529432 22.44 0.000 1.084097 1.29163 | |||||
| _cons | 2.617219 .1156891 22.62 0.000 2.390473 2.843966 | |||||
| /cut1 | 5.85957 .104449 5.654853 6.064286 | |||||
| /cut2 | 11.14187 .1945483 10.76056 11.52318 | |||||
| /cut3 | 14.3632 .2495117 13.87417 14.85224 | |||||
Le tableau des résultats comporte trois sections. La première section, intitulée tabac, contient les coefficients du modèle logit ordonné pour le niveau de consommation de cigarettes. La deuxième section, intitulée gonfler, contient les coefficients du modèle logit pour la probabilité d’être fumeur. La troisième section contient les points de coupure du modèle logit ordonné.
Pour interpréter les deux premières sections du tableau de résultats, les coefficients peuvent être exponentiés et présentés sous forme de rapports de cotes avec l’option ou .
. ziologit, or
Zero-inflated ordered logit regression Number of obs = 15,000
Wald chi2(3) = 3147.70
Log likelihood = -9703.2168 Prob > chi2 = 0.0000
| tobacco | Odds ratio Std. err. z P>|z| [95% conf. interval] | |||||
| tobacco | ||||||
| education | 1.663763 .0157788 53.68 0.000 1.633122 1.694978 | |||||
| income | 1.792544 .0205068 51.02 0.000 1.752799 1.833191 | |||||
| female | ||||||
| Female | .5881507 .034156 -9.14 0.000 .5248755 .659054 | |||||
| inflate | ||||||
| income | .8798818 .0062032 -18.15 0.000 .8678073 .8921242 | |||||
| education | .8682758 .0043147 -28.42 0.000 .8598602 .8767738 | |||||
| parent | ||||||
| Smoking | 3.280066 .1736572 22.44 0.000 2.956768 3.638714 | |||||
| _cons | 13.69758 1.584661 22.62 0.000 10.91866 17.18378 | |||||
| /cut1 | 5.85957 .104449 5.654853 6.064286 | |||||
| /cut2 | 11.14187 .1945483 10.76056 11.52318 | |||||
| /cut3 | 14.3632 .2495117 13.87417 14.85224 | |||||
Nous constatons ici qu’une augmentation de 10 000 $ du revenu annuel diminue la probabilité d’être fumeur d’un facteur de 0,88 (diminution de 12 % de la probabilité), mais, parmi les fumeurs, augmente la probabilité d’une plus grande consommation de cigarettes d’un facteur de 1,79 (augmentation de 79 % de la probabilité). Cela suggère que les personnes plus riches sont moins susceptibles de fumer, mais si elles décident de le faire, elles ont tendance à fumer davantage de cigarettes.
Mais que signifient réellement ces résultats en termes de probabilité de présenter un comportement tabagique différent ? Nous pouvons utiliser les marges pour répondre à différentes questions en utilisant les paramètres de notre modèle. Disons que nous nous intéressons à la relation entre la consommation de cigarettes et le niveau de revenu. Ci-dessous, nous estimons les probabilités pour chaque niveau de consommation de cigarettes pour des revenus annuels de 0, 50 000, 100 000, 150 000 et 200 000 dollars.
. margins, at(income=(0(5)20)) Predictive margins Number of obs = 15,000 Model VCE: OIM 1._predict : Pr(tobacco=0), predict(pmargin outcome(0)) 2._predict : Pr(tobacco=1), predict(pmargin outcome(1)) 3._predict : Pr(tobacco=2), predict(pmargin outcome(2)) 4._predict : Pr(tobacco=3), predict(pmargin outcome(3)) 1._at: income = 0 2._at: income = 5 3._at: income = 10 4._at: income = 15 5._at: income = 20
| Delta-method | ||||||
| Margin std. err. z P>|z| [95% conf. interval] | ||||||
| _predict#_at | ||||||
| 1 1 | .7428698 .0044443 167.15 0.000 .7341591 .7515805 | |||||
| 1 2 | .6190759 .0038733 159.83 0.000 .6114843 .6266675 | |||||
| 1 3 | .5168462 .0052057 99.29 0.000 .5066433 .5270492 | |||||
| 1 4 | .526699 .0092168 57.15 0.000 .5086344 .5447636 | |||||
| 1 5 | .6340465 .0138387 45.82 0.000 .6069232 .6611697 | |||||
| 2 1 | .2121431 .0034296 61.86 0.000 .2054211 .2188651 | |||||
| 2 2 | .2792459 .0033861 82.47 0.000 .2726092 .2858826 | |||||
| 2 3 | .3042245 .0040212 75.65 0.000 .2963431 .312106 | |||||
| 2 4 | .2226386 .0050478 44.11 0.000 .2127452 .232532 | |||||
| 2 5 | .0633686 .0047963 13.21 0.000 .0539681 .0727692 | |||||
| 3 1 | .0372614 .0014098 26.43 0.000 .0344983 .0400245 | |||||
| 3 2 | .0737865 .0019981 36.93 0.000 .0698702 .0777027 | |||||
| 3 3 | .1146585 .0029075 39.44 0.000 .1089599 .1203572 | |||||
| 3 4 | .1351544 .0041403 32.64 0.000 .1270395 .1432693 | |||||
| 3 5 | .138638 .0052133 26.59 0.000 .1284201 .1488559 | |||||
| 4 1 | .0077257 .0005647 13.68 0.000 .0066189 .0088324 | |||||
| 4 2 | .0278917 .0011614 24.01 0.000 .0256153 .030168 | |||||
| 4 3 | .0642707 .002228 28.85 0.000 .0599038 .0686376 | |||||
| 4 4 | .115508 .0045623 25.32 0.000 .1065661 .12445 | |||||
| 4 5 | .1639469 .0085572 19.16 0.000 .147175 .1807188 | |||||
Nous calculons ici les probabilités attendues de chaque niveau de consommation de cigarettes à 0, 50 000, 100 000, 150 000 et 200 000 dollars de revenu annuel.
Dans le tableau de sortie, il existe de nombreuses combinaisons de revenus et de niveaux de consommation de cigares. Dans ce cas, il est plus efficace de présenter les résultats sous forme de graphique. Nous pouvons visualiser les probabilités attendues pour tous les niveaux de revenu en utilisant marginsplot.
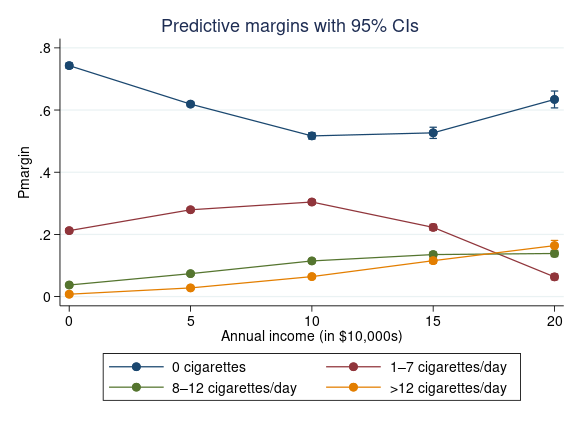
La probabilité de ne pas fumer de cigarettes diminue à mesure que le revenu annuel augmente jusqu’à 100 000 $, puis la probabilité augmente à nouveau progressivement. La probabilité de fumer de 1 à 7 cigarettes par jour est la plus élevée lorsque le revenu annuel est de 100 000 $, et la plus faible lorsque le revenu annuel est de 200 000 $.
Après avoir examiné la probabilité globale de chaque résultat, nous voulons examiner la relation entre le revenu et la susceptibilité au tabagisme. Nous utilisons les marges pour calculer ps, la probabilité de susceptibilité, aux cinq mêmes niveaux de revenu.
. quietly margins, predict(ps) at(income=(0(5)20)) . marginsplot

Les quatre cinquièmes des répondants dont le revenu est nul sont soit des fumeurs, soit des fumeurs potentiels. La probabilité d’être fumeur diminue avec l’augmentation du revenu, avec un peu plus d’un tiers des répondants susceptibles de fumer lorsque le revenu est de 200 000 dollars par an. Cela confirme l’interprétation selon laquelle le revenu peut agir comme un indicateur de la conscience de la santé.
Ensuite, nous utilisons lesmarges pour nous concentrer sur les sujets qui sont susceptibles de fumer. En spécifiant la statistique pcond1 avec chaque niveau de résultat, nous calculons la probabilité de chaque niveau de tabac, conditionnellement à la susceptibilité. Comme précédemment, les calculs sont effectués à cinq niveaux de revenu et représentés graphiquement avec marginsplot.
. quietly margins, predict(pcond1 outcome(0)) predict(pcond1 outcome(1)) predict(pcond1 outcome(2)) predict(pcond1 outcome(3)) at(income=(0(5)20))
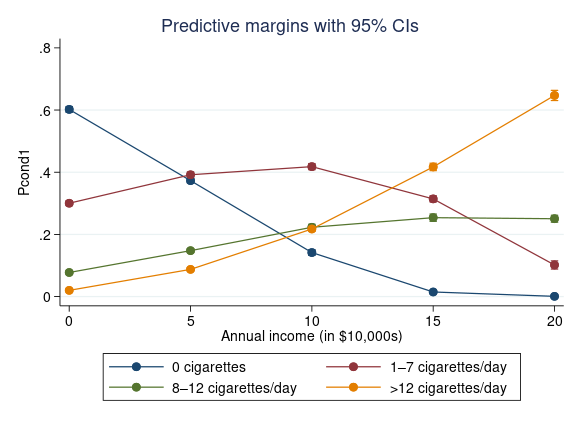
Bien plus de la moitié des fumeurs potentiels, lorsque le revenu annuel est nul, déclarent une consommation nulle de cigarettes, et ceux qui consomment des cigarettes sont plus susceptibles de ne fumer que quelques cigarettes par jour. Au fur et à mesure que le revenu augmente, la probabilité d’une consommation nulle diminue, la quasi-totalité des fumeurs devant avoir une consommation positive de cigarettes lorsque le revenu est de 200 000 dollars par an. Un revenu annuel plus élevé est associé à une plus grande probabilité d’être un gros fumeur : la probabilité de consommer de 1 à 7 cigarettes par jour commence à diminuer lorsque le revenu annuel dépasse 100 000 dollars, tandis que la probabilité de consommer >12 cigarettes par jour augmente avec le revenu pour devenir le résultat de tabagisme le plus courant lorsque le revenu est le plus élevé. Cela suggère que, parmi les fumeurs, les cigarettes sont traitées comme ce que les économistes appellent un bien normal, c’est-à-dire un bien dont la demande augmente lorsque le revenu augmente.
On peut voir dans cet exemple que l’effet du revenu sur la consommation de cigarettes est multiple. La commande ziologit permet de modéliser la susceptibilité au tabagisme ainsi que l’intensité du tabagisme, ce qui permet de mieux comprendre les facteurs influençant le comportement tabagique.
