Novinky ve 
Bayesovské průměrování modelů (BMA) pro lineární regresi
Proč si vybírat jen jeden model, když si můžete vypůjčit informace z mnoha? Nová sada bma provádí bayesovské průměrování modelů, aby zohlednila nejistotu modelů ve vaší analýze. Nejste si jisti, které prediktory zahrnout do lineárního regresního modelu? Pomocí nástroje bmaregress zjistíte, které prediktory jsou důležité. Proveďte výběr modelu, inferenci a predikci. Pomocí mnoha postestimulačních příkazů můžete zkoumat vlivné modely, složitost modelu, vhodnost modelu a predikční výkonnost, analýzu citlivosti na předpoklady o důležitosti modelů a prediktorů a další.
Nejdůležitější informace
-
Výběr modelu, odvozování a předpovídání
-
Výčet modelů a odběr vzorků MC3
-
Vždy zahrnuté a seskupené prediktory
-
Modelové priory: rovnoměrné, binomické, beta-binomické
-
Mnoho g-priorit, včetně hyper-g a robustních
-
Faktorové proměnné a operátory časových řad
-
Silná, slabá nebo žádná dědičnost pro interakce
-
Konvergence MCMC BMA
-
Posteriorní model a pravděpodobnosti zařazení
-
Prioritní a posteriorní rozdělení velikosti modelu
-
Posteriorní rozdělení parametrů modelu
-
Míry spojitosti pro dvojice prediktorů
-
Mapy s proměnlivou inkluzí
-
Logaritmické prediktivní skóre pro vhodnost modelu a výkonnost predikce
-
Analýza citlivosti
-
Předpověď
-
Podpora standardních bayesovských postestimulačních funkcí
-
Viz více Bayesovské průměrování modelu funkce
Úvod
Tradičně vybíráme model a provádíme inferenci a predikci podmíněnou tímto modelem. Naše výsledky obvykle nezohledňují nejistotu při výběru modelu, a mohou být proto příliš optimistické. Mohou být dokonce nesprávné, pokud se námi zvolený model podstatně liší od skutečného modelu generujícího data (DGM). V některých aplikacích můžeme mít o DGM silné teoretické nebo empirické důkazy. V jiných aplikacích, obvykle složité a nestabilní povahy, jako jsou aplikace v ekonomii, psychologii a epidemiologii, může být výběr jednoho spolehlivého modelu obtížný. Namísto spoléhání se pouze na jeden model se při průměrování modelů zprůměrují výsledky z více věrohodných modelů založených na pozorovaných datech. V BMA je „věrohodnost“ modelu popsána posteriorní modelovou pravděpodobností (PMP), která je určena pomocí základních bayesovských principů – Bayesovy věty – a je univerzálně aplikována na všechny analýzy dat. BMA lze použít k zohlednění nejistoty modelu při odhadu parametrů modelu a předpovědi nových pozorování, aby se předešlo příliš optimistickým závěrům. Je zvláště užitečná v aplikacích s několika pravděpodobnými modely, kde neexistuje jediný definitivní důvod pro výběr určitého modelu na úkor ostatních. Ale i v případě, že je konečným cílem výběr jediného modelu, může být BMA přínosná. Poskytuje principiální způsob, jak identifikovat důležité modely a prediktory v rámci uvažovaných tříd modelů. Její rámec umožňuje poznat vzájemné vztahy mezi různými prediktory z hlediska jejich tendence objevovat se v modelu společně, samostatně nebo nezávisle. Lze jej použít k vyhodnocení citlivosti konečných výsledků na různé předpoklady o důležitosti různých modelů a prediktorů. A poskytuje optimální predikce ve smyslu logaritmického skóre.
Sada bma
V regresním prostředí se nejistota modelu rovná nejistotě, které prediktory by měly být do modelu zahrnuty. K zohlednění výběru prediktorů v lineární regresi můžeme použít bmaregress. Prozkoumá modelový prostor buď vyčerpávajícím způsobem s možností výčtu, kdykoli je to proveditelné, nebo pomocí algoritmu složení modelu Markovovým řetězcem Monte Carlo (MCMC) (MC3) s možností vzorkování. Uvádí různé přehledy navštívených modelů a zahrnutých prediktorů a posteriorních rozdělení parametrů modelu. Umožňuje určit skupiny prediktorů, které mají být zahrnuty nebo vyloučeny z modelu společně, a prediktory, které jsou zahrnuty ve všech modelech. Poskytuje různá apriorní rozdělení pro modely v parametru mprior() a pro parametr g, který řídí smršťování regresních koeficientů směrem k nule, v parametru gprior(). Podporuje také faktorové proměnné a operátory časových řad a pomocí volby heredity() poskytuje několik způsobů, jak při odhadu zpracovávat interakce.
Podporováno je mnoho funkcí postestimace, které zahrnují i některé standardní funkce bayesovské postestimace.
| Příkaz | Popis |
|---|---|
|
Posteriorní vzorky regresních koeficientů |
|
|
grafy modelu a pravděpodobnosti |
|
|
grafy rozdělení velikosti modelu |
|
|
mapy s proměnlivou inkluzí |
|
|
grafy posteriorní hustoty koeficientů |
|
|
shrnutí posteriorního modelu a zahrnutí proměnných |
|
|
přehled velikosti modelu |
|
|
posteriorní pravděpodobnosti zařazení (PIP) pro prediktory |
|
|
míry spojitosti pro prediktory |
|
|
logaritmické prediktivní skóre (LPS) |
|
|
Předpovědi BMA |
|
|
Bayesovské grafické souhrny a diagnostika konvergence |
|
|
Bayesovské souhrnné statistiky pro parametry modelu a jejich funkce |
|
|
Bayesovské efektivní velikosti vzorků a související statistiky |
|
|
Bayesovské prediktivníp-hodnoty |
|
|
Bayesovské předpovědi |
Níže uvádíme prohlídku některých funkcí bma s využitím souboru dat. Tato datová sada obsahuje n=200
�=200 pozorování, p=10 �=10 ortogonální prediktory a výsledek y generovaný jako
y=0.5+1.2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
kde ϵ∼N(0,1)
�∼�(0,1) je standardní normální chybový člen.
. webuse bmaintro (Simulovaná data pro příklad BMA) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Výčet modelů
K dosazení lineární regrese BMA pro y na x1 až x10 použijeme bmaregress.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
S 10 prediktory a výchozí pevnou (referenční) hodnotou g-prior použije bmaregress výčet modelů a prozkoumá všech 210=1,024
210=1,024 možných modelů. Výchozí priorita modelu je beta-binomická s tvarovými parametry 1, která je rovnoměrná v celé velikosti modelu. A priori náš model BMA předpokládal malé smrštění regresních koeficientů směrem k nule, protože g/(1+g)=0.9950 �/(1+�)=0.9950 je blízké 1.
bmaregress identifikoval x2 a x10 jako velmi důležité prediktory – jejich posteriorní pravděpodobnosti zahrnutí (PIP) jsou v podstatě 1. Posteriorní střední odhady jejich regresních koeficientů jsou 1,2 (zaokrouhleno), resp. 5,1 a jsou velmi blízké skutečným hodnotám 1,2 a 5. Všechny ostatní prediktory mají mnohem nižší PIP a odhady koeficientů blízké nule. Naše zjištění BMA jsou v souladu se skutečným DGM.
Uložíme si aktuální výsledky odhadu pro pozdější použití. Stejně jako u ostatních bayesovských příkazů musíme nejprve uložit výsledky simulace, abychom mohli použít příkaz estimates store k uložení výsledků odhadu.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Věrohodné intervaly
bmaregress ve výchozím nastavení neuvádí věrohodné intervaly (CrI), protože vyžaduje potenciálně časově náročnou simulaci posteriorního vzorku parametrů modelu. Můžeme je však vypočítat po odhadu.
Nejprve použijeme bmacoefsample k vygenerování MCMC vzorku z posteriorního rozdělení parametrů modelu, které zahrnuje regresní koeficienty. Poté použijeme existující příkaz bayesstats summary k výpočtu posteriorních souhrnů vygenerovaného vzorku MCMC.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
95% CrI pro koeficient x2 je [1,05, 1,34] a pro x10 je [4,9, 5,26], což je v souladu s naším DGM.
Vlivné modely
Odhady koeficientů BMA jsou zprůměrovány pro 1 024 modelů. Je důležité prozkoumat, které modely mají vliv. Ke zkoumání PMP můžeme použít modely bmastats.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Není překvapením, že model, který obsahuje x2 i x10, má nejvyšší PMP, přibližně 63 %. Ve skutečnosti dva nejlepší modely odpovídají kumulativnímu PMP přibližně 77 %:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
K vykreslení kumulativního PMP můžeme použít bmagraph pmp.
. bmagraph pmp, cumulative

Příkaz ve výchozím nastavení vykreslí prvních 100 modelů, ale pokud chcete zobrazit více modelů, můžete zadat volbu top().
Důležité prediktory
Důležitost prediktorů můžeme vizuálně prozkoumat pomocí bmagraph varmap, který vytvoří mapu zahrnutí proměnných.
. bmagraph varmap Computing model probabilities ...

Modely x2 a x10 jsou zahrnuty ve všech 100 nejlepších modelech podle PMP. Jejich koeficienty jsou ve všech modelech kladné.
Rozdělení velikosti modelu
Složitost našeho modelu BMA můžeme prozkoumat pomocí bmastats msize a bmagraph msize k prozkoumání předběžného a následného rozdělení velikosti modelu.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
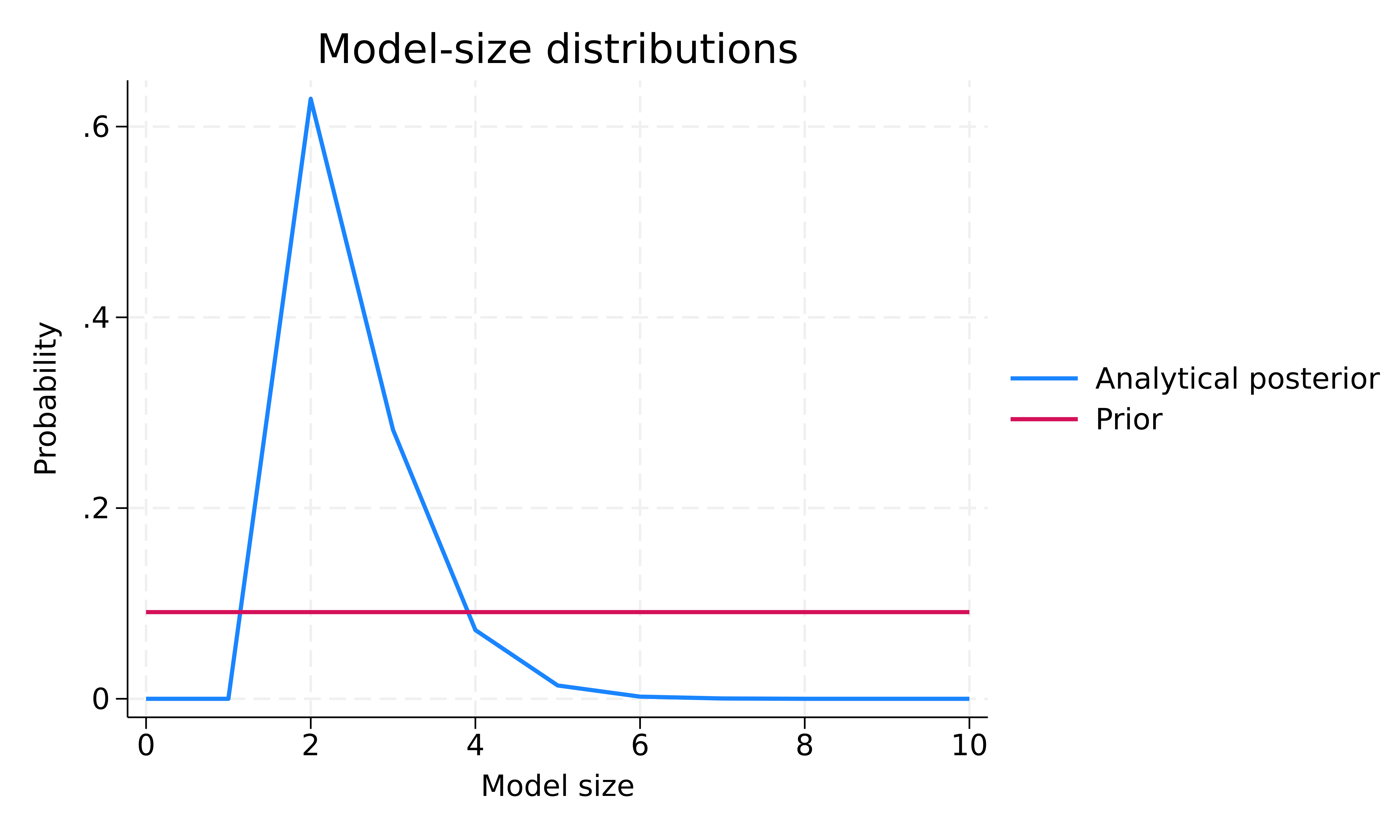
Předběžné rozdělení velikosti modelu je rovnoměrné pro velikost modelu. Posteriorní rozdělení velikosti modelu je zkosené doleva s modem přibližně 2. Prioritní průměrná velikost modelu je 5 a posteriorní 2,48. Na základě pozorovaných údajů má tedy BMA tendenci upřednostňovat menší modely se zhruba dvěma prediktory v průměru ve srovnání s naším apriorním předpokladem.
Posteriorní rozdělení koeficientů
Pomocí bmagraph coefdensity můžeme vykreslit posteriorní rozdělení regresních koeficientů.
. bmagraph coefdensity {x2} {x3}, combine
Tato rozdělení jsou směsí bodové hmotnosti v nule odpovídající pravděpodobnosti nezařazení prediktoru a spojité hustoty podmíněné zařazením. Pro koeficient x2 je pravděpodobnost nezařazení zanedbatelná, takže jeho posteriorní rozdělení je v podstatě spojitá, poměrně symetrická hustota se středem v 1,2. Pro koeficient x3 je kromě podmíněné spojité hustoty v bodě nula červená svislá čára odpovídající posteriorní pravděpodobnosti nezařazení zhruba 1-,2 = 0,8.
Předpověď BMA
bmapredict vytváří různé předpovědi BMA. Vypočítejme například posteriorní predikční průměry.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Můžeme také vypočítat prediktivní CrI, abychom odhadli nejistotu našich předpovědí. (To není možné u mnoha tradičních metod výběru modelu.) Všimněte si, že tyto prediktivní CrI zahrnují také nejistotu modelu. Abychom mohli vypočítat prediktivní CrI, musíme nejprve uložit posteriorní vzorek parametrů modelu MCMC.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Shrnujeme předpokládané výsledky:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Uváděné průměry za pozorování pro prediktivní průměry a dolní a horní 95% prediktivní hranice CrI vypadají vzhledem k pozorovanému výsledku y přiměřeně.
Informativní modelové priory
Jednou ze silných stránek metody BMA je možnost zahrnout předchozí informace o modelech a prediktorech. To nám umožňuje zkoumat citlivost výsledků na různé předpoklady o významu modelů a prediktorů. Předpokládejme, že máme spolehlivou informaci, že všechny prediktory kromě x2 a x10 mají menší pravděpodobnost vztahu k výsledku. Můžeme zadat například prioritu binomického modelu s nízkou prioritou pravděpodobnosti zahrnutí těchto prediktorů.
Abychom mohli později porovnat výkonnost modelů BMA mimo vzorek, rozdělili jsme náhodně vzorek na dvě části a model BMA jsme použili v prvním podvzorku. Výsledky z tohoto informativnějšího modelu BMA rovněž uložíme.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Důsledkem tohoto modelu prior je, že PIP všech nedůležitých prediktorů je nyní menší než 2 %.
Všimněte si, že při výběru jednoho modelu v podstatě fitujeme model BMA s velmi silnou prioritou, že všechny vybrané prediktory musí být zahrnuty s pravděpodobností 1. Můžeme například donutit bmaregress, aby do modelu zahrnul všechny proměnné:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Prediktivní výkonnost pomocí LPS
Pro porovnání uvažovaných modelů BMA jsme znovu sestavili náš výchozí model BMA s použitím prvního podvzorku a uložili výsledky odhadu.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Predikční výkonnost našich modelů BMA mimo vzorek můžeme porovnat pomocí nástroje bmastats lps, který vypočítá logaritmické predikční skóre (LPS) pro pozorování mimo vzorek.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Informativnější model bmareg_inf má o něco menší průměrnou hodnotu LPS, ale souhrny LPS jsou u všech modelů velmi podobné. Postup porovnání výkonnosti modelů BMA pomocí křížové validace naleznete v [BMA] bmastats lps.
Čištění
Během analýzy jsme vytvořili několik souborů dat. Již je nepotřebujeme, a proto je na závěr vymažeme. Můžete se však rozhodnout, že si je ponecháte, zejména pokud odpovídají potenciálně časově náročné závěrečné analýze.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
