New In 
Bayes-i modellátlagolás (BMA) lineáris regresszióhoz
Miért válasszon egyetlen modellt, amikor több modellből is kölcsönözhet információt? Az új bma csomag Bayes-modellátlagolást végez, hogy figyelembe vegye a modell bizonytalanságát az elemzés során. Bizonytalan abban, hogy mely prediktorokat vegye fel lineáris regressziós modelljébe? A bmaregress segítségével megtudhatja, hogy mely prediktorok fontosak. Végezzen modellválasztást, következtetést és előrejelzést. Használjon számos posztbecslési parancsot a befolyásoló modellek, a modell komplexitása, a modellillesztés és az előrejelzési teljesítmény, a modellek és prediktorok fontosságára vonatkozó feltételezésekkel kapcsolatos érzékenységvizsgálat és még sok más vizsgálat elvégzéséhez.
Kiemelt információk
-
Modellválasztás, következtetés és előrejelzés
-
Modellszámlálás és MC3 mintavétel
-
Mindig bevont és csoportosított prediktorok
-
Modell priorok: egységes, binomiális, béta-binomiális
-
Számos g-előfutár, beleértve a hiper-g és a robusztus
-
Tényezőváltozók és idősor-operátorok
-
Erős, gyenge vagy nem öröklődő kölcsönhatások
-
BMA MCMC konvergencia
-
Posterior modell és befogadási valószínűségek
-
Előzetes és utólagos modellméret-eloszlások
-
A modellparaméterek utólagos eloszlásai
-
A prediktorpárok közössége
-
Változó-bevonási térképek
-
Log prediktív pontszám a modell illeszkedésére és az előrejelzési teljesítményre vonatkozóan
-
Érzékenységi elemzés
-
Előrejelzés
-
A Bayes-féle standard utóbecslési funkciók támogatása
-
Lásd még Bayesi modellátlagolás funkciók
Bevezetés
Hagyományosan kiválasztunk egy modellt, és következtetést és előrejelzést végzünk e modell függvényében. Eredményeink általában nem veszik figyelembe a modell kiválasztásának bizonytalanságát, és így túlságosan optimisták lehetnek. Az eredmények akár helytelenek is lehetnek, ha a kiválasztott modell jelentősen eltér a valódi adatgeneráló modelltől (DGM). Egyes alkalmazásokban erős elméleti vagy empirikus bizonyítékokkal rendelkezhetünk a DGM-ről. Más, általában összetett és instabil jellegű alkalmazásokban, mint például a közgazdaságtan, a pszichológia és a járványtan, nehéz lehet egyetlen megbízható modell kiválasztása. Ahelyett, hogy csak egy modellre támaszkodnánk, a modellátlagolás a megfigyelt adatok alapján több plauzibilis modell eredményeit átlagolja. A BMA-ban a modell “plauzibilitását” a modell utólagos valószínűsége (posterior model probability, PMP) írja le, amelyet az alapvető Bayes-elvek – a Bayes-tétel – alapján határoznak meg, és minden adatelemzésre általánosan alkalmaznak. A BMA a modellparaméterek becslése és az új megfigyelések előrejelzése során a modell bizonytalanságának figyelembevételére használható, hogy elkerülhetők legyenek a túlzottan optimista következtetések. Különösen hasznos olyan alkalmazásokban, ahol több valószínűsíthető modell áll rendelkezésre, és ahol nincs egyetlen határozott ok sem arra, hogy egy adott modellt válasszunk a többivel szemben. De még akkor is hasznos lehet a BMA, ha egyetlen modell kiválasztása a végső cél. Elvi módszert biztosít a fontos modellek és prediktorok azonosítására a figyelembe vett modellosztályokon belül. A keretrendszer lehetővé teszi, hogy megismerje a különböző prediktorok közötti összefüggéseket aszerint, hogy hajlamosak-e együtt, külön-külön vagy egymástól függetlenül megjelenni egy modellben. Használható a végső eredmények érzékenységének értékelésére a különböző modellek és prediktorok fontosságára vonatkozó különböző feltételezésekkel szemben. És optimális előrejelzéseket biztosít a log-score értelemben.
A bma suite
Regressziós környezetben a modell bizonytalansága azt a bizonytalanságot jelenti, hogy mely prediktorokat kell bevonni a modellbe. A bmaregress segítségével figyelembe vehetjük a prediktorok kiválasztását egy lineáris regresszióban. A modellteret vagy kimerítően vizsgálja a felsorolás opcióval, amikor csak lehetséges, vagy a Markov-lánc Monte Carlo (MCMC) modellkompozíció (MC3) algoritmus segítségével a mintavétel opcióval. Különböző összefoglalókat ad a meglátogatott modellekről és a bevont prediktorokról, valamint a modellparaméterek utólagos eloszlásáról. Lehetővé teszi a modellbe együttesen bevonandó vagy kizárandó prediktorcsoportok, valamint az összes modellben szereplő prediktorcsoportok megadását. Különböző előzetes eloszlásokat biztosít a modellekhez az mprior() opcióban és a g paraméterhez, amely a regressziós együtthatók nullára zsugorodását szabályozza, a gprior() opcióban. Támogatja továbbá a faktorváltozókat és az idősor-operátorokat, és a heredity() opció segítségével többféleképpen kezeli a becslés során fellépő kölcsönhatásokat.
Számos támogatott utóbecslési funkció van, amelyek között a Bayes-féle standard utóbecslési funkciók egy része is megtalálható.
| Parancs | Leírás |
|---|---|
|
A regressziós együtthatók utólagos mintái |
|
|
modell-valószínűségi ábrák |
|
|
modellméret-eloszlási grafikonok |
|
|
változó-bevonási térképek |
|
|
koefficiens poszterior sűrűség ábrák |
|
|
utólagos modell és változó-bevonási összefoglalók |
|
|
modellméret-összefoglaló |
|
|
a prediktorokra vonatkozó utólagos befogadási valószínűségek (PIP) |
|
|
a prediktorokra vonatkozó együttes intézkedések |
|
|
log prediktív pontszám (LPS) |
|
|
BMA előrejelzések |
|
|
Bayes-féle grafikus összefoglalók és konvergencia-diagnosztika |
|
|
A modellparaméterek és függvényeik Bayes-összefoglaló statisztikái |
|
|
Bayes-féle effektív mintanagyságok és kapcsolódó statisztikák |
|
|
Bayes-előrejelző p-értékek |
|
|
Bayes-előrejelzések |
Az alábbiakban néhány bma jellemzőt mutatunk be egy játékadatkészlet segítségével. Ez az adathalmaz n=200
�=200 megfigyelést, p=10 �=10 ortogonális prediktort, és az y eredményt a következő módon generáltuk
y=0.5+1.2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
ahol ϵ∼N(0,1)
�∼�(0,1) egy standard normál hibatermet jelent.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Modell felsorolás
A bmaregress segítségével BMA lineáris regressziót illesztünk az y-ra x1-től x10-ig.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
10 prediktorral és az alapértelmezett fix (benchmark) g-priorral a bmaregress a modell felsorolását használja, és megvizsgálja az összes 210=1,024
210=1,024 lehetséges modellt. Az alapértelmezett modellprioritás béta-binomiális, 1 alakú alakparaméterekkel, ami a modellméretre nézve egységes. A priori a BMA-modellünk feltételezte a regressziós együtthatók kis mértékű zsugorodását a nulla felé, mivel g/(1+g)=0,9950 �/(1+�)=0,9950 közel 1.
A bmaregress az x2-t és az x10-et nagyon fontos prediktorként azonosította – ezek utólagos befogadási valószínűsége (PIP) lényegében 1. A regressziós együtthatóik utólagos átlagos becslései 1,2 (kerekítve), illetve 5,1, és nagyon közel vannak az 1,2 és 5 valódi értékekhez. Az összes többi prediktor PIP-értéke sokkal alacsonyabb, és az együttható becslései közel vannak a nullához. A BMA-eredményeink összhangban vannak a valódi DGM-mel.
Tároljuk el a jelenlegi becslési eredményeinket későbbi felhasználásra. Más Bayes-parancsokhoz hasonlóan először el kell mentenünk a szimulációs eredményeket, mielőtt a becslések tárolása parancsot használhatnánk a becslési eredmények tárolására.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Hiteles intervallumok
A bmaregress alapértelmezés szerint nem közöl hiteles intervallumokat (CrI), mivel a modellparaméterek utólagos mintájának potenciálisan időigényes szimulációját igényli. A becslés után azonban kiszámíthatjuk őket.
Először a bmacoefsample segítségével MCMC-mintát hozunk létre a modellparaméterek utólagos eloszlásából, amely magában foglalja a regressziós együtthatókat is. Ezután a meglévő bayesstats summary parancsot használjuk a generált MCMC-minta utólagos összegzéseinek kiszámításához.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
Az x2 együttható 95%-os CrI-je [1,05, 1,34], az x10-é pedig [4,9, 5,26], ami összhangban van a DGM-ünkkel.
Befolyásoló modellek
A BMA-koefficiensbecslések átlaga 1024 modellre vonatkozik. Fontos megvizsgálni, hogy mely modellek befolyásosak. A bmastats modellek segítségével feltárhatjuk a PMP-ket.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Nem meglepő módon az x2-t és x10-et is tartalmazó modellnek van a legmagasabb, 63% körüli PMP-je. Valójában a két legjobb modell körülbelül 77%-os kumulatív PMP-nek felel meg:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
A bmagraph pmp segítségével ábrázolhatjuk a kumulatív PMP-t.
. bmagraph pmp, cumulative

A parancs alapértelmezés szerint az első 100 modellt ábrázolja, de megadhatja a top() opciót, ha több modellt szeretne látni.
Fontos előrejelzők
A prediktorok fontosságát vizuálisan is felfedezhetjük a bmagraph varmap segítségével, amellyel egy változó-bevonási térképet készíthetünk.
. bmagraph varmap Computing model probabilities ...

Az x2 és az x10 a PMP szerint rangsorolt top 100 modellben szerepel. Együtthatóik minden modellben pozitívak.
Modellméret-eloszlás
A BMA-modellünk komplexitását a bmastats msize és a bmagraph msize segítségével vizsgálhatjuk meg a modellméret előzetes és utólagos eloszlásának feltárásához.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
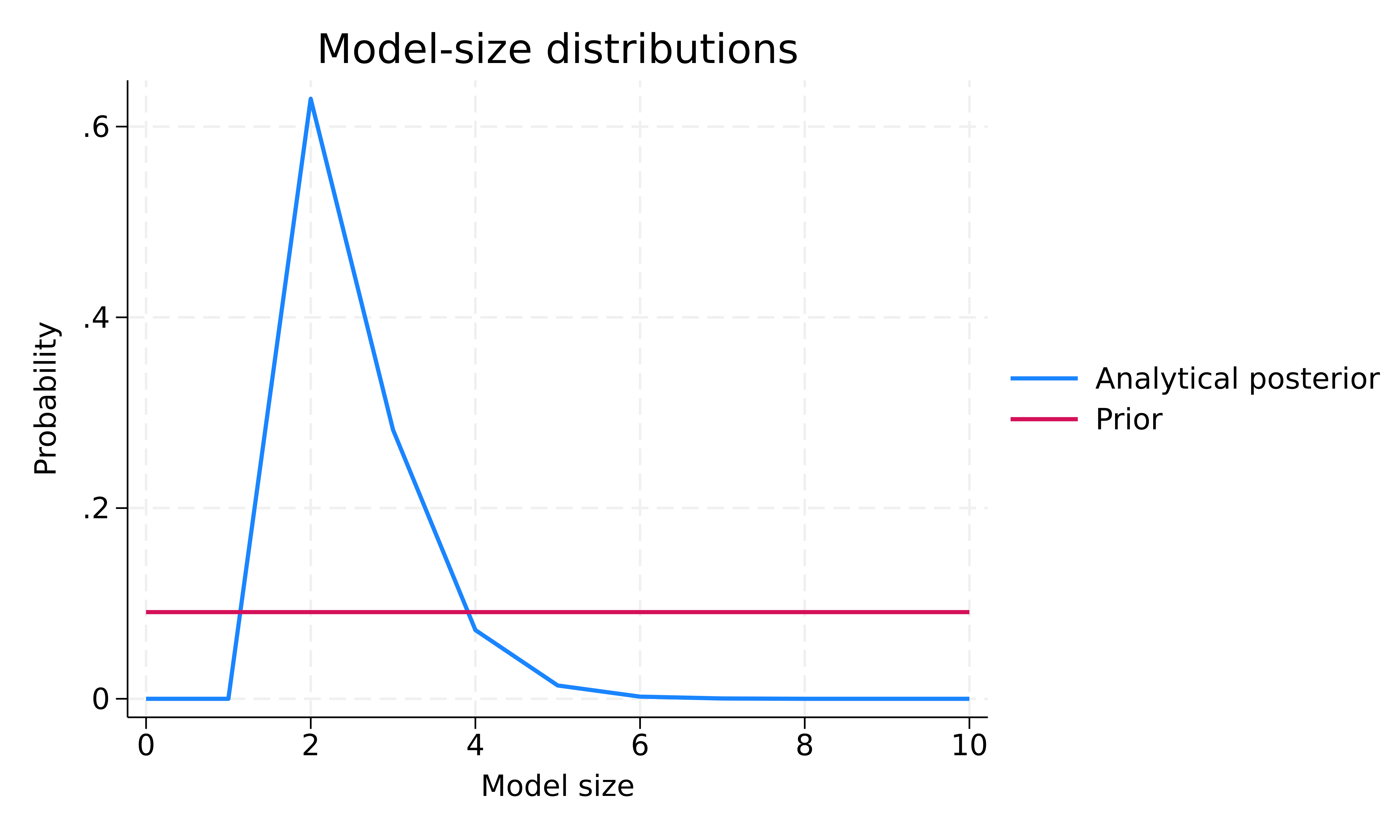
Az előzetes modellméret-eloszlás egyenletes a modellméretre. Az utólagos modellméret-eloszlás balra ferde, a módusz körülbelül 2. Az előzetes átlagos modellméret 5, az utólagos pedig 2,48. A megfigyelt adatok alapján tehát a BMA az a priori feltételezésünkhöz képest a kisebb, átlagosan nagyjából két prediktort tartalmazó modelleket részesíti előnyben.
Az együtthatók utólagos eloszlása
A bmagraph coefdensity segítségével ábrázolhatjuk a regressziós együtthatók utólagos eloszlásait.
. bmagraph coefdensity {x2} {x3}, combine
Ezek az eloszlások egy nullpontos tömeg keverékei, amely megfelel a prediktor be nem vonásának valószínűségének és egy folytonos sűrűségnek, amely a bevonás függvénye. Az x2 együttható esetében a be nem vonás valószínűsége elhanyagolható, így az utólagos eloszlása lényegében egy folytonos, meglehetősen szimmetrikus sűrűség, amelynek középpontja 1,2. Az x3 együttható esetében a feltételes folytonos sűrűségen kívül egy piros függőleges vonal is van a nullánál, amely a be nem vonás utólagos valószínűségének felel meg, ami nagyjából 1-,2 = 0,8.
BMA előrejelzés
A bmapredict különböző BMA-előrejelzéseket készít. Számítsuk ki például az utólagos prediktív középértékeket.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Előrejelző CrI-ket is kiszámíthatunk, hogy megbecsüljük az előrejelzéseinkkel kapcsolatos bizonytalanságot. (Ez sok hagyományos modellválasztási módszerrel nem áll rendelkezésre.) Vegyük észre, hogy ezek a prediktív CrI-k a modell bizonytalanságát is magukban foglalják. A prediktív CrI-k kiszámításához először el kell mentenünk az utólagos MCMC modellparaméter-mintát.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Összefoglaljuk az előre jelzett eredményeket:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
A prediktív átlagok és az alsó és felső 95%-os prediktív CrI-határok megfigyelésekre vonatkozó átlagai ésszerűnek tűnnek a megfigyelt y eredményhez képest.
Informatív modell priorok
A BMA egyik erőssége, hogy képes a modellekre és prediktorokra vonatkozó előzetes információk beépítésére. Ez lehetővé teszi, hogy megvizsgáljuk az eredmények érzékenységét a modellek és prediktorok fontosságára vonatkozó különböző feltételezésekre. Tegyük fel, hogy megbízható információval rendelkezünk arról, hogy az x2 és x10 kivételével minden prediktor kevésbé valószínű, hogy kapcsolatban van a kimenettel. Megadhatunk például egy binomiális modell priorját alacsony előzetes bevonási valószínűséggel ezekre a prediktorokra.
A BMA-modellek mintán kívüli teljesítményének későbbi összehasonlításához véletlenszerűen két részre osztottuk a mintánkat, és a BMA-modellt az első részmintára illesztettük. Ennek az informatívabb BMA-modellnek az eredményeit is elmentjük.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Ennek a modell-előzetesnek az a hatása, hogy az összes nem fontos prediktor PIP-je most kevesebb, mint 2%.
Vegyük észre, hogy amikor kiválasztunk egy modellt, lényegében egy BMA-modellt illesztünk be egy nagyon erős priorral, amely szerint minden kiválasztott prediktort 1 valószínűséggel kell bevonni. Például kényszeríthetjük a bmaregress-t, hogy minden változót bevegyen a modellbe:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Előrejelző teljesítmény az LPS használatával
A figyelembe vett BMA-modellek összehasonlítása érdekében az alapértelmezett BMA-modellünket az első részmintát felhasználva újrateszteljük, és a becslési eredményeket tároljuk.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Összehasonlíthatjuk a BMA-modelleink mintán kívüli előrejelző teljesítményét a bmastats lps segítségével, amely kiszámítja a log prediktív pontszámot (LPS) a mintán kívüli megfigyelésekre.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Az informatívabb bmareg_inf modell átlagos LPS-értéke valamivel kisebb, de az összes modell LPS-összegzése nagyon hasonló. Lásd [BMA] bmastats lps a BMA-modellek teljesítményének kereszthitelesítéssel történő összehasonlításához.
Tisztítás
Elemzésünk során több adatkészletet generáltunk. Ezekre már nincs szükségünk, ezért a végén töröljük őket. Ön azonban dönthet úgy, hogy megtartja őket, különösen, ha egy potenciálisan időigényes végső elemzésnek felelnek meg.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
