New In 
Байесовское усреднение моделей (БМА) для линейной регрессии
Зачем выбирать только одну модель, если можно взять информацию из многих? Новый пакет bma выполняет байесовское усреднение моделей для учета неопределенности модели в анализе. Не знаете, какие предикторы включить в модель линейной регрессии? Используйте bmaregress, чтобы выяснить, какие предикторы важны. Выполните выбор модели, вывод и предсказание. Используйте множество команд постоценки для изучения влиятельных моделей, сложности моделей, их соответствия и предсказательной эффективности, анализа чувствительности к предположениям о важности моделей и предикторов и т.д.
Основные моменты
-
Выбор модели, вывод и прогнозирование
-
Перечисление моделей и выборка MC3
-
Всегда включенные и сгруппированные предикторы
-
Приоры модели: равномерный, биномиальный, бета-биномиальный
-
Многие g-приоры, включая hyper-g и robust
-
Факторные переменные и операторы временных рядов
-
Сильная, слабая или отсутствие наследственности по взаимодействию
-
Сходимость BMA MCMC
-
Постреляционная модель и вероятности включения
-
Приоритетные и апостериорные распределения размеров моделей
-
Апостериорные распределения параметров модели
-
Меры связности для пар предикторов
-
Карты с переменным включением
-
Log predictive-score для оценки пригодности модели и эффективности прогнозирования
-
Анализ чувствительности
-
Прогноз
-
Поддержка стандартных функций байесовской постоценки
-
См. подробнее Байесовское усреднение моделей особенности
Введение
Традиционно мы выбираем модель и выполняем вывод и предсказание в зависимости от этой модели. Наши результаты, как правило, не учитывают неопределенность при выборе модели и поэтому могут быть излишне оптимистичными. Они могут быть даже неверными, если выбранная нами модель существенно отличается от истинной модели генерации данных (МГД). В некоторых приложениях мы можем располагать убедительными теоретическими или эмпирическими данными о DGM. В других приложениях, обычно имеющих сложную и нестабильную природу, таких как экономика, психология и эпидемиология, выбор одной надежной модели может быть затруднен. Вместо того чтобы полагаться только на одну модель, усреднение моделей приводит к усреднению результатов по нескольким правдоподобным моделям, основанным на наблюдаемых данных. В BMA «правдоподобность» модели описывается апостериорной вероятностью модели (PMP), которая определяется с использованием фундаментальных принципов Байеса — теоремы Байеса — и применяется универсально для всех анализов данных. BMA может использоваться для учета неопределенности модели при оценке параметров модели и прогнозировании новых наблюдений, что позволяет избежать слишком оптимистичных выводов. Она особенно полезна в приложениях с несколькими правдоподобными моделями, когда нет однозначной причины для выбора конкретной модели, а не других. Но даже если выбор одной модели является конечной целью, BMA может оказаться полезным. Она предоставляет принципиальный способ выявления важных моделей и предикторов в рамках рассматриваемых классов моделей. Его структура позволяет изучать взаимосвязи между различными предикторами с точки зрения их склонности появляться в модели вместе, отдельно или независимо друг от друга. С его помощью можно оценить чувствительность конечных результатов к различным предположениям о важности различных моделей и предикторов. И обеспечивает оптимальные прогнозы в смысле log-score.
Комплект bma
В регрессионных условиях неопределенность модели сводится к неопределенности того, какие предикторы должны быть включены в модель. Для учета выбора предикторов в линейной регрессии можно использовать bmaregress. Он исследует пространство моделей либо исчерпывающим образом с помощью опции перечисления, когда это возможно, либо с помощью алгоритма составления моделей с марковской цепью Монте-Карло (MCMC) с опцией выборки (MC3). При этом выдаются различные сводки по посещенным моделям и включенным в них предикторам, а также постерные распределения параметров моделей. Позволяет задавать группы предикторов, включаемых или исключаемых из модели вместе, а также включаемых во все модели. В опции mprior() предусмотрены различные предшествующие распределения для моделей, а в опции gprior() — для параметра g, управляющего уменьшением коэффициентов регрессии к нулю. Поддерживаются факторные переменные и операторы временных рядов, а также несколько способов обработки взаимодействий в процессе оценки с помощью опции heredity().
Поддерживается множество функций постоценки, в том числе и некоторые стандартные функции байесовской постоценки.
| Команда | Описание |
|---|---|
|
Последующие выборки коэффициентов регрессии |
|
|
графики модель-вероятность |
|
|
графики распределения размеров моделей |
|
|
карты включения переменных |
|
|
графики плотности апостериорного распределения коэффициентов |
|
|
апостериорная модель и сводки по включению переменных |
|
|
краткое описание типоразмеров |
|
|
апостериорные вероятности включения (PIPs) для предикторов |
|
|
меры совместности для предикторов |
|
|
log predictive-score (LPS) |
|
|
Прогнозы BMA |
|
|
Байесовские графические обобщения и диагностика сходимости |
|
|
Байесовские суммарные статистики для параметров моделей и их функций |
|
|
Байесовские эффективные размеры выборок и связанные с ними статистики |
|
|
Байесовские прогностические p-значения |
|
|
Байесовские прогнозы |
Давайте посмотрим, как это работает
-> Перечисление моделей -> Достоверные интервалы -> Влиятельные модели -> Важные предикторы ->Распределение моделей по размерам -> Апостериорные распределения коэффициентов -> Прогноз BMA -> Информативность модельных приматов -> Прогнозные характеристики с использованием LPS -> Очистка
Ниже мы приводим описание некоторых функций bma на примере игрушечного набора данных. Этот набор содержит n=200
�=200 наблюдений, p=10 �=10 ортогональных предикторов, а результат y формируется как
y=0,5+1,2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
где ϵ∼N(0,1)
�∼�(0,1) — стандартный нормальный член ошибки.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Перечисление моделей
С помощью bmaregress мы настраиваем BMA-линейную регрессию y на x1 — x10.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
При 10 предикторах и фиксированном (эталонном) значении g-prior по умолчанию bmaregress использует перечисление моделей и исследует все 210=1,024
210=1 024 возможных моделей. По умолчанию используется бета-биномиальный приоритет модели с параметрами формы, равными 1, который равномерно распределяется по размеру модели. Априори в нашей модели BMA предполагалось незначительное уменьшение коэффициентов регрессии к нулю, так как g/(1+g)=0,9950 �/(1+�)=0,9950 близко к 1.
bmaregress определил x2 и x10 как очень важные предикторы — их апостериорные вероятности включения (PIP) практически равны 1. Апостериорные средние оценки их коэффициентов регрессии составляют, соответственно, 1,2 (округленно) и 5,1 и очень близки к истинным значениям 1,2 и 5. Все остальные предикторы имеют гораздо более низкие PIP и оценки коэффициентов, близкие к нулю. Полученные нами результаты BMA согласуются с истинным значением DGM.
Сохраним наши текущие результаты оценки для последующего использования. Как и в других байесовских командах, прежде чем использовать команду estimates store для сохранения результатов оценки, необходимо сначала сохранить результаты моделирования.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Достоверные интервалы
По умолчанию bmaregress не выдает доверительные интервалы (ДПИ), поскольку это требует потенциально трудоемкого моделирования апостериорной выборки параметров модели. Однако мы можем вычислить их после оценки.
Сначала мы используем bmacoefsample для генерации MCMC-выборки из апостериорного распределения параметров модели, включающих коэффициенты регрессии. Затем мы используем существующую команду bayesstats summary для вычисления апостериорных сумм сгенерированной MCMC-выборки.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
95%-ный критерий для коэффициента x2 составляет [1,05, 1,34], а для x10 — [4,9, 5,26], что согласуется с нашей ДГМ.
Влиятельные модели
Оценки коэффициентов BMA усреднены по 1024 моделям. Важно выяснить, какие модели являются влиятельными. Для этого мы можем использовать модели bmastats, чтобы исследовать ПМП.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Неудивительно, что модель, содержащая и x2, и x10, имеет самый высокий PMP — около 63%. Фактически, две лучшие модели соответствуют суммарному PMP около 77%:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
Мы можем использовать bmagraph pmp для построения графика кумулятивного PMP.
. bmagraph pmp, cumulative

По умолчанию команда выводит на экран первые 100 моделей, но можно указать опцию top(), если вы хотите увидеть больше моделей.
Важные предикторы
Мы можем наглядно изучить важность предикторов, используя bmagraph varmap для создания карты включения переменных.
. bmagraph varmap Computing model probabilities ...

x2 и x10 входят во все 100 лучших моделей, ранжированных по PMP. Их коэффициенты положительны во всех моделях.
Распределение моделей по размерам
Мы можем исследовать сложность нашей модели BMA с помощью bmastats msize и bmagraph msize для изучения предшествующего и последующего распределений размеров модели.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
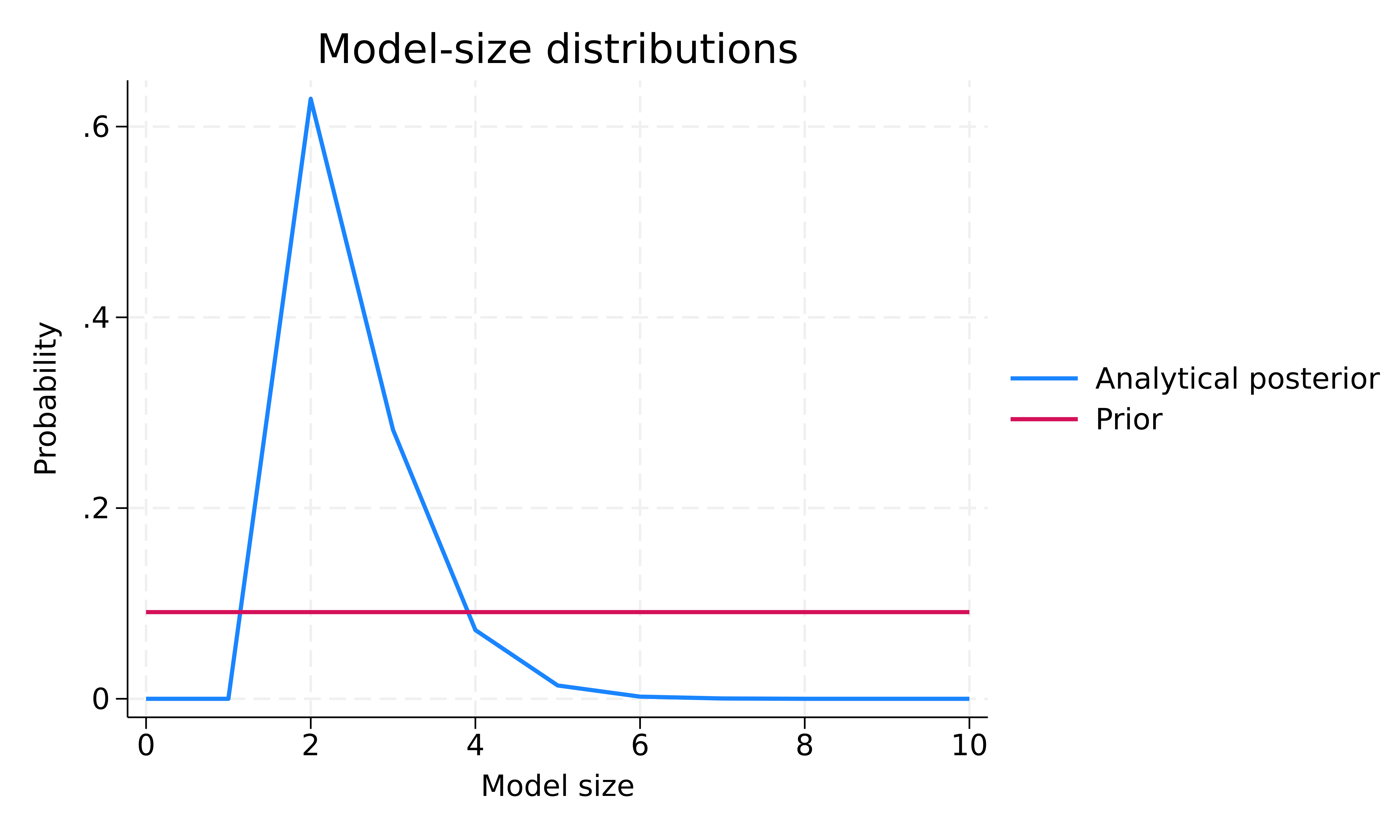
Предварительное распределение размера модели равномерно по размеру модели. Апостериорное распределение размера модели имеет перекос влево с модой около 2. Средний размер модели в априорном случае равен 5, а в апостериорном — 2,48. Таким образом, исходя из наблюдаемых данных, BMA склоняется к меньшим моделям с двумя предикторами в среднем по сравнению с нашим априорным предположением.
Апостериорные распределения коэффициентов
С помощью bmagraph coefdensity можно построить апостериорные распределения коэффициентов регрессии.
. bmagraph coefdensity {x2} {x3}, combine
Эти распределения представляют собой смесь точечной массы в нуле, соответствующей вероятности невключения предиктора, и непрерывной плотности, обусловленной включением. Для коэффициента x2 вероятность невключения пренебрежимо мала, поэтому его апостериорное распределение представляет собой, по сути, непрерывную, достаточно симметричную плотность с центром в точке 1,2. Для коэффициента x3, помимо условной непрерывной плотности, в нулевой точке имеется красная вертикальная линия, соответствующая апостериорной вероятности невключения, равной примерно 1-,2 = 0,8.
Прогноз BMA
bmapredict выдает различные прогнозы BMA. Например, вычислим апостериорные прогностические средства.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Мы также можем рассчитать прогностические КрИ для оценки неопределенности наших прогнозов. (Заметим, что эти прогнозные КрИ также включают в себя неопределенность модели. Для вычисления прогнозируемого КрИ необходимо сначала сохранить апостериорную MCMC-выборку параметров модели.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Мы обобщаем прогнозируемые результаты:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Приведенные средние значения по наблюдениям для прогностических средств, а также нижняя и верхняя 95%-ные прогностические границы CrI выглядят разумными относительно наблюдаемого результата y.
Информативность модельных приматов
Одним из достоинств BMA является возможность учета предварительной информации о моделях и предикторах. Это позволяет исследовать чувствительность результатов к различным предположениям о важности моделей и предикторов. Предположим, что у нас есть достоверная информация о том, что все предикторы, кроме x2 и x10, с меньшей вероятностью связаны с результатом. Мы можем задать, например, предварительную биномиальную модель с низкой вероятностью включения этих предикторов.
Для сравнения вневыборочных характеристик моделей BMA в дальнейшем мы случайным образом разделили нашу выборку на две части и подогнали модель BMA к первой подвыборке. Мы также сохраняем результаты, полученные с помощью этой более информативной BMA-модели.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Эффект этого приоритета модели заключается в том, что PIP всех неважных предикторов теперь составляет менее 2%.
Обратите внимание, что при выборе одной модели мы, по сути, подгоняем BMA-модель с очень сильным приоритетом, согласно которому все выбранные предикторы должны быть включены с вероятностью 1. Например, мы можем заставить bmaregress включить в модель все переменные:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Эффективность прогнозирования с использованием LPS
Для сравнения рассмотренных моделей BMA мы переделали нашу стандартную модель BMA, используя первую подвыборку, и сохранили результаты оценки.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Мы можем сравнить предсказательную эффективность наших BMA-моделей за пределами выборки, используя bmastats lps для вычисления логарифмической предсказательной оценки (LPS) для наблюдений за пределами выборки.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Более информативная модель bmareg_inf имеет несколько меньшее среднее значение LPS, но итоговые значения LPS для всех моделей очень близки. О том, как сравнить производительность моделей BMA с помощью перекрестной валидации, см. в [BMA] bmastats lps.
Очистка
В процессе анализа мы создали несколько наборов данных. Они нам больше не нужны, поэтому в конце мы их удаляем. Однако вы можете решить сохранить их, особенно если они соответствуют потенциально трудоемкому заключительному анализу.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
