New In 
Bayes’sche Modell-Mittelung (BMA) für lineare Regression
Warum nur ein Modell auswählen, wenn man Informationen von vielen Modellen nutzen kann? Die neue bma-Suite führt eine Bayes’sche Modell-Mittelwertbildung durch, um die Modellunsicherheit in Ihrer Analyse zu berücksichtigen. Sind Sie unsicher, welche Prädiktoren Sie in Ihr lineares Regressionsmodell aufnehmen sollen? Verwenden Sie bmaregress, um herauszufinden, welche Prädiktoren wichtig sind. Führen Sie Modellwahl, Inferenz und Vorhersage durch. Verwenden Sie zahlreiche Befehle zur Nachschätzung, um einflussreiche Modelle, Modellkomplexität, Modellanpassung und Vorhersageleistung, Sensitivitätsanalysen zu den Annahmen über die Bedeutung von Modellen und Prädiktoren und vieles mehr zu untersuchen.
Höhepunkte
-
Modellwahl, Schlussfolgerungen und Vorhersagen
-
Modellaufzählung und MC3-Probenahme
-
Immer enthaltene und gruppierte Prädiktoren
-
Modellprioritäten: Uniform, Binomial, Beta-Binomial
-
Viele g-Prioritäten, einschließlich hyper-g und robust
-
Faktorvariablen und Zeitreihenoperatoren
-
Starke, schwache oder keine Vererbung von Wechselwirkungen
-
BMA MCMC-Konvergenz
-
Posteriores Modell und Einschlusswahrscheinlichkeiten
-
Prior- und Posterior-Verteilung der Modellgröße
-
Posterior-Verteilungen der Modellparameter
-
Gemeinsamkeitsmaße für Paare von Prädiktoren
-
Karten mit variablem Einschluss
-
Logarithmischer Vorhersage-Score für Modellanpassung und Vorhersageleistung
-
Sensitivitätsanalyse
-
Vorhersage
-
Unterstützung der standardmäßigen Bayes’schen Postestimation
-
Mehr sehen Bayes’sche Modell-Mittelung merkmale
Einführung
Traditionell wählen wir ein Modell aus und führen Schlussfolgerungen und Vorhersagen auf der Grundlage dieses Modells durch. Unsere Ergebnisse berücksichtigen in der Regel nicht die Unsicherheit bei der Auswahl eines Modells und können daher übermäßig optimistisch sein. Sie können sogar falsch sein, wenn sich das von uns gewählte Modell erheblich von dem wahren datengenerierenden Modell (DGM) unterscheidet. Bei einigen Anwendungen haben wir vielleicht starke theoretische oder empirische Beweise für das DGM. Bei anderen Anwendungen, die in der Regel komplexer und instabiler Natur sind, wie z. B. in den Bereichen Wirtschaft, Psychologie und Epidemiologie, kann die Auswahl eines zuverlässigen Modells schwierig sein. Anstatt sich auf ein einziges Modell zu stützen, werden bei der Modell-Mittelwertbildung die Ergebnisse über mehrere plausible Modelle auf der Grundlage der beobachteten Daten gemittelt. Bei der BMA wird die „Plausibilität“ des Modells durch die posteriore Modellwahrscheinlichkeit (PMP) beschrieben, die anhand der grundlegenden Bayes’schen Prinzipien – dem Bayes-Theorem – bestimmt und universell auf alle Datenanalysen angewendet wird. Die BMA kann verwendet werden, um die Modellunsicherheit bei der Schätzung von Modellparametern und der Vorhersage neuer Beobachtungen zu berücksichtigen, um zu optimistische Schlussfolgerungen zu vermeiden. Sie ist besonders nützlich bei Anwendungen mit mehreren plausiblen Modellen, bei denen es keinen eindeutigen Grund gibt, ein bestimmtes Modell den anderen vorzuziehen. Aber auch wenn die Wahl eines einzigen Modells das Endziel ist, kann die BMA von Nutzen sein. Sie bietet eine prinzipielle Methode zur Identifizierung wichtiger Modelle und Prädiktoren innerhalb der betrachteten Modellklassen. Ihr Rahmen ermöglicht es Ihnen, die Wechselbeziehungen zwischen verschiedenen Prädiktoren in Bezug auf ihre Tendenz, zusammen, getrennt oder unabhängig voneinander in einem Modell aufzutreten, zu erkennen. Es kann verwendet werden, um die Empfindlichkeit der Endergebnisse gegenüber verschiedenen Annahmen über die Bedeutung verschiedener Modelle und Prädiktoren zu bewerten. Und es liefert optimale Vorhersagen im Sinne des Log-Score.
Die bma-Suite
In einer Regressionsumgebung ist die Modellunsicherheit gleichbedeutend mit der Unsicherheit darüber, welche Prädiktoren in ein Modell aufgenommen werden sollten. Wir können bmaregress verwenden, um die Auswahl der Prädiktoren in einer linearen Regression zu berücksichtigen. Es untersucht den Modellraum entweder erschöpfend mit der Aufzählungsoption, wann immer dies möglich ist, oder unter Verwendung des Markov-Chain-Monte-Carlo (MCMC)-Modellkompositionsalgorithmus (MC3) mit der Sampling-Option. Es liefert verschiedene Zusammenfassungen der besuchten Modelle und der einbezogenen Prädiktoren sowie der Posteriorverteilungen der Modellparameter. Sie können Gruppen von Prädiktoren angeben, die in ein Modell aufgenommen oder aus diesem ausgeschlossen werden sollen, und solche, die in allen Modellen enthalten sind. Es bietet verschiedene Prior-Verteilungen für Modelle in der Option mprior() und für den Parameter g, der die Schrumpfung der Regressionskoeffizienten gegen Null steuert, in der Option gprior(). Es unterstützt auch Faktorvariablen und Zeitreihenoperatoren und bietet mehrere Möglichkeiten zur Behandlung von Interaktionen während der Schätzung mit der Option heredity().
Es gibt viele unterstützte Postestimationsfunktionen, zu denen auch einige der standardmäßigen Bayes’schen Postestimationsfunktionen gehören.
| Befehl | Beschreibung |
|---|---|
|
Posteriore Stichproben der Regressionskoeffizienten |
|
|
Modell-Wahrscheinlichkeits-Diagramme |
|
|
Modellgrößenverteilungsdiagramme |
|
|
Karten mit variablem Einschluss |
|
|
Koeffiziente Posterior-Dichte-Diagramme |
|
|
Zusammenfassungen des posterioren Modells und der eingeschlossenen Variablen |
|
|
Modell-Größenübersicht |
|
|
nachträgliche Einschlusswahrscheinlichkeiten (PIPs) für Prädiktoren |
|
|
Verbindlichkeitsmaße für Prädiktoren |
|
|
log predictive-score (LPS) |
|
|
BMA-Prognosen |
|
|
Bayessche grafische Zusammenfassungen und Konvergenzdiagnostik |
|
|
Bayessche zusammenfassende Statistiken für Modellparameter und ihre Funktionen |
|
|
Effektive Bayes’sche Stichprobengrößen und verwandte Statistiken |
|
|
Bayessche prädiktive p-Werte |
|
|
Bayes’sche Vorhersagen |
Wir wollen sehen, wie es funktioniert
-> Modell-Aufzählung -> Glaubwürdige Intervalle -> Einflussreiche Modelle -> Wichtige Prädiktoren ->Verteilung der Modellgröße -> Posterior-Verteilung der Koeffizienten -> BMA-Vorhersage -> Informative Modellprioritäten -> Vorhersageleistung mit LPS -> Aufräumen
Im Folgenden stellen wir einige bma-Merkmale anhand eines Spielzeugdatensatzes vor. Dieser Datensatz enthält n=200
�=200 Beobachtungen, p=10 �=10 orthogonale Prädiktoren und das Ergebnis y wird generiert als
y=0,5+1,2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
wobei ϵ∼N(0,1)
�∼�(0,1) ein standardnormaler Fehlerterm ist.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Aufzählung der Modelle
Wir verwenden bmaregress, um eine lineare BMA-Regression von y auf x1 bis x10 durchzuführen.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
Bei 10 Prädiktoren und der Standardeinstellung g-prior (Benchmark) verwendet bmaregress die Modellaufzählung und untersucht alle 210=1.024
210=1.024 mögliche Modelle. Der Standardmodell-Prior ist beta-binomial mit Formparametern von 1, was für die Modellgröße einheitlich ist. A priori nahm unser BMA-Modell eine geringe Schrumpfung der Regressionskoeffizienten gegen Null an, da g/(1+g)=0,9950 �/(1+�)=0,9950 nahe bei 1 liegt.
bmaregress identifizierte x2 und x10 als sehr wichtige Prädiktoren – ihre posterioren Inklusionswahrscheinlichkeiten (PIPs) liegen im Wesentlichen bei 1. Die posterioren Mittelwertschätzungen ihrer Regressionskoeffizienten betragen 1,2 (gerundet) bzw. 5,1 und liegen sehr nahe an den wahren Werten von 1,2 bzw. 5. Alle anderen Prädiktoren haben viel niedrigere PIPs und Koeffizientenschätzungen nahe Null. Unsere BMA-Ergebnisse sind mit dem wahren DGM konsistent.
Speichern wir unsere aktuellen Schätzergebnisse zur späteren Verwendung. Wie bei anderen Bayes’schen Befehlen müssen wir zuerst die Simulationsergebnisse speichern, bevor wir estimates store zum Speichern der Schätzergebnisse verwenden können.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Glaubwürdige Intervalle
bmaregress gibt standardmäßig keine glaubwürdigen Intervalle (CrI) an, da dies eine potenziell zeitaufwändige Simulation der posterioren Stichprobe der Modellparameter erfordert. Wir können sie jedoch nach der Schätzung berechnen.
Wir verwenden zunächst bmacoefsample, um eine MCMC-Stichprobe aus der Posterior-Verteilung der Modellparameter zu erzeugen, die auch die Regressionskoeffizienten enthält. Anschließend verwenden wir den vorhandenen Befehl bayesstats summary, um Posterior-Zusammenfassungen der generierten MCMC-Stichprobe zu berechnen.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
Der 95%-CRI für den Koeffizienten von x2 liegt bei [1,05, 1,34], und der für x10 bei [4,9, 5,26], was mit unserem DGM übereinstimmt.
Beeinflussende Modelle
Die BMA-Koeffizientenschätzungen werden über 1.024 Modelle gemittelt. Es ist wichtig, zu untersuchen, welche Modelle einflussreich sind. Wir können bmastats-Modelle verwenden, um die PMPs zu untersuchen.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Es überrascht nicht, dass das Modell, das sowohl x2 als auch x10 enthält, den höchsten PMP von etwa 63 % aufweist. Tatsächlich entsprechen die beiden besten Modelle einem kumulativen PMP von etwa 77 %:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
Wir können bmagraph pmp verwenden, um die kumulative PMP darzustellen.
. bmagraph pmp, cumulative

Der Befehl stellt standardmäßig die ersten 100 Modelle dar, aber Sie können die Option top() angeben, wenn Sie mehr Modelle sehen möchten.
Wichtige Prädiktoren
Wir können die Bedeutung der Prädiktoren visuell untersuchen, indem wir bmagraph varmap verwenden, um eine Karte mit Variableneinschlüssen zu erstellen.
. bmagraph varmap Computing model probabilities ...

x2 und x10 sind in allen Top-100-Modellen, geordnet nach PMP, enthalten. Ihre Koeffizienten sind in allen Modellen positiv.
Verteilung der Modellgröße
Wir können die Komplexität unseres BMA-Modells erforschen, indem wir bmastats msize und bmagraph msize verwenden, um die Prior- und Posterior-Verteilung der Modellgröße zu untersuchen.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
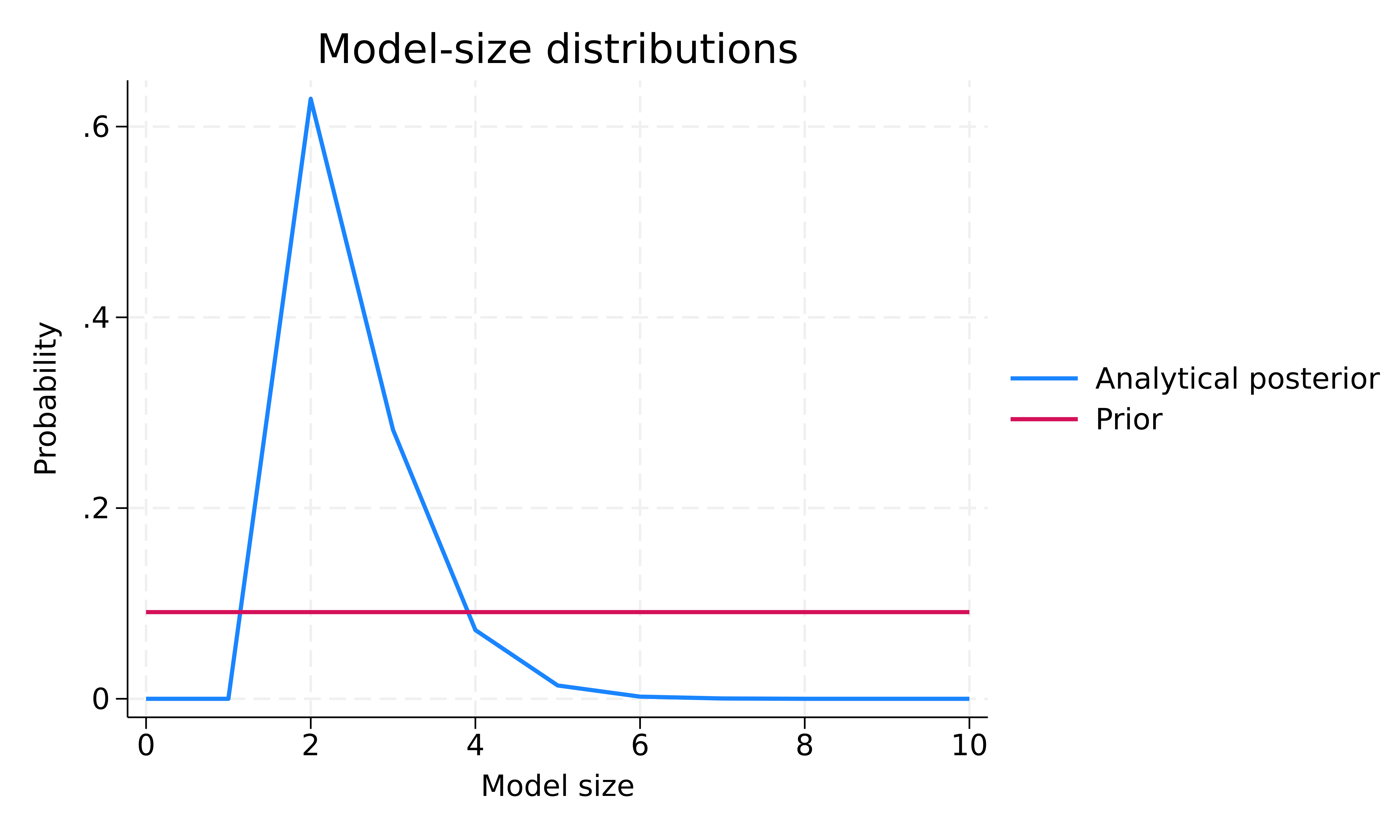
Die vorherige Modellgrößenverteilung ist gleichmäßig über die Modellgröße verteilt. Die posteriore Modellgrößenverteilung ist schief nach links mit einem Modus von etwa 2. Die prioritäre mittlere Modellgröße beträgt 5 und die posteriore 2,48. Auf der Grundlage der beobachteten Daten neigt die BMA also dazu, im Vergleich zu unserer A-priori-Annahme im Durchschnitt kleinere Modelle mit etwa zwei Prädiktoren zu bevorzugen.
Posterior-Verteilung der Koeffizienten
Mit bmagraph coefdensity können wir die Posteriorverteilungen der Regressionskoeffizienten darstellen.
. bmagraph coefdensity {x2} {x3}, combine
Diese Verteilungen sind Mischungen aus einer Punktmasse bei Null, die der Wahrscheinlichkeit der Nichteinbeziehung des Prädiktors entspricht, und einer kontinuierlichen Dichte unter der Bedingung der Einbeziehung. Für den Koeffizienten x2 ist die Wahrscheinlichkeit des Nichteinschlusses vernachlässigbar, so dass seine posteriore Verteilung im Wesentlichen eine kontinuierliche, ziemlich symmetrische Dichte mit dem Mittelpunkt bei 1,2 ist. Für den Koeffizienten x3 gibt es zusätzlich zur bedingten kontinuierlichen Dichte eine rote vertikale Linie bei Null, die der posterioren Nichteinschlusswahrscheinlichkeit von ungefähr 1,2 = 0,8 entspricht.
BMA-Vorhersage
bmapredict erzeugt verschiedene BMA-Vorhersagen. Berechnen wir zum Beispiel die posterioren prädiktiven Mittelwerte.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Wir können auch prädiktive CrIs berechnen, um die Unsicherheit in Bezug auf unsere Vorhersagen zu schätzen. (Dies ist bei vielen traditionellen Modellauswahlmethoden nicht möglich.) Beachten Sie, dass diese prädiktiven CrIs auch die Modellunsicherheit einbeziehen. Um prädiktive CrIs zu berechnen, müssen wir zunächst die posteriore MCMC-Modellparameter-Stichprobe speichern.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Wir fassen die vorhergesagten Ergebnisse zusammen:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Die gemeldeten Durchschnittswerte über die Beobachtungen für die prädiktiven Mittelwerte und die unteren und oberen 95%igen prädiktiven CrI-Grenzen sehen im Verhältnis zu den beobachteten Ergebnissen y vernünftig aus.
Informative Modellprioritäten
Eine der Stärken der BMA ist die Möglichkeit, Vorabinformationen über Modelle und Prädiktoren einzubeziehen. Dies ermöglicht es uns, die Sensitivität der Ergebnisse auf verschiedene Annahmen über die Bedeutung von Modellen und Prädiktoren zu untersuchen. Angenommen, wir haben zuverlässige Informationen darüber, dass alle Prädiktoren außer x2 und x10 mit geringerer Wahrscheinlichkeit mit dem Ergebnis in Zusammenhang stehen. Wir können beispielsweise einen Binomialmodell-Prior mit niedrigen Prior-Einschlusswahrscheinlichkeiten für diese Prädiktoren festlegen.
Um später die Leistung der BMA-Modelle außerhalb der Stichprobe zu vergleichen, teilen wir unsere Stichprobe nach dem Zufallsprinzip in zwei Teile auf und passen das BMA-Modell anhand der ersten Teilstichprobe an. Wir speichern auch die Ergebnisse dieses informativeren BMA-Modells.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Der Effekt dieses Modellpriors ist, dass der PIP aller unwichtigen Prädiktoren nun weniger als 2 % beträgt.
Beachten Sie, dass wir bei der Auswahl eines Modells im Wesentlichen ein BMA-Modell mit einem sehr starken Prior anpassen, der besagt, dass alle ausgewählten Prädiktoren mit einer Wahrscheinlichkeit von 1 enthalten sein müssen. Wir können beispielsweise bmaregress zwingen, alle Variablen in das Modell aufzunehmen:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Vorhersageleistung mit LPS
Zum Vergleich der betrachteten BMA-Modelle wird unser Standard-BMA-Modell unter Verwendung der ersten Teilstichprobe neu berechnet und die Schätzergebnisse gespeichert.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Wir können die Vorhersageleistung unserer BMA-Modelle außerhalb der Stichprobe vergleichen, indem wir bmastats lps verwenden, um den log predictive score (LPS) für Beobachtungen außerhalb der Stichprobe zu berechnen.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Das informativere Modell bmareg_inf hat einen etwas geringeren mittleren LPS, aber die LPS-Zusammenfassungen für alle Modelle sind sehr ähnlich. Siehe [BMA] bmastats lps für den Vergleich der Leistung der BMA-Modelle mit Hilfe von Kreuzvalidierung.
Aufräumen
Während unserer Analyse haben wir mehrere Datensätze erstellt. Wir brauchen sie nicht mehr, also löschen wir sie am Ende. Sie können sie jedoch aufbewahren, vor allem, wenn sie zu einer potenziell zeitaufwändigen Abschlussanalyse gehören.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
