New In 
Байесово осредняване на модела (BMA) за линейна регресия
Защо да избирате само един модел, когато можете да заимствате информация от много други? Новият пакет bma извършва байесовско осредняване на моделите, за да отчете несигурността на моделите във вашия анализ. Не сте сигурни кои предиктори да включите в линейния си регресионен модел? Използвайте bmaregress, за да разберете кои предиктори са важни. Извършване на избор на модел, извод и прогнозиране. Използвайте много команди за последващо оценяване, за да изследвате влиятелни модели, сложност на моделите, пригодност на моделите и ефективност на прогнозиране, анализ на чувствителността към предположенията за важността на моделите и предикторите и др.
Акценти
-
Избор на модел, извод и прогнозиране
-
Изброяване на модели и MC3 извадка
-
Винаги включени и групирани предиктори
-
Приори на модела: равномерни, биномни, бета-биномни
-
Много g-приори, включително хипер-g и стабилни
-
Факторни променливи и оператори за времеви редове
-
Силна, слаба или никаква наследственост за взаимодействията
-
Сходимост на BMA MCMC
-
Постериорни модели и вероятности за включване
-
Предварителни и апостериорни разпределения на размера на модела
-
Постериорни разпределения на параметрите на модела
-
Мерки за съвместност за двойки предиктори
-
Карти на включване на променливи
-
Логистичен прогнозен резултат за пригодност на модела и ефективност на прогнозата
-
Анализ на чувствителността
-
Прогнозиране
-
Поддръжка на стандартни Байесови характеристики след оценяване
-
Вижте още Усредняване на Бейсов модел функции
Въведение
Традиционно избираме един модел и извършваме изводи и прогнози, които зависят от този модел. Нашите резултати обикновено не отчитат несигурността при избора на модел и по този начин могат да бъдат прекалено оптимистични. Те могат дори да бъдат неверни, ако избраният от нас модел се различава съществено от истинския модел, генериращ данни (DGM). В някои приложения може да разполагаме с убедителни теоретични или емпирични доказателства за DGM. В други приложения, обикновено със сложен и нестабилен характер, като тези в икономиката, психологията и епидемиологията, изборът на един надежден модел може да бъде труден.
Вместо да се разчита само на един модел, усредняването на моделите осреднява резултатите от множество правдоподобни модели въз основа на наблюдаваните данни. При БМА „достоверността“ на модела се описва от апостериорната вероятност на модела (АВП), която се определя с помощта на основните Байесови принципи – теоремата на Байес – и се прилага универсално за всички анализи на данни.
BMA може да се използва за отчитане на несигурността на модела при оценяване на параметрите на модела и прогнозиране на нови наблюдения, за да се избегнат прекалено оптимистични заключения. Той е особено полезен в приложения с няколко правдоподобни модела, при които няма една категорична причина да се избере конкретен модел пред останалите. Но дори ако крайната цел е избор на един-единствен модел, BMA може да ви бъде от полза. Той осигурява принципен начин за идентифициране на важни модели и предиктори в рамките на разглежданите класове модели. Нейната рамка ви позволява да научите за взаимовръзките между различните предиктори по отношение на тенденцията им да се появяват в модела заедно, поотделно или независимо. Тя може да се използва за оценка на чувствителността на крайните резултати към различни допускания за важността на различните модели и предиктори. И осигурява оптимални прогнози в смисъл на логаритмичен резултат.
Пакетът bma
В регресионна среда несигурността на модела е свързана с несигурността на това кои предиктори трябва да бъдат включени в модела. Можем да използваме bmaregress, за да отчетем избора на предиктори в линейна регресия. Той изследва пространството на модела или изчерпателно с опцията за изброяване, когато това е възможно, или чрез използване на алгоритъма за съставяне на модели по веригата на Марков Монте Карло (MCMC) (MC3) с опцията за вземане на проби. Той отчита различни обобщения на посетените модели и включените предиктори и на апостериорните разпределения на параметрите на модела. Позволява да се задават групи от предиктори, които да се включват или изключват заедно от даден модел, както и такива, които се включват във всички модели. Той предоставя различни предварителни разпределения за моделите в опцията mprior() и за параметъра g, който контролира свиването на регресионните коефициенти към нула, в опцията gprior(). Поддържа също така факторни променливи и оператори за времеви редове и предоставя няколко начина за обработка на взаимодействията по време на оценяването с помощта на опцията heredity().
Поддържат се много функции за последваща оценка, които включват и някои от стандартните функции за последваща оценка на Бейс.
| Команда | Описание |
|---|---|
|
Постериорни извадки на регресионните коефициенти |
|
|
диаграми модел-вероятност |
|
|
диаграми на разпределение на размера на модела |
|
|
карти за включване на променливи |
|
|
диаграми на постериорната плътност на коефициентите |
|
|
обобщения на задния модел и включването на променливи |
|
|
обобщение на размера на модела |
|
|
апостериорни вероятности за включване (PIP) за предиктори |
|
|
мерки за съгласуваност за предиктори |
|
|
log predictive-score (LPS) |
|
|
Прогнози на BMA |
|
|
Байесови графични обобщения и диагностика на сходимостта |
|
|
Байесова обобщена статистика за параметрите на модела и техните функции |
|
|
Байесови ефективни размери на извадките и свързани статистики |
|
|
Байесови прогнозни р-стойности |
|
|
Прогнози по метода на Бейс |
По-долу ще представим някои характеристики на bma, като използваме набор от данни за играчки. Този набор от данни съдържа n=200�=200 наблюдения, p=10�=10 ортогонални предиктори и резултат y, генериран като
y=0.5+1.2×x2+5×x10+ϵ�=0.5+1.2×�2+5×�10+�
където ϵ∼N(0,1)�∼�(0,1) е стандартен нормален член на грешката.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Изброяване на модели
Използваме bmaregress, за да подготвим линейна регресия BMA на y върху x1 до x10.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
При 10 предиктора и фиксиран (еталонен) g-prior по подразбиране bmaregress използва изброяване на модели и изследва всички 210=1,024210=1,024 възможни модела. Моделът по подразбиране е бета-биномиален с параметри на формата 1, който е еднакъв за размера на модела. A priori нашият модел на BMA предполагаше малко свиване на регресионните коефициенти към нула, тъй като g/(1+g)=0,9950�/(1+�)=0,9950 е близко до 1.
bmaregress идентифицира x2 и x10 като много важни предиктори – техните апостериорни вероятности за включване (PIP) са основно 1. Апостериорните средни оценки на техните регресионни коефициенти са съответно 1,2 (закръглено) и 5,1 и са много близки до истинските стойности 1,2 и 5. Всички други предиктори имат много по-ниски PIP и оценки на коефициентите, близки до нулата. Нашите констатации за BMA са в съответствие с истинската стойност на DGM.
Нека да съхраним настоящите си резултати от оценките за по-късна употреба. Както и при другите Байесови команди, първо трябва да запазим резултатите от симулацията, преди да можем да използваме estimates store (съхраняване на оценки), за да запазим резултатите от оценките.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Достоверни интервали
По подразбиране bmaregress не съобщава достоверни интервали (CrIs), тъй като изисква потенциално отнемаща време симулация на апостериорната извадка от параметри на модела. Но ние можем да ги изчислим след оценяването.
Първо използваме bmacoefsample, за да генерираме MCMC извадка от апостериорното разпределение на параметрите на модела, които включват регресионни коефициенти. След това използваме съществуващата команда bayesstats summary, за да изчислим апостериорните обобщения на генерираната MCMC извадка.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
95% CrI за коефициента x2 е [1,05, 1,34], а този за x10 е [4,9, 5,26], което е в съответствие с нашия DGM.
Влиятелни модели
Оценките на коефициентите на BMA са осреднени за 1024 модела. Важно е да се проучи кои модели са влиятелни. Можем да използваме моделите на bmastats, за да изследваме PMP.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Не е изненадващо, че моделът, който съдържа x2 и x10, има най-висок PMP – около 63%. Всъщност двата най-добри модела отговарят на кумулативен PMP от около 77%:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
Можем да използваме bmagraph pmp, за да изчертаем кумулативния PMP.
. bmagraph pmp, cumulative

Командата изобразява първите 100 модела по подразбиране, но можете да зададете опцията top(), ако искате да видите повече модели.
Важни предиктори
Можем да изследваме важността на предикторите визуално, като използваме bmagraph varmap, за да създадем карта на включените променливи.
. bmagraph varmap Computing model probabilities ...

x2 и x10 са включени във всички 100 топ модела, класирани по PMP. Коефициентите им са положителни във всички модели.
Разпределение на размера на модела
Можем да изследваме сложността на нашия модел на BMA, като използваме bmastats msize и bmagraph msize, за да изследваме предварителното и последващото разпределение на размера на модела.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
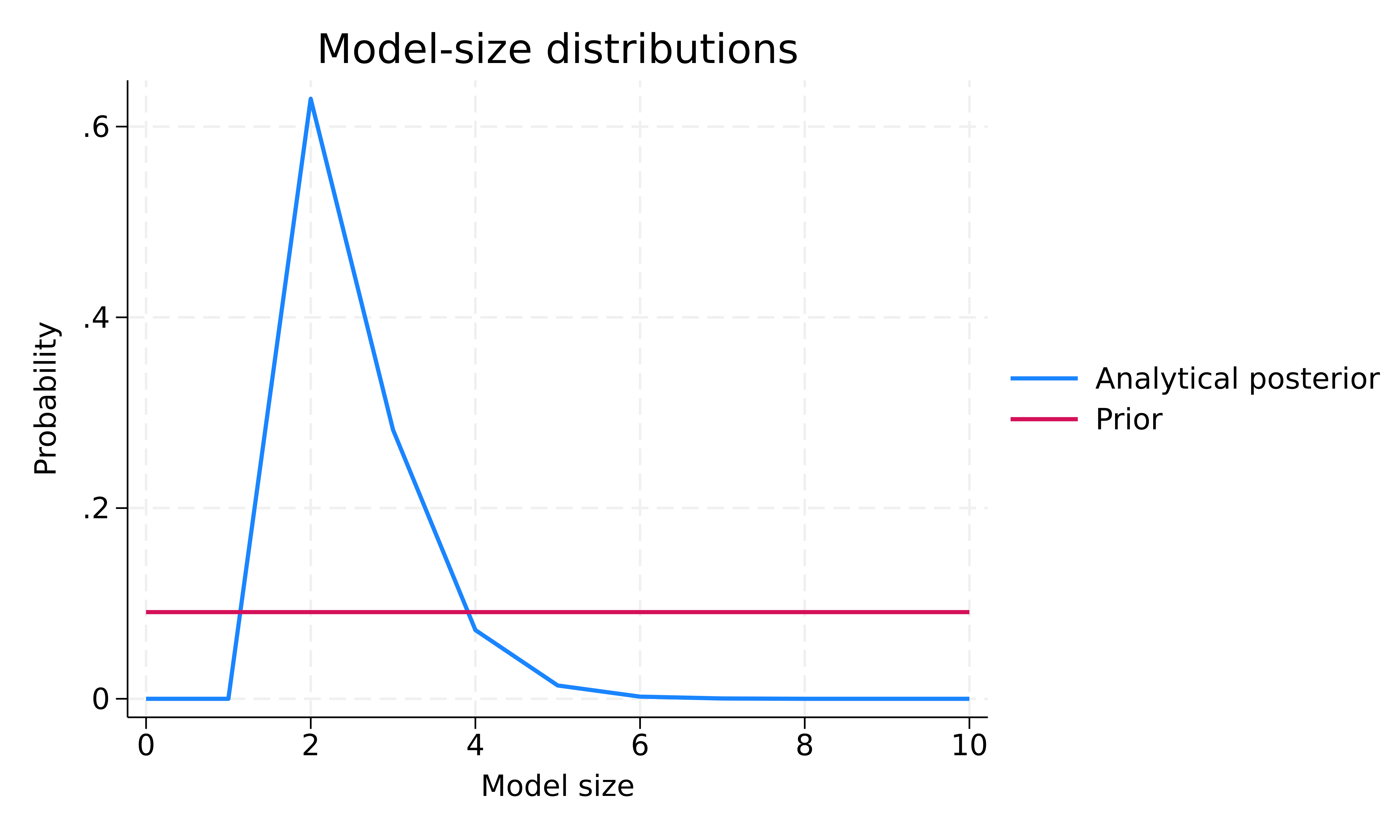
Предварителното разпределение на размера на модела е равномерно за размера на модела. Постериорното разпределение на размера на модела е наклонено наляво с мода около 2. Предварителният среден размер на модела е 5, а постериорният – 2,48. Така че въз основа на наблюдаваните данни BMA има тенденция да предпочита по-малки модели с приблизително два предиктора средно в сравнение с нашето априорно предположение.
Постериорни разпределения на коефициентите
Можем да използваме bmagraph coefdensity, за да изчертаем апостериорните разпределения на регресионните коефициенти.
. bmagraph coefdensity {x2} {x3}, combine
Тези разпределения са смеси от точкова маса в нулата, съответстваща на вероятността за невключване на предсказващия фактор, и непрекъсната плътност, обусловена от включването. За коефициента x2 вероятността за невключване е пренебрежимо малка, така че неговото апостериорно разпределение е по същество непрекъсната, доста симетрична плътност с център 1,2. За коефициента x3, в допълнение към условната непрекъсната плътност, има червена вертикална линия в нулата, съответстваща на апостериорната вероятност за невключване, която е приблизително 1-,2 = 0,8.
Прогноза на BMA
bmapredict изготвя различни прогнози за BMA. Например нека изчислим апостериорните прогнозни средства.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Можем също така да изчислим прогнозни CrI, за да оценим несигурността на нашите прогнози. (Това не е възможно при много от традиционните методи за избор на модел.) Имайте предвид, че тези прогнозни CrI включват и несигурността на модела. За да изчислим прогнозни CrI, първо трябва да запазим апостериорната MCMC извадка от модели и параметри.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Обобщаваме прогнозираните резултати:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Съобщените средни стойности на наблюденията за прогнозните средни стойности и долните и горните 95% прогнозни граници на CrI изглеждат разумни по отношение на наблюдавания резултат y.
Информативни прайори на модела
Една от силните страни на BMA е възможността за включване на предварителна информация за моделите и предикторите. Това ни позволява да изследваме чувствителността на резултатите към различни предположения за важността на моделите и предикторите. Да предположим, че разполагаме с надеждна информация, че всички предиктори, с изключение на x2 и x10, е по-малко вероятно да са свързани с резултата. Можем да зададем например биномна предикация на модел с ниски вероятности за включване на тези предиктори.
За да сравним по-късно представянето на моделите на БМА извън извадката, разделяме извадката си на две части на случаен принцип и прилагаме модела на БМА, като използваме първата подизвадка. Запазваме и резултатите от този по-информативен BMA модел.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Ефектът от този предварителен модел е, че PIP на всички маловажни предиктори вече е по-малък от 2%.
Обърнете внимание, че когато избираме един модел, ние по същество настройваме модел на BMA с много силен приоритет, че всички избрани предиктори трябва да бъдат включени с вероятност 1. Например можем да принудим bmaregress да включи всички променливи в модела:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Прогнозни резултати чрез LPS
За да сравним разглежданите модели на BMA, преизчисляваме нашия модел на BMA по подразбиране, като използваме първата подпроба, и съхраняваме резултатите от оценките.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Можем да сравним прогностичната ефективност на нашите модели на BMA извън извадката, като използваме bmastats lps, за да изчислим логаритмичния прогностичен резултат (LPS) за наблюдения извън извадката.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
По-информативният модел bmareg_inf има малко по-малка средна стойност на LPS, но обобщенията на LPS за всички модели са много сходни. Вижте [BMA] bmastats lps за това как да сравнявате представянето на моделите на BMA, като използвате кръстосано валидиране.
Почистване
По време на нашия анализ генерирахме няколко набора от данни. Вече не се нуждаем от тях, затова ги изтриваме накрая. Но вие може да решите да ги запазите, особено ако те съответстват на потенциално отнемащ време финален анализ.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
