Az egyenletek két értelemben lehetnek dinamikusak: a késések a visszafelé néző viselkedést, míg a várható jövőbeli értékek a jövőbe mutató magatartást rögzítik. A DSGE-modellek felhasználhatók olyan politikák elemzésére, mint a monetáris sokkok, a fiskális sokkok stb.
A Bayes-i becslés két lépésből áll: meghatározzuk a DSGE modellt és meghatározzuk a DSGE modell paramétereinek prioritásait.
Egy kis New Keynes-i modell rendelkezik egy befektetés-megtakarítási (IS) egyenlettel, amely összeköti a kibocsátási rést a kamatlábbal, egy Phillips-görbével, amely az inflációt a kibocsátási réshez kapcsolja, és egy Taylor-szabályt, amely a kamatlábat az inflációhoz köti.
A Stata szintaxisában a modell így néz ki:

    (   x = F.x - (r - F.p - z)   , unobserved ) ///
    (   p = {beta}*F.p + {kappa}*x             ) ///
    (   r = 1/{delta}*p + m                    ) ///
    ( F.z = {rhoz}*z, state                    ) ///
    ( F.m = {rhom}*m, state                    )

Az első egyenlet egy IS görbe, a második egy Phillips görbe, a harmadik pedig egy Taylor-szabály. A negyedik egyenlet IS-sokk, az ötödik egyenlet pedig a Taylor-szabály monetáris sokkja. Az IS görbe unobserved t opciója azt jelzi, hogy a kimeneti rést nem megfigyeltként kezeljük.
Minden paraméterhez hozzáadunk egy előzetes specifikációt. Számos DSGE paraméternek van olyan értelmezése, amely természetesen korlátozza az elfogadható értékek tartományát. A Phillips görbe {beta} paramétere diszkontráta, amelynek 0 és 1 között kell lennie. A {kappa} paraméter egy árkiigazítási paraméter, amelyet gyakran kicsinek, de pozitívnak tartanak. A {delta} paraméter a Taylor-szabály inflációs kiigazítási együtthatójának inverze, tehát 0 és 1 között kell lennie. Ezen tartomány-korlátozások mellett lehet, hogy a paraméterérték valószínű helyére vonatkozóan elsőbbséget kell megadni. A diszkontráta valószínűleg 0,95 körül van, az inflációs kiigazítási paraméter 0,2 körül, az inverz inflációs kiigazítási együttható pedig 0,66 körül (1,5 Taylor-szabály-együttható esetén). A Priors lehetővé teszi, hogy ezt az információt kifejezetten beépítse a becslésbe.
Vegyük figyelembe az inflációs ráta és a szövetségi alapok arányát 1955 óta.

. webuse usmacro2
(Federal Reserve Economic Data - St. Louis Fed, 2017-01-15)

. describe p r


Variable     Storage     Display     Value                          
    name        type      format     label    Variable label        

  p            double     %10.0g              Growth rate of prices (GDPDEF)
  r            double     %10.0g              Federal funds rate (FEDFUNDS)
         
  

. summarize p r


         
 
                                                     
 Variable
 
         Obs         Mean       Std. dev.        Min        Max

       p 
 
        2.44     3.236709       2.281433   -.6681431   11.60957
       r 
 
        2.44     5.035328        3.59569         .07       19.1

Gathering up both the prior specification and the model specification, our estimation command is

. bayes, prior({beta},  beta(95,5))                   ///
         prior({kappa}, beta(30,70))                  ///
         prior({delta}, beta(60,30))                  ///
         prior({rhoz},  beta(10,10))                 ///
         prior({rhom},  beta(10,10))                 ///
         rseed(17) :                                  ///
         dsge (  x = F.x - (r - F.p - z), unobserved) ///
              (  p = {beta}*F.p + {kappa}*x         ) ///
              (  r = 1/{delta}*p + m                ) ///
              (F.z = {rhoz}*z, state                ) ///
              (F.m = {rhom}*m, state                )
note: initial parameter vector set to means of priors.

Burn-in ...
Simulation ...

Model summary
Likelihood:
  p r ~ dsgell({beta},{kappa},{delta},{rhoz},{rhom},{sd(e.z)},{sd(e.m)})

Priors:
             {beta} ~ beta(95,5)
            {kappa} ~ beta(30,70)
            {delta} ~ beta(60,30)
        {rhoz rhom} ~ beta(10,10)
  {sd(e.z) sd(e.m)} ~ igamma(.01,.01)

Bayesian linear DSGE model                     MCMC iterations  =     12,500
Random-walk Metropolis–Hastings sampling       Burn-in          =      2,500
                                               MCMC sample size =     10,000
Sample: 1955q1 thru 2015q4                     Number of obs    =        244
                                               Acceptance rate  =      .2483
                                               Efficiency:  min =    .005767
                                                            avg =     .02115
Log marginal-likelihood = -794.29162                        max =     .03808



       
 
                                                               
       
 
                                                     Equal-tailed
       
 
     Mean     Std. dev.      MCSE     Median     [95% cred. interval]

      beta
 
 .9406005     .0243801    .001984   .9428465     .8869374   .9812481
     kappa
 
  .206337     .0327608    .001679   .2046031     .1470858    .273637
     delta
 
 .5832685     .0404188    .004897   .5835278      .497712   .6607058
      rhoz
 
 .9171911      .015764    .000978   .9170596     .8846393   .9467265
      rhom
 
  .561412     .0296339    .001667   .5621747     .5036024   .6184265
    sd(e.z)
 
 .5280986      .057275    .003639   .5255331     .4217194   .6467684
    sd(e.m)
 
 2.161816     .1585077    .020872   2.141682     1.902066   2.533669

A modell összefoglaló bemutatja a valószínűség modellt és az előzetes specifikációkat. A standard eltérések kivételével mindenkinek meg kell adnia a priorokat. A DSGE modellek esetében ennek van értelme, mert a paraméterek összefüggenek a gazdaságelmélettel. Például a {beta} diszkont faktor tényezője a béta, 95 és 5 alakparaméterekkel. A sokkok átlagos eltéréseit a z és m állapotváltozókhoz alapértelmezett inverz gamma priorokhoz rendeltük
A becslés kimenete megjeleníti a beégési periódusok számát (2500), az MCMC mintaméretét (10 000), az adatok mintaméretét (244 periódus), a mintavételi periódust (1955q1 – 2015q4), valamint a a becslés folyamata. Az elfogadási arány az elfogadott MCMC húzások töredékére vonatkozik. Az alkalmazott Metropolis – Hastings mintavevő tipikus értékei 20-30%; elfogadási arányunk 24%. A hatékonyság az MCMC rajzok autokorrelációjával függ össze, és jelzi, hogy a mintavevő milyen gyorsan haladja át a paraméterteret. Átlagos hatékonyságunk 2,1%.
A becslés kimenete a utólagos paraméterek átlagát, a szórásokat, a mediánokat és az egyenlő farokú hiteles intervallumokat mutatja. A {beta} hátsó átlaga 0,94, nagyon közel a korábbi 0,95-ös átlaghoz. A {kappa} hátsó átlaga körülbelül 0,21, alacsonyabb, mint a korábbi 0,30. A {delta} hátsó átlaga 0,58, alacsonyabb, mint a korábbi 0,66 átlag. Mindkét sokk nagyon perzisztens, a posterior átlagos autokorrelációs együtthatók z-n és m-n 0,92, illetve 0,56. A sokkok standard eltéréseinek hátsó középértéke 0,53 az IS sokk esetében z, és 2,16 a Taylor-szabály monetáris sokkja esetén m.
A Stata összes Bayes-féle utóértékelési funkciója bayes: dsge után működik.
Ábrázolhatjuk az előzetes beállítási paraméter {kappa} hátsó sűrűségét.

. bayesgraph kdensity {kappa}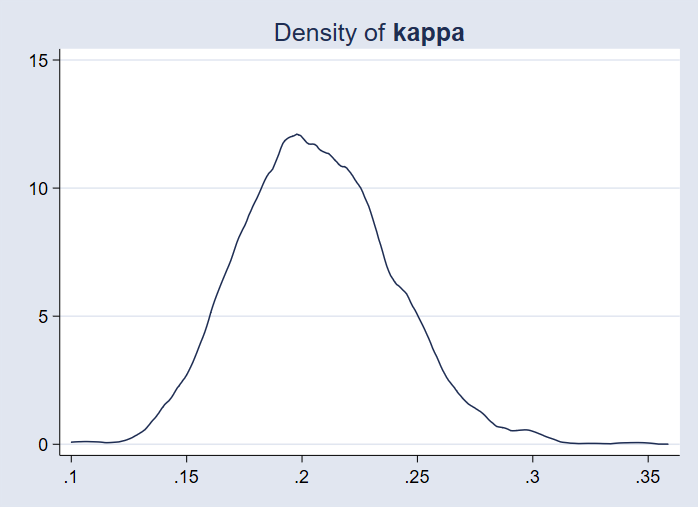

Megtervezhetjük a {kappa} teljes diagnosztikai készletét.

. bayesgraph diagnostics {kappa}

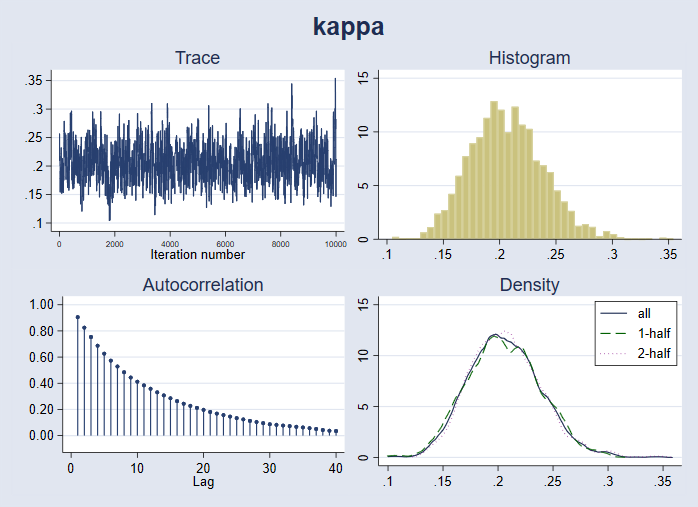
Hozzáadhatjuk az előzetes sűrűséget a hátsó sűrűség diagramhoz, hogy vizuálisan összehasonlítsuk az előtti és a hátsó sávot.

. bayesgraph kdensity kappa, addplot(function Prior = betaden(30,70,x), ///
         legend(on label(1 "Posterior")) lcolor(blue))

Megvizsgálhatjuk a modell paramétereinek függvényeinek hátsó sűrűségét, például a Taylor-szabály együtthatóját 1/{delta}.

. bayesstats summary (1/{delta})

Posterior summary statistics                       MCMC sample size =      10,000

        expr1 : 1/delta



       
 
                                                               
       
 
                                                     Equal-tailed
       
 
     Mean     Std. dev.      MCSE     Median     [95% cred. interval]

      expr1
 
 1.722922     .1225577    .015302   1.713714      1.513533   2.009195

Az 1/{delta} utólagos átlaga 1,7, magasabb, mint a korábbi 1,5-es átlag, és jelzi a kamatlábak erős válaszát az infláció változásaira.
Kiszámíthatjuk a Bayes-impulzus-válasz függvényeket. Először elmentjük az MCMC eredményeit az nk_mcmc.dta adatkészletbe. Ezt megtehetjük becslés közben a saving() opcióval, vagy becslés után is úgy, hogy a bayes parancsot visszajátszjuk a saving() opcióval.

. bayes, saving(nk_mcmc.dta, replace)
note: file nk_mcmc.dta not found; file saved.

A mentett MCMC mintával impulzus-válasz funkciókat készíthetünk a bayesirf csomaggal. Ez a parancssor kiterjeszti az irf-t a bayesi becslés befogadására, és a Ez a parancssor kiterjeszti az irf-t a bayesi becslés befogadására, és a bayes: dsge, bayes: dsgenl, és bayes: var után érhető el.
(file bayes_irfs.irf created)
(file bayes_irfs.irf now active)

. bayesirf create nk_model
(file bayes_irfs.irf updated)

. bayesirf graph irf, impulse(m) response(x p r m)

A bal felső panel mutatja az m monetáris állapot változó válaszát önmagára adott sokkra. A jobb felső panel mutatja az infláció reakcióját a sokkra: csökken, majd monoton visszatér az egyensúlyi állapotba. A bal alsó panelen látható a kamatláb válasza: emelkedik. Végül a jobb alsó panel mutatja a kimeneti rés válaszát: 0 alá esik, recessziót jelezve. A kontrakciós monetáris sokk emeli tehát a kamatlábat, csökkenti az inflációt és a kibocsátás csökkenését okozza.
Mindez és még sok más elvégezhető a bayes: dsge paranccsal.

Nemlineáris DSGE modell

A bayes előtag a dsgenl paranccsal is működik, amely elsőrendű zavarral becsüli meg a nemlineáris DSGE modellek paramétereit.
Ezután megbecsüljük a sztochasztikus növekedési modell paramétereit. A modell a fogyasztás, a reálkamat, a GDP, a tőkeállomány és a termelékenység egyenleteit tartalmazza.

 (1/c     = {beta}*(1/F.c)*(1+F.r-{delta})    )       ///
 (r       = {alpha}*y/k                       )       ///
 (y       = z*k^({alpha})                     )       ///
 (f.k     = y - c + (1-{delta})*k             )       ///
 (ln(f.z) = {rho}*ln(z)                       ) ,     ///
 exostate(z) endostate(k) observed(y) unobserved(c r)

A makroökonómusok ezeket az összefüggéseket fogyasztási Euler-egyenletként, tőkekövetelmény-egyenletként, termelési függvényként, tőkefelhalmozási egyenletként és a termelékenység mozgási törvényeként fogják felismerni.
A paraméterek értelmezése: a {beta} a diszkontráta, amelyet általában úgy gondolnak, hogy körülbelül 0,95;az {alpha} a tőke jövedelemaránya, általában úgy gondolják, hogy körülbelül egyharmada;a {delta} az amortizációs ráta, általában negyedévente 2,5%;az {rho} pedig a technológiai sokk fennmaradása. A Priorokat arra használják, hogy ezt az információt a becsléshez igazítsák.
Becsüljük meg ennek a modellnek a paramétereit kicsinyített kimenet segítségével. Az m1gdp.dta adatkészlet biztosítja a kimenet logaritmusát.

. webuse m1gdp, clear

. describe

Contains data from  https://www.stata-press.com/data/r17/m1gdp.dta
 Observations:            223
    Variables:              3                   26 Mar 2020 02:49


Variable     Storage     Display     Value                          
    name        type      format     label    Variable label        

  t               int        %tq              Quarterly time variable
  ln_m1         float      %9.0g              ln(M1) monthly to quarterly by
                                               averaging: M1 is Fred M1SL, Bil
                                               of $ seas adj
  ln_gdp        float      %9.0g              ln(gdpc1) FRED GDP in Bil of 1996
                                               chained $ seas adj

Sorted by: t

A tsfilter parancs kivonja a kimenet trendkomponensét. Hodrick – Prescott szűrőt használunk, majd 100-szorosára növeljük az eredményt. A kapott skála olyan, hogy 1-es érték azt jelzi, hogy a GDP 1% -kal haladja meg a trendértékét.

. tsfilter hp y = ln_gdp

. replace y = 100*y
(222 real changes made)

. tsline y, title("HP-detrended output")

A recesszió a kibocsátás trend alatti csökkenésével, míg a fellendülés a kibocsátás trend feletti emelkedésével jár.
Folytatjuk a paraméterek becslését.

. bayes, prior({alpha}, beta(30,70))                ///
         prior({beta},  beta(95,5))                 ///
         prior({delta}, beta(25,900))               ///
         prior({rho},   beta(10, 10))               ///
         rseed(20) dots saving(rbc_mcmc, replace):  ///
         dsgenl (1/c      = {beta}*(1/F.c)*(1+f.r-{delta})    )       ///
                 (r       = {alpha}*y/k                       )       ///
                 (y       = z*k^({alpha})                     )       ///
                 (f.k     = y - c + (1-{delta})*k             )       ///
                 (ln(f.z) = {rho}*ln(z)                       ) ,     ///
                 exostate(z) endostate(k) observed(y) unobserved(c r)
note: initial parameter vector set to means of priors.

Burn-in 2500 aaaaaaaaa1000aaaaaa...2000..... done
Simulation 10000 .........1000.........2000.........3000.........4000.........
5000.........6000.........7000.........8000.........9000.........10000 done

Model summary
Likelihood:
  y ~ dsgell({beta},{delta},{alpha},{rho},{sd(e.z)})

Priors:
     {beta} ~ beta(95,5)
    {delta} ~ beta(25,900)
    {alpha} ~ beta(30,70)
      {rho} ~ beta(10,10)
  {sd(e.z)} ~ igamma(.01,.01)
Bayesian first-order DSGE model                  MCMC iterations  =     12,500
Random-walk Metropolis–Hastings sampling         Burn-in          =      2,500
                                                 MCMC sample size =     10,000
Sample: 1947q1 thru 2002q2                       Number of obs    =        222
                                                 Acceptance rate  =      .2189
                                                 Efficiency:  min =     .02528
                                                              avg =     .04236
Log marginal-likelihood =  -311.7914                          max =     .05567



       
 
                                                               
       
 
                                                   Equal-tailed
       
 
     Mean     Std. dev.      MCSE     Median   [95% cred. interval]

      beta
 
 .9095501     .0392698    .001886   .9133171   .8231531   .9726171
     delta
 
 .0286052     .0054865    .000345      .0284   .0192159   .0404854
     alpha
 
 .2768864     .0451422    .002097   .2738962   .1964999   .3772306
       rho
 
 .7680742      .036755    .001813   .7680699   .6950177   .8412948
    sd(e.z)
 
 .9340691     .0458306    .001943   .9328126   .8502487   1.032548

A {béta} diszkontráta korábbi átlaga 0,95; hátsó átlaga alig változott 0,91-nél. Az amortizációs ráta (delta) korábbi átlaga 0,025; hátsó átlaga alig változott 0,0286-nál. Az aa korábbi átlaga 0,3; hátsó átlaga valamivel alacsonyabb, 0,28.
Eközben az {rho} hátsó átlaga 0,77, sokkal nagyobb, mint korábbi, 0,5-es átlaga. A technológiai sokk szórása körülbelül 1.
Ezután az impulzus-válasz funkciókat egy technológiai sokkhoz számítjuk.

. bayesirf set bayes_irf2.irf, replace
(file bayes_irf2.irf created)
(file bayes_irf2.irf now active)

. bayesirf create rbc_model, step(16)
(file bayes_irf2.irf updated)

. bayesirf graph irf, impulse(z) byopts(yrescale)

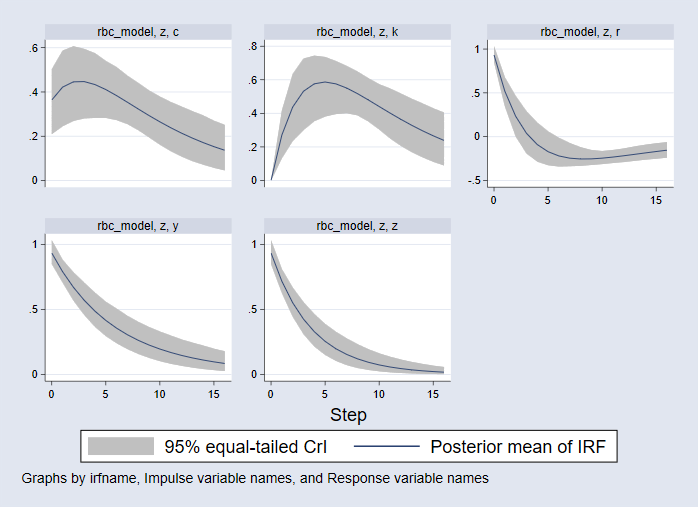
A függőleges tengely egységei százalékos eltérésekben vannak az állandótól. A vízszintes tengely egységei ugyanabban az időtartamban vannak, mint az adatok, vagyis a negyedek. 16 lépés (4 év) választ adunk meg.

• A fogyasztási választ a bal felső panelen ábrázoljuk. A fogyasztás az ütközéskor növekszik, majd púp alakú mintázatban tovább növekszik, mielőtt visszaállna állandósult állapotába.
• A tőkeállomány válaszát a felső-középső panel ábrázolja. A tőkeállomány nem változik hatással, de később 0,6% -os csúcsra emelkedik az egyensúlyi állapota fölött, mielőtt csökken.
• A jobb felső sarokban a kamatláb a hatás hatására emelkedik, majd csökken; négy negyed után 0 alá süllyed, majd alulról visszatér állandósult állapotába.
• A bal alsó panel ábrázolja a kimenet válaszát; becsapódáskor felemelkedik, majd monoton módon visszaáll állandó állapotába.
• Az alsó-középső panel maga a technológia reakcióját ábrázolja. Ez is emelkedik az ütközéskor, majd monoton módon visszaáll az egyensúlyi állapotába.

A pontos hátsó eszközöket és a hiteles intervallumokat a bayesirf táblázattal lehet megtekinteni. Az alábbiakban összefoglaljuk a fogyasztás reakcióját a technológiai sokkra.

. bayesirf table irf, impulse(z) response(c)

Results from rbc_model



       
 
                                  
       
 
     (1)        (2)         (3)   
  step 
 
     irf       Lower       Upper  

      0
 
 .363699     .209593     .502829
      1
 
 .421867     .245335     .587063
      2
 
 .445802     .269215     .606835
      3
 
 .446962     .280481     .595064
      4
 
 .433453     .282893     .575041
      5
 
 .410962     .282863     .540024
      6
 
 .383436     .272859     .511974
      7
 
 .353574     .254899     .473345
      8
 
 .323189     .227486     .440766
      9
 
 .293459     .195011      .40683
     10
 
 .265119     .162333     .379442
     11
 
 .238595     .133143     .354938
     12
 
 .214099     .108564     .334151
     13
 
   .1917     .087822     .313609
     14
 
 .171372     .071785     .294301
     15
 
 .153031     .057275     .270277
     16
 
 .136556     .045631     .251522

Posterior means reported
95% equal-tailed credible lower and upper bounds reported.
(1) irfname = rbc_model, impulse, = z, and response = c.

Az egy standard eltérésű technológiai sokk után a fogyasztás a sokkot követő harmadik időszakban 0,477% -kal emelkedik az egyensúlyi állapota fölé.