Neu in 
Bayessche lineare und nichtlineare DSGE-Modelle
Das Bayes-Präfix unterstützt nun die Befehle dsge und dsgenl zur Anpassung von linearen und nichtlinearen dynamischen stochastischen allgemeinen Gleichgewichtsmodellen (DSGE) nach Bayes.
DSGE-Modelle sind in der Makroökonomie und im Finanzwesen beliebt, um mehrere Zeitreihen zu modellieren. Die Modelle enthalten Systeme von linearen oder nichtlinearen Gleichungen, die verschiedene wirtschaftliche Prozesse beschreiben. Die Parameter von DSGE-Modellen haben typischerweise eine direkte Interpretation im Kontext der Wirtschaftstheorie und haben oft festgelegte Bereiche plausibler Werte. Diese Bereiche (oder Beschränkungen) sollten in die Schätzung einbezogen werden, um stabile Ergebnisse zu erhalten.
Die Bayes’sche Schätzung bietet eine natürliche Möglichkeit, solche Einschränkungen zu berücksichtigen, indem verschiedene Priorverteilungen für Modellparameter spezifiziert werden, die die Einschränkungen erfüllen.
Zeigen Sie, wie es funktioniert
Lineares DSGE-Modell
Ein DSGE-Modell besteht aus einem System von Gleichungen, die wirtschaftliche Variablen wie Inflation, Zinssatz und Produktionslücke miteinander und mit exogenen Zustandsvariablen, die das System antreiben, in Beziehung setzen.
Highlights
- Bayessche dynamische stochastische allgemeine Gleichgewichtsmodelle
- Lineare und nichtlineare Modelle
- Standard- und benutzerdefinierte Prioritäten
- Flexible Steuerung des MCMC-Samplings
- Bayessche zusammenfassende Statistik
- MCMC-Diagnosen
- Mehrere Ketten
- Impuls-Antwort-Funktionen
- Graphen und Tabellen von IRFs
- Speichern und Vergleichen von Modellen
- Volle Unterstützung von Bayes’schen Postestimationsfunktionen
Gleichungen können in zweierlei Hinsicht dynamisch sein: Verzögerungen erfassen rückwärtsgerichtetes Verhalten, während erwartete zukünftige Werte zukunftsgerichtetes Verhalten erfassen. DSGE-Modelle können verwendet werden, um politische Maßnahmen zu analysieren, z. B. die Auswirkungen von monetären Schocks, fiskalischen Schocks usw.
Die Bayes’sche Schätzung besteht aus zwei Schritten: Spezifizierung des DSGE-Modells und Spezifizierung der Prioritäten für die DSGE-Modellparameter.
Ein kleines neukeynesianisches Modell hat eine Investitions-Spar-Gleichung (IS), die die Produktionslücke mit dem Zinssatz verbindet, eine Phillips-Kurve, die die Inflation mit der Produktionslücke verbindet, und eine Taylor-Regel, die den Zinssatz mit der Inflation verbindet. In der Stata-Syntax sieht das Modell wie folgt aus:
( x = F.x - (r - F.p - z) , unobserved ) ///
( p = {beta}*F.p + {kappa}*x ) ///
( r = 1/{delta}*p + m ) ///
( F.z = {rhoz}*z, state ) ///
( F.m = {rhom}*m, state )
Die erste Gleichung ist eine IS-Kurve, die zweite ist eine Phillips-Kurve und die dritte ist eine Taylor-Regel. Die vierte Gleichung ist ein IS-Schock, und die fünfte Gleichung ist ein monetärer Schock nach der Taylor-Regel.
Die unbeobachtete Option in der IS-Kurve zeigt an, dass wir die Produktionslücke als unbeobachtet behandeln. Wir passen das Modell an die Daten zur Inflation und zum Zinssatz an.
Wir fügen eine Prior-Spezifikation für jeden Parameter hinzu. Viele DSGE-Parameter haben Interpretationen, die den Bereich der zulässigen Werte natürlich einschränken. Der Parameter {beta} in der Phillips-Kurve ist ein Diskontsatz und muss zwischen 0 und 1 liegen. Der Parameter {kappa} ist ein Preisanpassungsparameter, von dem oft angenommen wird, dass er klein aber positiv ist. Der Parameter {delta} ist die Umkehrung des Inflationsanpassungskoeffizienten der Taylor-Regel und muss daher zwischen 0 und 1 liegen. Zusätzlich zu diesen Bereichsrestriktionen könnte man Vorannahmen über die wahrscheinliche Lage des Parameterwertes haben. Der Diskontsatz liegt wahrscheinlich um 0,95, der Inflationsanpassungsparameter um 0,2 und der inverse Inflationsanpassungskoeffizient um 0,66 (für einen Taylor-Regel-Koeffizienten von 1,5). Mit Prioren können Sie diese Informationen explizit in die Schätzung einbeziehen.
Betrachten Sie die Daten zur Inflationsrate und zur Federal Funds Rate seit 1955.
. webuse usmacro2 (Federal Reserve Economic Data - St. Louis Fed, 2017-01-15) . describe p r
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| p double %10.0g Growth rate of prices (GDPDEF) | ||
| r double %10.0g Federal funds rate (FEDFUNDS) | ||
| Variable | Obs Mean Std. dev. Min Max | |
| p | 2.44 3.236709 2.281433 -.6681431 11.60957 | |
| r | 2.44 5.035328 3.59569 .07 19.1 |
Gathering up both the prior specification and the model specification, our estimation command is
. bayes, prior({beta}, beta(95,5)) ///
prior({kappa}, beta(30,70)) ///
prior({delta}, beta(60,30)) ///
prior({rhoz}, beta(10,10)) ///
prior({rhom}, beta(10,10)) ///
rseed(17) : ///
dsge ( x = F.x - (r - F.p - z), unobserved) ///
( p = {beta}*F.p + {kappa}*x ) ///
( r = 1/{delta}*p + m ) ///
(F.z = {rhoz}*z, state ) ///
(F.m = {rhom}*m, state )
note: initial parameter vector set to means of priors.
Burn-in ...
Simulation ...
Model summary
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| beta | .9406005 .0243801 .001984 .9428465 .8869374 .9812481 | |
| kappa | .206337 .0327608 .001679 .2046031 .1470858 .273637 | |
| delta | .5832685 .0404188 .004897 .5835278 .497712 .6607058 | |
| rhoz | .9171911 .015764 .000978 .9170596 .8846393 .9467265 | |
| rhom | .561412 .0296339 .001667 .5621747 .5036024 .6184265 | |
| sd(e.z) | .5280986 .057275 .003639 .5255331 .4217194 .6467684 | |
| sd(e.m) | 2.161816 .1585077 .020872 2.141682 1.902066 2.533669 | |
Die Modellzusammenfassung zeigt das Wahrscheinlichkeitsmodell und die Prior-Spezifikationen. Die Prioren für alle außer den Standardabweichungen sind erforderlich. Im Falle von DSGE-Modellen ist dies sinnvoll, weil die Parameter mit der ökonomischen Theorie zusammenhängen. Zum Beispiel ist der Prior für den Diskontierungsfaktor {beta} beta mit den Formparametern 95 und 5. Den Standardabweichungen der Schocks auf die Zustandsvariablen z und m wurden standardmäßige inverse Gamma-Prioren zugewiesen.
Die Ausgabe der Schätzung zeigt die Anzahl der Burn-In-Perioden (2.500), den MCMC-Stichprobenumfang (10.000), den Stichprobenumfang der Daten (244 Perioden), den Stichprobenzeitraum (1955q1 bis 2015q4) sowie die Akzeptanzrate und die Effizienz des Schätzprozesses. Die Akzeptanzrate bezieht sich auf den Anteil der MCMC-Ziehungen, der akzeptiert wurde. Typische Werte für den verwendeten Metropolis-Hastings-Sampler sind 20% bis 30%; unsere Akzeptanzrate ist 24%. Die Effizienz bezieht sich auf die Autokorrelation der MCMC-Ziehungen und gibt an, wie schnell der Sampler den Parameterraum durchläuft. Unsere durchschnittliche Effizienz beträgt 2,1 %.
Die Ausgabe der Schätzung zeigt die Posterior-Parameter-Mittelwerte, Standardabweichungen, Mediane und gleichschenklige Glaubwürdigkeitsintervalle an. Der Posterior-Mittelwert von {beta} ist 0,94, was sehr nahe an seinem Prior-Mittelwert von 0,95 liegt. Der posteriore Mittelwert von {kappa} ist etwa 0,21, niedriger als der vorherige Mittelwert von 0,30. Der posteriore Mittelwert für {delta} ist 0,58, niedriger als der vorherige Mittelwert von 0,66. Beide Schocks sind sehr persistent, mit posterioren mittleren Autokorrelationskoeffizienten für z und m von 0,92 bzw. 0,56. Die posterioren Mittelwerte der Standardabweichungen der Schocks sind 0,53 für den IS-Schock z und 2,16 für den Taylor-Regel-Geldschock m.
Alle Bayes’schen Postestimationsfunktionen von Stata funktionieren nach bayes: dsge.
Wir können die Posterior-Dichte des Prior-Anpassungsparameters {kappa} darstellen.
. bayesgraph kdensity {kappa}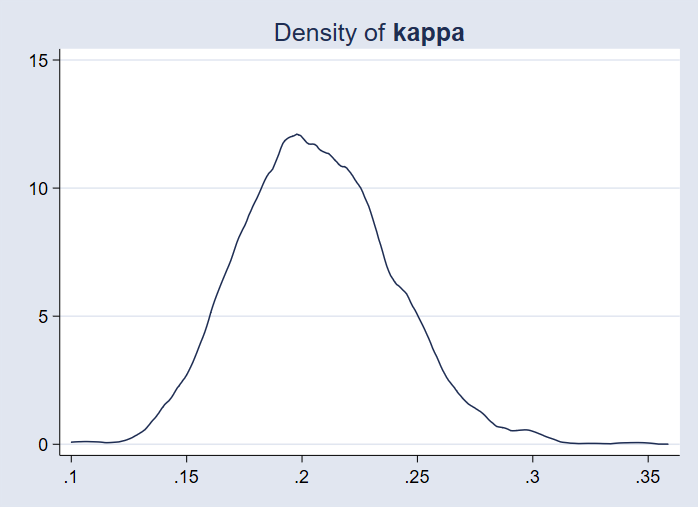
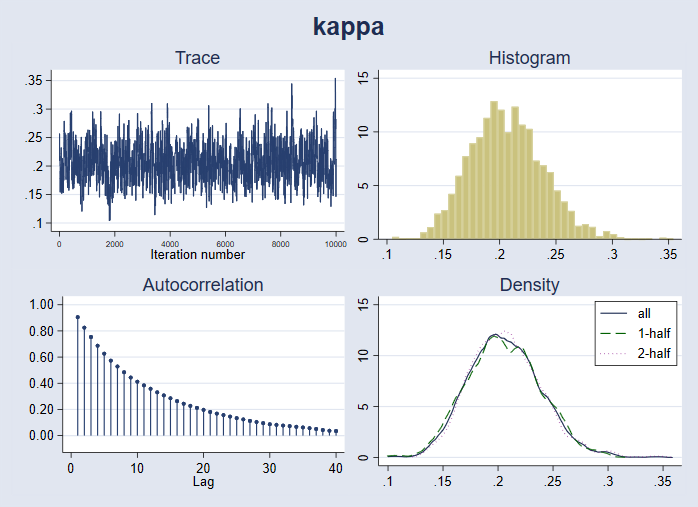
Wir können einen vollständigen Satz von Diagnosen für {kappa} darstellen.
. bayesgraph diagnostics {kappa}
Wir können die Prior-Dichte zum Posterior-Dichte-Diagramm hinzufügen, um Prior und Posterior visuell zu vergleichen.
. bayesgraph kdensity kappa, addplot(function Prior = betaden(30,70,x), ///
legend(on label(1 "Posterior")) lcolor(blue))

Wir können die Posterior-Dichten von Funktionen der Modellparameter untersuchen, wie z. B. den Taylor-Regel-Koeffizienten 1/{delta}.
. bayesstats summary (1/{delta})
Posterior summary statistics MCMC sample size = 10,000
expr1 : 1/delta
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| expr1 | 1.722922 .1225577 .015302 1.713714 1.513533 2.009195 | |
Der posteriore Mittelwert für 1/{delta} ist 1,7, höher als der vorherige Mittelwert von 1,5 und deutet auf eine starke Reaktion der Zinssätze auf Änderungen der Inflation hin.
Wir können Bayes’sche Impuls-Antwort-Funktionen berechnen. Zuerst speichern wir die MCMC-Ergebnisse in einem Datensatz, nk_mcmc.dta. Wir können dies während der Schätzung mit der Option saving() tun oder auch nach der Schätzung, indem wir den Bayes-Befehl mit der Option saving() erneut abspielen.
. bayes, saving(nk_mcmc.dta, replace) note: file nk_mcmc.dta not found; file saved.
Wenn die MCMC-Stichprobe gespeichert ist, können wir mit der bayesirf-Suite Impuls-Antwort-Funktionen konstruieren. Diese Befehlssuite erweitert irf für die Bayes’sche Schätzung und ist nach bayes: dsge, bayes: dsgenl und bayes: var verfügbar.
. bayesirf set bayes_irfs.irf, replace (file bayes_irfs.irf created) (file bayes_irfs.irf now active) . bayesirf create nk_model (file bayes_irfs.irf updated) . bayesirf graph irf, impulse(m) response(x p r m)

Das linke obere Feld zeigt die Reaktion der monetären Zustandsvariablen m auf einen Schock an sich selbst. Das rechte obere Feld zeigt die Reaktion der Inflation auf den Schock: Sie sinkt und kehrt dann monoton zum Steady-State zurück. Das untere linke Feld zeigt die Reaktion des Zinssatzes: er steigt. Das untere rechte Feld schließlich zeigt die Reaktion der Produktionslücke: Sie fällt unter 0, was auf eine Rezession hindeutet. Der kontraktive monetäre Schock erhöht also den Zinssatz, reduziert die Inflation und bewirkt einen Rückgang der Produktion.
All dies und mehr kann mit dem Befehl bayes: dsge durchgeführt werden.
Nichtlineares DSGE-Modell
Das Bajes-Präfix funktioniert auch mit dem Befehl dsgenl, der die Parameter nichtlinearer DSGE-Modelle durch eine Störung erster Ordnung schätzt.
Als nächstes schätzen wir die Parameter eines stochastischen Wachstumsmodells. Das Modell hat Gleichungen für den Konsum, den realen Zinssatz, das BIP, den Kapitalstock und die Produktivität.
(1/c = {beta}*(1/F.c)*(1+F.r-{delta}) ) ///
(r = {alpha}*y/k ) ///
(y = z*k^({alpha}) ) ///
(f.k = y - c + (1-{delta})*k ) ///
(ln(f.z) = {rho}*ln(z) ) , ///
exostate(z) endostate(k) observed(y) unobserved(c r)
Makroökonomen erkennen diese Beziehungen als Konsum-Euler-Gleichung, als Kapitalnachfragegleichung, als Produktionsfunktion, als Kapitalakkumulationsgleichung bzw. als Bewegungsgesetz für die Produktivität.
Die Parameter haben Interpretation: {beta} ist der Diskontsatz, der üblicherweise bei etwa 0,95 liegt; {alpha} ist der Anteil des Kapitals am Einkommen, der üblicherweise bei etwa einem Drittel liegt; {delta} ist die Abschreibungsrate, üblicherweise 2,5 % pro Quartal; und {rho} ist die Persistenz des Technologieschocks. Priors werden verwendet, um diese Informationen in die Schätzung einfließen zu lassen.
Wir schätzen die Parameter dieses Modells anhand der detrendierten Ausgabe. Der Datensatz m1gdp.dta liefert den Logarithmus der Ausgabe.
. webuse m1gdp, clear
. describe
Contains data from https://www.stata-press.com/data/r17/m1gdp.dta
Observations: 223
Variables: 3 26 Mar 2020 02:49
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| t int %tq Quarterly time variable | ||
| ln_m1 float %9.0g ln(M1) monthly to quarterly by | ||
| averaging: M1 is Fred M1SL, Bil | ||
| of $ seas adj | ||
| ln_gdp float %9.0g ln(gdpc1) FRED GDP in Bil of 1996 | ||
| chained $ seas adj | ||
Der Befehl tsfilter extrahiert die Trendkomponente der Ausgabe. Wir verwenden einen Hodrick-Prescott-Filter und skalieren dann das Ergebnis um den Faktor 100 hoch. Die resultierende Skala ist so, dass ein Wert von 1 anzeigt, dass das BIP 1 % über seinem Trendwert liegt.
. tsfilter hp y = ln_gdp
. replace y = 100*y
(222 real changes made)
. tsline y, title("HP-detrended output")

Rezessionen sind mit einem Rückgang der Produktion unter den Trend verbunden, während Booms mit einem Anstieg der Produktion über den Trend verbunden sind.
Wir fahren mit der Parameterschätzung fort.
. bayes, prior({alpha}, beta(30,70)) ///
prior({beta}, beta(95,5)) ///
prior({delta}, beta(25,900)) ///
prior({rho}, beta(10, 10)) ///
rseed(20) dots saving(rbc_mcmc, replace): ///
dsgenl (1/c = {beta}*(1/F.c)*(1+f.r-{delta}) ) ///
(r = {alpha}*y/k ) ///
(y = z*k^({alpha}) ) ///
(f.k = y - c + (1-{delta})*k ) ///
(ln(f.z) = {rho}*ln(z) ) , ///
exostate(z) endostate(k) observed(y) unobserved(c r)
note: initial parameter vector set to means of priors.
Burn-in 2500 aaaaaaaaa1000aaaaaa...2000..... done
Simulation 10000 .........1000.........2000.........3000.........4000.........
5000.........6000.........7000.........8000.........9000.........10000 done
Model summary
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| beta | .9095501 .0392698 .001886 .9133171 .8231531 .9726171 | |
| delta | .0286052 .0054865 .000345 .0284 .0192159 .0404854 | |
| alpha | .2768864 .0451422 .002097 .2738962 .1964999 .3772306 | |
| rho | .7680742 .036755 .001813 .7680699 .6950177 .8412948 | |
| sd(e.z) | .9340691 .0458306 .001943 .9328126 .8502487 1.032548 | |
Der vorherige Mittelwert des Abzinsungssatzes {beta} ist 0,95; sein nachträglicher Mittelwert ist wenig verändert bei 0,91. Der priorisierte Mittelwert des Abschreibungssatzes {delta} ist 0,025; sein posteriorer Mittelwert ist mit 0,0286 wenig verändert. Der priorisierte Mittelwert von {alpha} ist 0,3; sein posteriorer Mittelwert ist mit 0,28 etwas niedriger. In der Zwischenzeit ist der posteriore Mittelwert von {rho} 0,77, viel größer als sein vorheriger Mittelwert von 0,5. Die Standardabweichung des Technologieschocks beträgt etwa 1.
Als nächstes berechnen wir Impuls-Antwort-Funktionen auf einen Technologieschock.
. bayesirf set bayes_irf2.irf, replace (file bayes_irf2.irf created) (file bayes_irf2.irf now active) . bayesirf create rbc_model, step(16) (file bayes_irf2.irf updated) . bayesirf graph irf, impulse(z) byopts(yrescale)
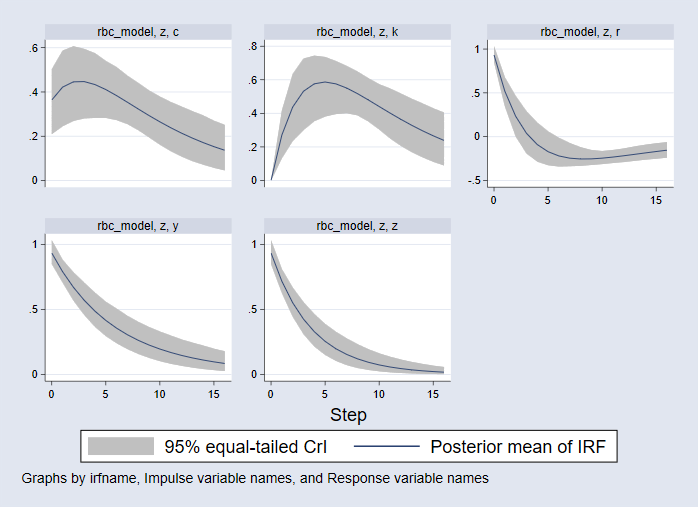
Die Einheiten der vertikalen Achse sind in prozentualen Abweichungen vom stationären Zustand. Die Einheiten der horizontalen Achse sind in der gleichen Zeitdauer wie die Daten, d. h. in Quartalen. Es werden 16 Stufen (4 Jahre) von Antworten dargestell
- Die Reaktion des Verbrauchs ist im linken oberen Feld aufgetragen. Der Verbrauch steigt beim Aufprall an und steigt dann in einem buckelförmigen Muster weiter an, bevor er wieder auf seinen Steady-State zurückfällt.
- Die Reaktion des Kapitalstocks ist oben in der Mitte dargestellt. Der Kapitalstock bewegt sich beim Aufprall nicht, steigt dann aber auf einen Spitzenwert von 0,6 % über dem Steady-State, bevor er wieder sinkt.
- Im rechten oberen Feld steigt der Zinssatz beim Aufprall und fällt dann; nach vier Quartalen sinkt er unter 0 und kehrt dann von unten zu seinem Steady-State zurück.
- Das linke untere Feld zeigt die Reaktion der Produktion; sie steigt beim Aufprall an und fällt dann monoton zurück auf ihren Steady-State.
- Das mittlere Feld unten zeigt die Reaktion der Technologie selbst. Auch sie steigt beim Aufprall an und fällt dann monoton auf ihren Steady-State zurück.
Genaue posteriore Mittelwerte und glaubwürdige Intervalle können mit der Bayesirf-Tabelle angezeigt werden. Im Folgenden wird die Reaktion des Konsums auf einen Technologieschock tabellarisch dargestellt.
. bayesirf table irf, impulse(z) response(c) Results from rbc_model
| (1) (2) (3) | ||
| step | irf Lower Upper | |
| 0 | .363699 .209593 .502829 | |
| 1 | .421867 .245335 .587063 | |
| 2 | .445802 .269215 .606835 | |
| 3 | .446962 .280481 .595064 | |
| 4 | .433453 .282893 .575041 | |
| 5 | .410962 .282863 .540024 | |
| 6 | .383436 .272859 .511974 | |
| 7 | .353574 .254899 .473345 | |
| 8 | .323189 .227486 .440766 | |
| 9 | .293459 .195011 .40683 | |
| 10 | .265119 .162333 .379442 | |
| 11 | .238595 .133143 .354938 | |
| 12 | .214099 .108564 .334151 | |
| 13 | .1917 .087822 .313609 | |
| 14 | .171372 .071785 .294301 | |
| 15 | .153031 .057275 .270277 | |
| 16 | .136556 .045631 .251522 | |
Nach einem Technologieschock mit einer Standardabweichung steigt der Konsum an und erreicht in der dritten Periode nach dem Schock einen Spitzenwert von 0,447 % über dem Steady-State-Wert.
