Nouveau dans 
Modèles DSGE linéaires et non linéaires bayésiens
Le préfixe bayes supporte désormais les commandes dsge et dsgenl pour ajuster les modèles bayésiens linéaires et non linéaires d’équilibre général stochastique dynamique (DSGE).
Les modèles DSGE sont populaires en macroéconomie et en finance pour modéliser de multiples séries temporelles. Ces modèles contiennent des systèmes d’équations linéaires ou non linéaires qui décrivent divers processus économiques. Les paramètres des modèles DSGE ont généralement une interprétation directe dans le contexte de la théorie économique et ont souvent des plages établies de valeurs plausibles. Ces plages (ou contraintes) doivent être intégrées dans l’estimation pour obtenir des résultats stables.
L’estimation bayésienne fournit un moyen naturel d’incorporer de telles contraintes en spécifiant diverses distributions antérieures pour les paramètres du modèle qui satisfont les contraintes.
Voyons comment cela fonctionne
Modèle DSGE linéaire
Un modèle DSGE consiste en un système d’équations qui relient les variables économiques, telles que l’inflation, le taux d’intérêt et l’écart de production, entre elles et aux variables d’état exogènes qui pilotent le système.
Points forts
- Modèles bayésiens d’équilibre général stochastique et dynamique
- Modèles linéaires et non linéaires
- Priors par défaut et personnalisés
- Contrôle flexible de l’échantillonnage MCMC
- Statistiques bayésiennes sommaires
- Diagnostics MCMC
- Chaînes multiples
- Fonctions de réponse aux impulsions
- Graphiques et tableaux des IRF
- Sauvegarde et comparaison des modèles
- Support complet des fonctions de posttimation bayésienne
Les équations peuvent être dynamiques dans deux sens : les décalages capturent le comportement rétrospectif, tandis que les valeurs futures attendues capturent le comportement prospectif. Les modèles DSGE peuvent être utilisés pour analyser les politiques, comme l’effet des chocs monétaires, des chocs fiscaux, etc.
L’estimation bayésienne comprend deux étapes : la spécification du modèle DSGE et la spécification des prieurs pour les paramètres du modèle DSGE.
Un petit modèle néo-keynésien comporte une équation d’investissement-économie (IS) qui lie l’écart de production au taux d’intérêt, une courbe de Phillips qui lie l’inflation à l’écart de production et une règle de Taylor qui lie le taux d’intérêt à l’inflation. En syntaxe Stata, le modèle ressemble à ceci :
( x = F.x - (r - F.p - z) , unobserved ) ///
( p = {beta}*F.p + {kappa}*x ) ///
( r = 1/{delta}*p + m ) ///
( F.z = {rhoz}*z, state ) ///
( F.m = {rhom}*m, state )
La première équation est une courbe IS, la deuxième est une courbe de Phillips et la troisième est une règle de Taylor. La quatrième équation est un choc IS, et la cinquième équation est un choc monétaire de règle de Taylor.
L’option non observée dans la courbe IS indique que nous traitons l’écart de production comme non observable. Nous ajustons le modèle aux données sur l’inflation et le taux d’intérêt.
Nous ajoutons une spécification préalable pour chaque paramètre. De nombreux paramètres DSGE ont des interprétations qui restreignent naturellement la gamme des valeurs admissibles. Le paramètre {beta} de la courbe de Phillips est un taux d’actualisation et doit être compris entre 0 et 1. Le paramètre {kappa} est un paramètre d’ajustement des prix, souvent considéré comme petit mais positif. Le paramètre {delta} est l’inverse du coefficient d’ajustement de l’inflation de la règle de Taylor, il doit donc être compris entre 0 et 1. En plus de ces restrictions, on peut avoir des priorités sur l’emplacement probable de la valeur du paramètre. Le taux d’actualisation se situe probablement autour de 0,95, le paramètre d’ajustement de l’inflation autour de 0,2, et le coefficient inverse d’ajustement de l’inflation autour de 0,66 (pour un coefficient de la règle de Taylor de 1,5). Les prieurs vous permettent d’incorporer cette information de manière explicite dans l’estimation.
Considérons les données sur le taux d’inflation et le taux des fonds fédéraux depuis 1955.
. webuse usmacro2 (Federal Reserve Economic Data - St. Louis Fed, 2017-01-15) . describe p r
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| p double %10.0g Growth rate of prices (GDPDEF) | ||
| r double %10.0g Federal funds rate (FEDFUNDS) | ||
| Variable | Obs Mean Std. dev. Min Max | |
| p | 2.44 3.236709 2.281433 -.6681431 11.60957 | |
| r | 2.44 5.035328 3.59569 .07 19.1 |
En rassemblant à la fois la spécification préalable et la spécification du modèle, notre commande d’estimation est la suivante
. bayes, prior({beta}, beta(95,5)) ///
prior({kappa}, beta(30,70)) ///
prior({delta}, beta(60,30)) ///
prior({rhoz}, beta(10,10)) ///
prior({rhom}, beta(10,10)) ///
rseed(17) : ///
dsge ( x = F.x - (r - F.p - z), unobserved) ///
( p = {beta}*F.p + {kappa}*x ) ///
( r = 1/{delta}*p + m ) ///
(F.z = {rhoz}*z, state ) ///
(F.m = {rhom}*m, state )
note: initial parameter vector set to means of priors.
Burn-in ...
Simulation ...
Model summary
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| beta | .9406005 .0243801 .001984 .9428465 .8869374 .9812481 | |
| kappa | .206337 .0327608 .001679 .2046031 .1470858 .273637 | |
| delta | .5832685 .0404188 .004897 .5835278 .497712 .6607058 | |
| rhoz | .9171911 .015764 .000978 .9170596 .8846393 .9467265 | |
| rhom | .561412 .0296339 .001667 .5621747 .5036024 .6184265 | |
| sd(e.z) | .5280986 .057275 .003639 .5255331 .4217194 .6467684 | |
| sd(e.m) | 2.161816 .1585077 .020872 2.141682 1.902066 2.533669 | |
Le résumé du modèle montre le modèle de vraisemblance et les spécifications des antériorités. Les prieurs pour tous les paramètres, sauf les écarts types, sont obligatoires. Dans le cas des modèles DSGE, cela est logique car les paramètres sont liés à la théorie économique. Par exemple, la priorité pour le facteur d’actualisation {beta} est beta avec des paramètres de forme 95 et 5. Les écarts types des chocs sur les variables d’état z et m se sont vus attribuer des prieurs gamma inverses par défaut.
Les résultats de l’estimation indiquent le nombre de périodes de rodage (2 500), la taille de l’échantillon MCMC (10 000), la taille de l’échantillon de données (244 périodes), la période d’échantillonnage (1955q1 à 2015q4), ainsi que le taux d’acceptation et l’efficacité du processus d’estimation. Le taux d’acceptation fait référence à la fraction des tirages MCMC qui a été acceptée. Les valeurs typiques pour l’échantillonneur Metropolis-Hastings utilisé sont de 20% à 30% ; notre taux d’acceptation est de 24%. L’efficacité est liée à l’autocorrélation des tirages MCMC et indique la vitesse à laquelle l’échantillonneur parcourt l’espace des paramètres. Notre efficacité moyenne est de 2,1 %.
La sortie de l’estimation affiche les moyennes des paramètres postérieurs, les écarts types, les médianes et les intervalles crédibles à queue égale. La moyenne postérieure de {beta} est de 0,94, très proche de sa moyenne antérieure de 0,95. La moyenne postérieure de {kappa} est d’environ 0,21, inférieure à la moyenne antérieure de 0,30. La moyenne postérieure de {delta} est de 0,58, inférieure à la moyenne antérieure de 0,66. Les deux chocs sont très persistants, avec des coefficients d’autocorrélation moyens a posteriori sur z et m de 0,92 et 0,56, respectivement. Les moyennes a posteriori des écarts types des chocs sont de 0,53 pour le choc IS z et de 2,16 pour le choc monétaire m de la règle de Taylor.
Toutes les fonctions de post-estimation bayésienne de Stata fonctionnent après bayes : dsge.
Nous pouvons tracer la densité postérieure du paramètre d’ajustement préalable {kappa}.
. bayesgraph kdensity {kappa}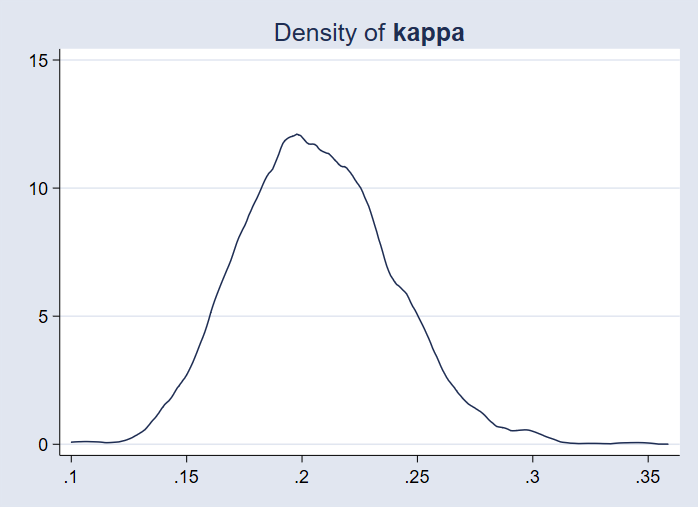
Nous pouvons tracer un ensemble complet de diagnostics pour{kappa}.
. bayesgraph diagnostics {kappa}
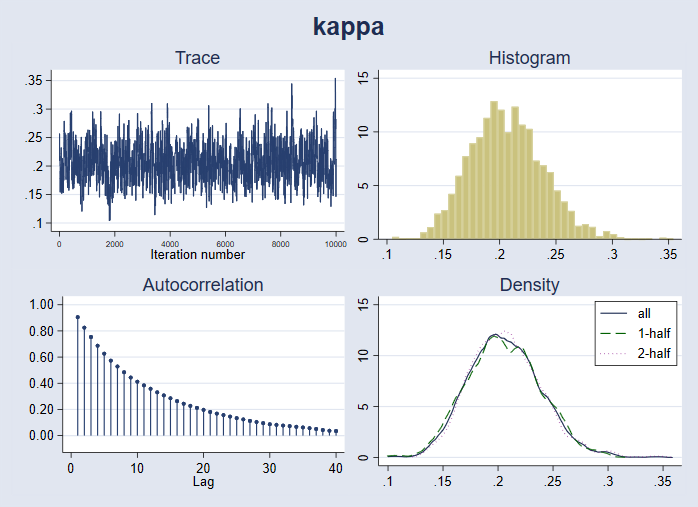
Nous pouvons ajouter la densité antérieure au tracé de la densité postérieure pour comparer visuellement l’antérieure et la postérieure.
. bayesgraph kdensity kappa, addplot(function Prior = betaden(30,70,x), ///
legend(on label(1 "Posterior")) lcolor(blue))

We can examine posterior densities of functions of model parameters, such as the Taylor rule coefficient 1/{delta}.
. bayesstats summary (1/{delta})
Posterior summary statistics MCMC sample size = 10,000
expr1 : 1/delta
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| expr1 | 1.722922 .1225577 .015302 1.713714 1.513533 2.009195 | |
La moyenne postérieure de 1/{delta} est de 1,7, supérieure à la moyenne antérieure de 1,5 et indiquant une forte réaction des taux d’intérêt aux variations de l’inflation.
Nous pouvons calculer les fonctions de réponse impulsionnelle bayésiennes. Tout d’abord, nous enregistrons les résultats MCMC dans un ensemble de données, nk_mcmc.dta. Nous pouvons le faire pendant l’estimation avec l’option saving() ou même après l’estimation en rejouant la commande bayes avec l’option saving().
. bayes, saving(nk_mcmc.dta, replace) note: file nk_mcmc.dta not found; file saved.
Une fois l’échantillon MCMC sauvegardé, nous pouvons construire des fonctions de réponse impulsionnelle avec la suite bayesirf. Cette suite de commandes étend irf pour permettre l’estimation bayésienne et est disponible après bayes : dsge, bayes : dsgenl, et bayes : var.
. bayesirf set bayes_irfs.irf, replace (file bayes_irfs.irf created) (file bayes_irfs.irf now active) . bayesirf create nk_model (file bayes_irfs.irf updated) . bayesirf graph irf, impulse(m) response(x p r m)

Le panneau supérieur gauche montre la réponse de la variable d’état monétaire m à un choc sur elle-même. Le panneau supérieur droit montre la réponse de l’inflation au choc : elle diminue puis revient de façon monotone à l’état d’équilibre. Le panneau inférieur gauche montre la réponse du taux d’intérêt : il augmente. Enfin, le panneau en bas à droite montre la réponse de l’écart de production : il passe en dessous de 0, indiquant une récession. Le choc monétaire contractionniste augmente donc le taux d’intérêt, réduit l’inflation et fait baisser la production.
Tout ceci et bien plus encore peut être réalisé avec la commande bayes : dsge.
Modèle DSGE non linéaire
Le préfixe bayes fonctionne également avec la commande dsgenl, qui estime les paramètres des modèles DSGE non linéaires par perturbation du premier ordre.
Ensuite, nous estimons les paramètres d’un modèle de croissance stochastique. Ce modèle comporte des équations pour la consommation, le taux d’intérêt réel, le PIB, le stock de capital et la productivité.
(1/c = {beta}*(1/F.c)*(1+F.r-{delta}) ) ///
(r = {alpha}*y/k ) ///
(y = z*k^({alpha}) ) ///
(f.k = y - c + (1-{delta})*k ) ///
(ln(f.z) = {rho}*ln(z) ) , ///
exostate(z) endostate(k) observed(y) unobserved(c r)
Les macroéconomistes reconnaîtront ces relations comme une équation d’Euler de la consommation, une équation de demande de capital, une fonction de production, une équation d’accumulation du capital et une loi de mouvement de la productivité, respectivement.
Les paramètres ont une interprétation : {beta} est le taux d’actualisation, généralement considéré comme étant d’environ 0,95 ; {alpha} est la part du capital dans le revenu, généralement considérée comme étant d’environ un tiers ; {delta} est le taux de dépréciation, généralement de 2,5% par trimestre ; et {rho} est la persistance du choc technologique. Les prieurs sont utilisés pour faire intervenir ces informations dans l’estimation.
Nous estimons les paramètres de ce modèle à l’aide de la production détendue. L’ensemble de données m1gdp.dta fournit le logarithme de la production.
. webuse m1gdp, clear
. describe
Contains data from https://www.stata-press.com/data/r17/m1gdp.dta
Observations: 223
Variables: 3 26 Mar 2020 02:49
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| t int %tq Quarterly time variable | ||
| ln_m1 float %9.0g ln(M1) monthly to quarterly by | ||
| averaging: M1 is Fred M1SL, Bil | ||
| of $ seas adj | ||
| ln_gdp float %9.0g ln(gdpc1) FRED GDP in Bil of 1996 | ||
| chained $ seas adj | ||
La commande tsfilter permet d’extraire la composante tendancielle de la production. Nous utilisons un filtre Hodrick-Prescott, puis nous augmentons le résultat d’un facteur 100. L’échelle résultante est telle qu’une valeur de 1 indique que le PIB est supérieur de 1% à sa valeur tendancielle.
. tsfilter hp y = ln_gdp
. replace y = 100*y
(222 real changes made)
. tsline y, title("HP-detrended output")

Les récessions sont associées à une baisse de la production en dessous de la tendance, tandis que les booms sont associés à une hausse de la production au-dessus de la tendance.
Nous procédons à l’estimation des paramètres.
. bayes, prior({alpha}, beta(30,70)) ///
prior({beta}, beta(95,5)) ///
prior({delta}, beta(25,900)) ///
prior({rho}, beta(10, 10)) ///
rseed(20) dots saving(rbc_mcmc, replace): ///
dsgenl (1/c = {beta}*(1/F.c)*(1+f.r-{delta}) ) ///
(r = {alpha}*y/k ) ///
(y = z*k^({alpha}) ) ///
(f.k = y - c + (1-{delta})*k ) ///
(ln(f.z) = {rho}*ln(z) ) , ///
exostate(z) endostate(k) observed(y) unobserved(c r)
note: initial parameter vector set to means of priors.
Burn-in 2500 aaaaaaaaa1000aaaaaa...2000..... done
Simulation 10000 .........1000.........2000.........3000.........4000.........
5000.........6000.........7000.........8000.........9000.........10000 done
Model summary
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| beta | .9095501 .0392698 .001886 .9133171 .8231531 .9726171 | |
| delta | .0286052 .0054865 .000345 .0284 .0192159 .0404854 | |
| alpha | .2768864 .0451422 .002097 .2738962 .1964999 .3772306 | |
| rho | .7680742 .036755 .001813 .7680699 .6950177 .8412948 | |
| sd(e.z) | .9340691 .0458306 .001943 .9328126 .8502487 1.032548 | |
La moyenne antérieure du taux d’actualisation {beta} est de 0,95 ; sa moyenne postérieure est peu modifiée à 0,91. La moyenne antérieure du taux de dépréciation {delta} est de 0,025 ; sa moyenne postérieure est peu modifiée à 0,0286. La moyenne antérieure de {alpha} est de 0,3 ; sa moyenne postérieure est légèrement inférieure à 0,28. Par ailleurs, la moyenne postérieure de {rho} est de 0,77, soit beaucoup plus que sa moyenne antérieure de 0,5. L’écart type du choc technologique est d’environ 1.
Nous calculons ensuite les fonctions de réponse impulsionnelle à un choc technologique.
. bayesirf set bayes_irf2.irf, replace (file bayes_irf2.irf created) (file bayes_irf2.irf now active) . bayesirf create rbc_model, step(16) (file bayes_irf2.irf updated) . bayesirf graph irf, impulse(z) byopts(yrescale)
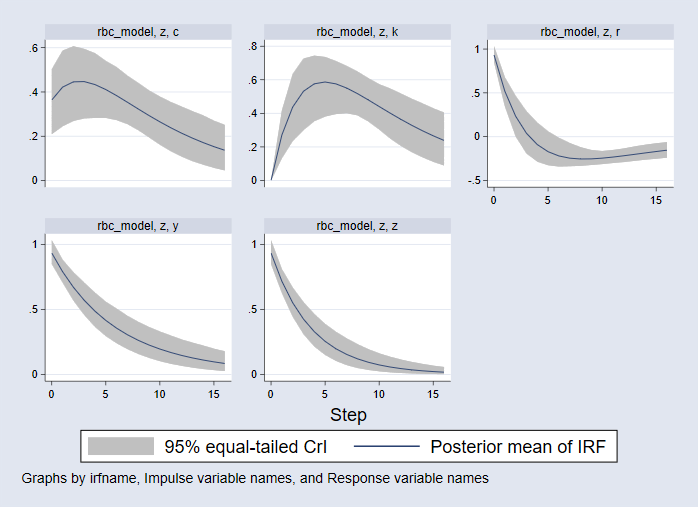
Les unités de l’axe vertical sont des écarts en pourcentage par rapport à l’état d’équilibre. Les unités de l’axe horizontal sont dans la même durée que les données, c’est-à-dire les trimestres. Nous traçons 16 étapes (4 ans) de réponses.
- La réponse de la consommation est représentée dans le panneau supérieur gauche. La consommation augmente au moment de l’impact, puis continue d’augmenter en forme de bosse avant de retomber à son état d’équilibre.
- La réponse du stock de capital est représentée dans le panneau supérieur médian. Le stock de capital ne bouge pas au moment de l’impact mais augmente ensuite jusqu’à un pic de 0,6 % au-dessus de son état d’équilibre avant de diminuer.
- Dans le panneau supérieur droit, le taux d’intérêt augmente au moment de l’impact, puis diminue ; il tombe en dessous de 0 après quatre trimestres, puis revient à son état d’équilibre par le bas.
- Le panneau inférieur gauche montre la réponse de la production ; elle augmente à l’impact et retombe ensuite de façon monotone vers son état d’équilibre.
- Le panneau inférieur médian représente la réponse de la technologie elle-même. Elle augmente également en fonction de l’impact, puis retombe de façon monotone vers son état stable.
Les moyennes postérieures exactes et les intervalles crédibles peuvent être visualisés avec le tableau bayesirf. Ci-dessous, nous présentons la réponse de la consommation à un choc technologique.
. bayesirf table irf, impulse(z) response(c) Results from rbc_model
| (1) (2) (3) | ||
| step | irf Lower Upper | |
| 0 | .363699 .209593 .502829 | |
| 1 | .421867 .245335 .587063 | |
| 2 | .445802 .269215 .606835 | |
| 3 | .446962 .280481 .595064 | |
| 4 | .433453 .282893 .575041 | |
| 5 | .410962 .282863 .540024 | |
| 6 | .383436 .272859 .511974 | |
| 7 | .353574 .254899 .473345 | |
| 8 | .323189 .227486 .440766 | |
| 9 | .293459 .195011 .40683 | |
| 10 | .265119 .162333 .379442 | |
| 11 | .238595 .133143 .354938 | |
| 12 | .214099 .108564 .334151 | |
| 13 | .1917 .087822 .313609 | |
| 14 | .171372 .071785 .294301 | |
| 15 | .153031 .057275 .270277 | |
| 16 | .136556 .045631 .251522 | |
Après un choc technologique d’un écart-type, la consommation augmente et culmine à 0,447 % au-dessus de sa valeur d’équilibre dans la troisième période après le choc.
