Novinky ve 
Bayesovská dynamická předpověď
Dynamické předpovídání je běžným nástrojem předpovídání po přizpůsobení vícerozměrných modelů časových řad, jako jsou vektorové autoregresní modely (VAR). Předpovídá výsledné hodnoty v aktuálním čase pomocí aktualizovaných (předpovězených) výsledných hodnot v předchozích časech. Nový příkaz bayesfcast počítá bayesovské dynamické předpovědi po fitování bayesovského modelu VAR pomocí příkazu bayes: var.
Bayesovské dynamické předpovědi vytvářejí celý vzorek předpovídaných hodnot výsledků v každém časovém okamžiku namísto jedné předpovědi jako v klasické analýze. Tento vzorek lze použít k zodpovězení různých modelovacích otázek, například jak dobře model předpovídá budoucí pozorování, aniž by se při odhadu nejistoty předpovědi uplatňoval předpoklad asymptotické normality. To je zvláště atraktivní pro malé soubory dat, u nichž může být předpoklad asymptotické normality podezřelý.
K výpočtu dynamických předpovědí a jejich uložení do aktuální datové sady můžete použít bayesfcast compute a pomocí bayesfcast graph je můžete zobrazit do grafu.
Podívejme se, jak to funguje
Pokračujeme makrodaty za USA z bayesovských VAR modelů, což jsou čtvrtletní data od prvního čtvrtletí roku 1954 do čtvrtého čtvrtletí roku 2010. Rádi bychom získali bayesovské dynamické prognózy inflace, mezery výstupu a sazby federálních fondů z bayesovského VAR modelu pro tyto proměnné.
Takto vypadají data.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

Výstup z příkazu bayes: var je dlouhý, proto jeho část níže vynecháme.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Podrobnosti o bayes: var a jeho výstupu naleznete v části Bayesovský model VAR.
K výpočtu bayesovských dynamických předpovědí používáme nový příkaz bayesfcast. Tento příkaz má dva dílčí příkazy. bayesfcast compute vypočítá prognózy a uloží je do aktuálního souboru dat jako nové proměnné. A příkaz bayesfcast graph vykreslí předpovědi.
Začněme nejjednodušší specifikací. Zadáme f_ jako předponu nových proměnných a semeno náhodného čísla pro reprodukovatelnost.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
bayesirf compute vytvoří nové proměnné obsahující různé souhrnné statistiky pro předpovědi. Na rozdíl od klasické analýzy neodpovídá bayesovská předpověď v určitém čase pouze jedné hodnotě, ale vzorku hodnot MCMC. Tyto hodnoty jsou pak shrnuty (jako průměry nebo mediány) a poskytují jedinou statistiku. Ve výchozím nastavení příkaz vypočítá pro každou výslednou proměnnou posteriorní průměry, posteriorní směrodatné odchylky a 95% rovnostranné intervaly spolehlivosti prognózy.
Vykresleme výchozí prognózy a jejich 95% rovnostranné intervaly spolehlivosti.
< br>
. bayesfcast graph f_inflation f_ogap f_fedfunds

Ve výchozím nastavení získáme jednookresní předpovědi. Později si ukážeme, jak vytvořit prognózy pro více období.
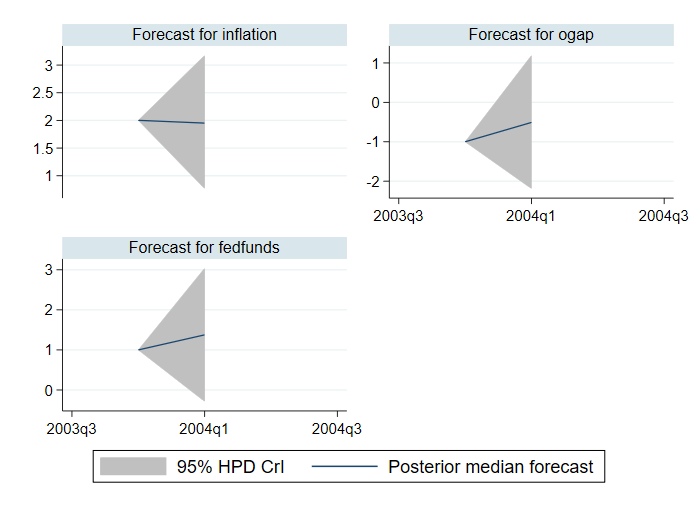
Namísto posteriorních středních prognóz a rovnoměrných intervalů spolehlivosti můžeme vypočítat posteriorní mediánové prognózy a intervaly spolehlivosti s nejvyšší posteriorní hustotou (HPD). Vypočítáme je a vykreslíme níže.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
Pokud chceme zkoumat trendy v předpovědích, potřebujeme více časových období. Níže například v možnosti step() příkazu bayesfcast compute zadáme 28 období.
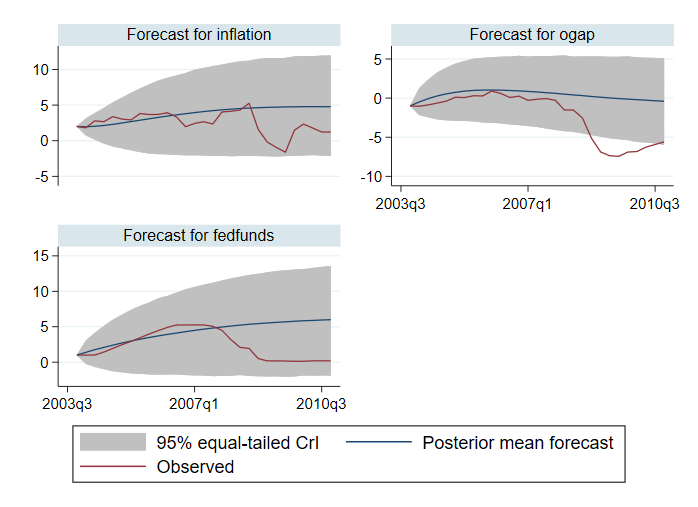
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Porovnáme naše předpovědi s pozorovanými hodnotami. Zdá se, že prognózy dobře předpovídají výsledky až do roku 2007. Poté se jejich výsledky zhoršují. Například 95% věrohodné intervaly pro mezeru výstupu neobsahují pozorované hodnoty po část časového horizontu.
Po analýze odstraníme soubor simulace MCMC uložený pomocí bayes: var.
. erase bvarsim.dta
