Újdonságok a  -ben
-ben
Bayesi dinamikus előrejelzés
A dinamikus előrejelzés gyakori előrejelzési eszköz a többváltozós idősoros modellek, például a vektor-autoregresszív (VAR) modellek illesztése után. Az előző idők frissített (előre jelzett) eredményértékeinek felhasználásával megjósolja a kimeneti értékeket egy adott időpontban. Az új bayesfcast parancs kiszámítja a bayesi dinamikus előrejelzéseket, miután egy bayesi VAR modellt illesztett a bayes: var paranccsal.
A Bayes-i dinamikus előrejelzések az előrejelzett eredményértékek teljes mintáját állítják elő minden egyes időpontban egyetlen előrejelzés helyett, mint a klasszikus elemzésben. Ez a minta felhasználható különböző modellezési kérdések megválaszolására, például arra, hogy a modell mennyire jósolja meg a jövőbeni megfigyeléseket anélkül, hogy az aszimptotikus normalitás feltételezését elvégezné az előrejelzési bizonytalanság becslésénél. Ez különösen vonzó a kis adatkészletek esetében, amelyek esetében az aszimptotikus normalitás feltételezése gyanús lehet.
A bayesfcast compute kiszámíthatja a dinamikus előrejelzéseket és elmentheti azokat az aktuális adatkészletbe, és a bayesfcast graph segítségével ábrázolhatja őket.
Lássuk hogyan működik
Folytatjuk a Bayes-i VAR modellek amerikai makrodatait, amelyek 1954 első negyedévétől 2010 negyedik negyedévéig tartó negyedéves adatok. Szeretnénk Bayes-féle dinamikus előrejelzéseket kapni az inflációról, a kibocsátási résről és a szövetségi alapok arányáról egy Bayes-i VAR-modell alapján ezekre a változókra.
Így néznek ki az adatok.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

A bayes: var parancs kimenete hosszú, ezért az alábbiakban néhányat kihagyunk.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Lásd a Bayesian VAR modellt a bayes: var és kimenetének részleteiről. Az új bayesfcast paranccsal kiszámoljuk a Bayesi dinamikus előrejelzéseket. Ennek a parancsnak két alparancsa van. A bayesfcast compute kiszámítja az előrejelzéseket, és új változóként menti őket az aktuális adatkészletbe. És a bayesfcast graph ábrázolja az előrejelzéseket.
Kezdjük a legegyszerűbb specifikációval. Megadjuk az f_ értéket az új változók előtagjaként, és a véletlenszámú magot a reprodukálhatóság érdekében.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
A bayesirf compute új változókat hoz létre, amelyek különböző összefoglaló statisztikákat tartalmaznak az előrejelzésekhez. A klasszikus elemzéssel ellentétben a Bayes-előrejelzés egy adott időpontban nemcsak egy értéknek felel meg, hanem az MCMC-értékek mintájának is. Ezeket az értékeket ezután (átlagként vagy mediánként) összefoglalva egyetlen statisztikát kapunk. Alapértelmezés szerint a parancs kiszámítja az egyes kimeneti változók előrejelzéséhez a hátsó átlagokat, a hátsó szórásokat és a 95% -os, azonos farokú hiteles intervallumokat.
Ábrázoljuk az alapértelmezett előrejelzéseket és azok 95% -os egyenrangú hiteles sávjait.
< br>
. bayesfcast graph f_inflation f_ogap f_fedfunds

Alapértelmezés szerint egyperiódusos előrejelzéseket kapunk. Később bemutatjuk, hogyan lehet több periódusos előrejelzéseket készíteni.
A hátsó átlag előrejelzések és az egyenlő farkú hiteles intervallumok helyett kiszámíthatjuk a hátsó medián előrejelzéseket és a legmagasabb posterior sűrűség (HPD) hiteles intervallumokat.
Az alábbiakban kiszámoljuk és ábrázoljuk őket.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
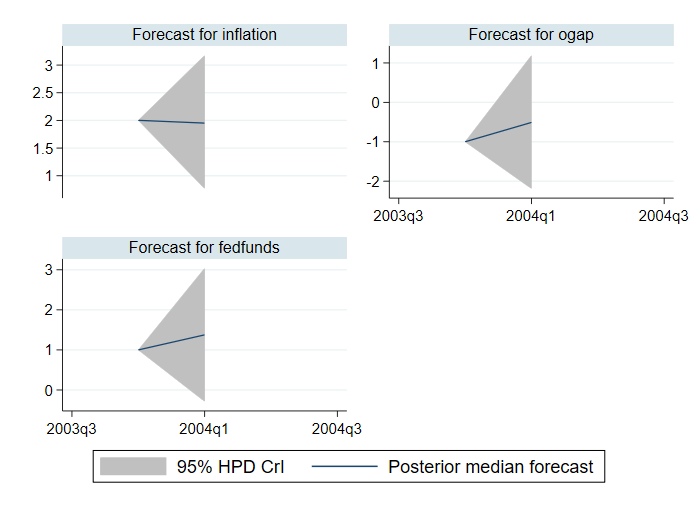
Ha meg akarjuk vizsgálni az előrejelzések trendjeit, több időtartamra van szükségünk. Például az alábbiakban 28 periódust adunk meg a bayesfcast compute step() opciójában.
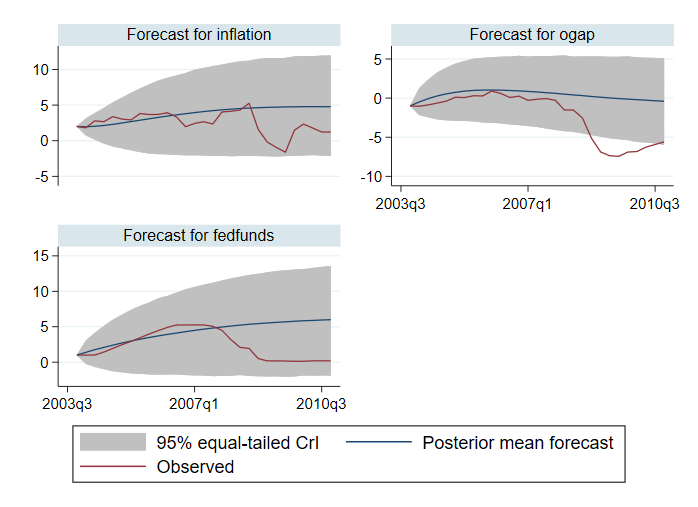
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Összehasonlítjuk előrejelzéseinket a megfigyelt értékekkel. Úgy tűnik, hogy az előrejelzések jól teljesítik az eredményeket 2007-ig. Ezt követően gyengén teljesítenek. Például a kimeneti rés 95% -os hiteles intervallumai nem tartalmazzák az időhorizont egy részében megfigyelt értékeket.
Az elemzés után eltávolítjuk a bayes: var. Által elmentett MCMC szimulációs fájlt.
. erase bvarsim.dta
