Nouveau dans 
Prévision dynamique bayésienne
La prévision dynamique est un outil de prédiction courant après l’ajustement de modèles de séries chronologiques multivariées, tels que les modèles vectoriels autorégressifs (VAR). Elle prédit les valeurs de résultats à un moment donné en utilisant les valeurs de résultats mises à jour (prédites) à des moments précédents. La nouvelle commande bayesfcast calcule des prévisions dynamiques bayésiennes après avoir ajusté un modèle VAR bayésien à l’aide de la commande bayes : var.
Les prévisions dynamiques bayésiennes produisent un échantillon complet de valeurs de résultats prédits à chaque point temporel au lieu d’une seule prédiction comme dans l’analyse classique. Cet échantillon peut être utilisé pour répondre à diverses questions de modélisation, telles que la façon dont le modèle prédit les observations futures sans faire l’hypothèse de normalité asymptotique lors de l’estimation de l’incertitude de la prévision. Ceci est particulièrement intéressant pour les petits ensembles de données pour lesquels l’hypothèse de normalité asymptotique peut être suspecte.
Vous pouvez utiliser bayesfcast compute pour calculer des prévisions dynamiques et les enregistrer dans l’ensemble de données actuel, et vous pouvez les représenter graphiquement en utilisant bayesfcast graph.
Points forts
- Graphique des prévisions dynamiques
- Sauvegarder les prévisions dynamiques dans l’ensemble de données actuel
- Spécifier l’horizon de prédiction
- Calculer les moyennes ou médianes postérieures des prévisions
- Calculer les écarts types postérieurs
- Calcul des intervalles crédibles a posteriori
Voyons comment cela fonctionne
Nous poursuivons avec les macrodonnées américaines issues de modèles VAR bayésiens, qui sont des données trimestrielles allant du premier trimestre de 1954 au quatrième trimestre de 2010. Nous souhaitons obtenir des prévisions dynamiques bayésiennes de l’inflation, de l’écart de production et du taux des fonds fédéraux à partir d’un modèle VAR bayésien pour ces variables.
Voici à quoi ressemblent les données.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

La sortie de la commande bayes : var est longue, nous en omettons donc une partie ci-dessous.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Voir Modèle VAR bayésien pour plus de détails sur bayes : var et ses résultats.
Nous utilisons la nouvelle commande bayesfcast pour calculer les prévisions dynamiques bayésiennes. Cette commande comporte deux sous-commandes. bayesfcast compute calcule les prévisions et les enregistre dans l’ensemble de données actuel en tant que nouvelles variables. Et bayesfcast graph trace les prévisions.
Commençons par la spécification la plus simple. Nous spécifions f_ comme préfixe pour les nouvelles variables et une graine de nombre aléatoire pour la reproductibilité.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
bayesirf compute crée de nouvelles variables contenant diverses statistiques sommaires pour les prévisions. Contrairement à l’analyse classique, une prévision bayésienne à un moment donné ne correspond pas à une seule valeur mais à un échantillon de valeurs MCMC. Ces valeurs sont ensuite résumées (en tant que moyennes ou médianes) pour fournir une statistique unique. Par défaut, la commande calcule les moyennes postérieures, les écarts types postérieurs et les intervalles crédibles à 95 % à queue égale pour la prévision de chaque variable de résultat.
Traçons les prévisions par défaut et leurs bandes crédibles à 95% à queue égale.
< br>
. bayesfcast graph f_inflation f_ogap f_fedfunds

Par défaut, nous obtenons des prévisions à une période. Nous montrerons plus tard comment créer des prévisions avec plus de périodes.
Au lieu des prévisions moyennes postérieures et des intervalles crédibles à queue égale, nous pouvons calculer les prévisions médianes postérieures et les intervalles crédibles de la densité postérieure la plus élevée (HPD). Nous les calculons et les représentons ci-dessous.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
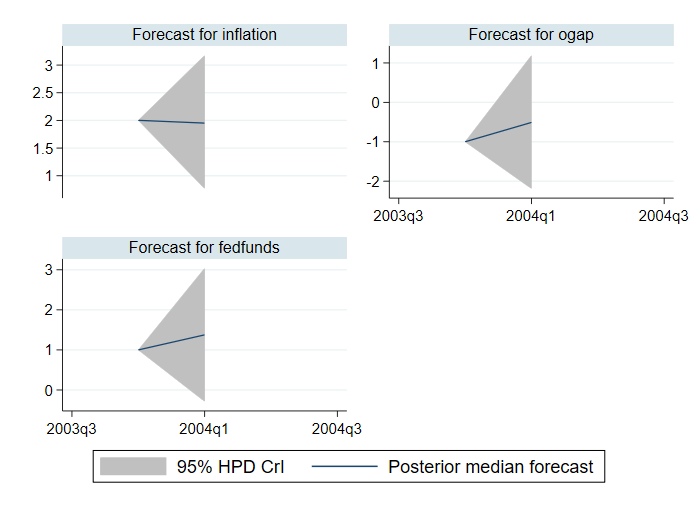
Si nous voulons explorer les tendances dans les prévisions, nous avons besoin de plus de périodes. Par exemple, ci-dessous, nous spécifions 28 périodes dans l’option step() de bayesfcast compute.
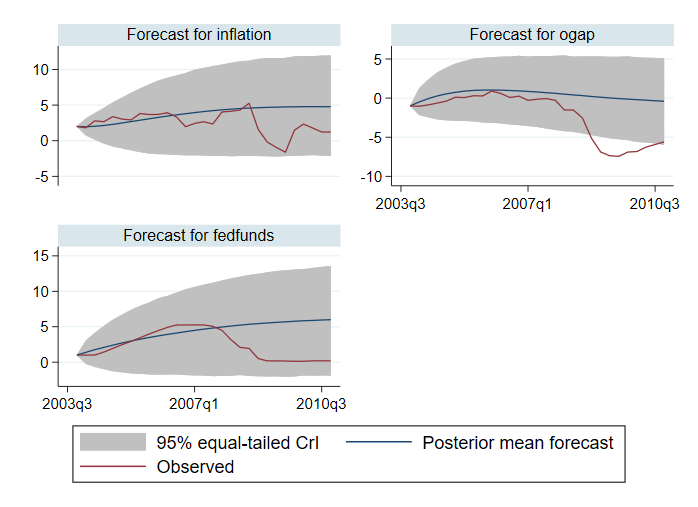
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Nous comparons nos prévisions avec les valeurs observées. Les prévisions semblent bien réussir à prédire les résultats jusqu’en 2007. Après cela, elles sont peu performantes. Par exemple, les intervalles crédibles à 95% pour l’écart de production ne contiennent pas les valeurs observées pour une partie de l’horizon temporel.
Après l’analyse, nous supprimons le fichier de simulation MCMC enregistré par bayes : var.
. erase bvarsim.dta
