Ново в 
Бейсовско динамично прогнозиране
Динамичното прогнозиране е често срещан инструмент за прогнозиране, след като се приложат многомерни модели на времеви редове, като например векторни авторегресионни модели (VAR). При него се прогнозират стойностите на резултатите в текущия момент, като се използват актуализирани (прогнозирани) стойности на резултатите в предишни моменти. Новата команда bayesfcast изчислява динамични прогнози по метода на Байес след монтиране на байесов VAR модел с помощта на командата bayes: var.
Байесовите динамични прогнози създават цяла извадка от прогнозирани стойности на резултатите във всеки момент, вместо една-единствена прогноза, както е при класическия анализ. Тази извадка може да се използва за отговор на различни въпроси, свързани с моделирането, като например колко добре моделът предсказва бъдещите наблюдения, без да се прави допускане за асимптотична нормалност при оценяване на прогнозната неопределеност. Това е особено привлекателно за малки набори от данни, за които допускането за асимптотична нормалност може да е подозрително.
Можете да използвате bayesfcast compute, за да изчислите динамични прогнози и да ги запазите в текущата съвкупност от данни, както и да ги изобразите на графики, като използвате bayesfcast graph.
Акценти
- Графични динамични прогнози
- Записване на динамични прогнози в текущия набор от данни
- Посочете хоризонта на прогнозиране
- Изчисляване на апостериорни средни стойности или медиани на прогнозите
- Изчисляване на апостериорните стандартни отклонения
- Изчисляване на апостериорни доверителни интервали
Нека видим как работи
Продължаваме с макроданните за САЩ от моделите на Бейс VAR, които са тримесечни данни от първото тримесечие на 1954 г. до четвъртото тримесечие на 2010 г. Бихме искали да получим бейсовски динамични прогнози за инфлацията, производствената разлика и лихвения процент по федералните фондове от бейсовски VAR модел за тези променливи.
Ето как изглеждат данните.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

Изходът от командата bayes: var е дълъг, затова по-долу ще пропуснем част от него.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Вижте Bayesian VAR model за подробности относно bayes: var и неговите резултати.
Използваме новата команда bayesfcast за изчисляване на динамични прогнози по метода на Бейс. Тази команда има две подкоманди. bayesfcast compute изчислява прогнозите и ги записва в текущия набор от данни като нови променливи. А bayesfcast graph изобразява прогнозите.
Нека да започнем с най-простата спецификация. Посочваме f_ като префикс за новите променливи и случайно число за възпроизводимост.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
bayesirf compute създава нови променливи, съдържащи различни обобщени статистики за прогнозите. За разлика от класическия анализ, прогнозата на Байес в определен момент съответства не само на една стойност, а на извадка от MCMC стойности. След това тези стойности се обобщават (като средни стойности или медиани), за да се получи една статистика. По подразбиране командата изчислява апостериорни средни стойности, апостериорни стандартни отклонения и 95% равни доверителни интервали за прогнозата за всяка резултативна променлива.
Нека изведем графиката на прогнозите по подразбиране и техните 95% равностойни доверителни интервали.
< br>
. bayesfcast graph f_inflation f_ogap f_fedfunds

По подразбиране получаваме прогнози за един период. По-късно ще покажем как да създадем прогнози за повече периоди.
Вместо апостериорни средни прогнози и равностойни доверителни интервали можем да изчислим апостериорни медианни прогнози и доверителни интервали с най-висока апостериорна плътност (HPD). Изчисляваме ги и ги изобразяваме по-долу.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
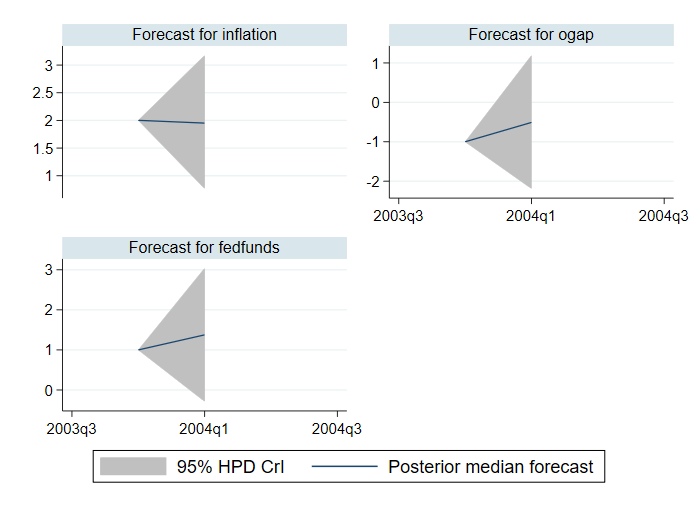
Ако искаме да проучим тенденциите в прогнозите, са ни необходими повече периоди от време. Например, по-долу сме посочили 28 периода в опцията step() на bayesfcast compute.
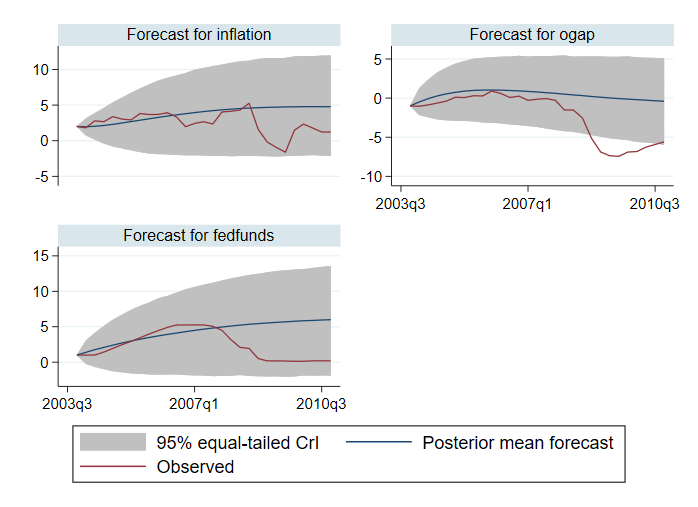
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Сравняваме нашите прогнози с наблюдаваните стойности. Изглежда, че прогнозите се справят добре с прогнозирането на резултатите до 2007 г. След това те се представят зле. Например 95%-ните доверителни интервали за производствената разлика не съдържат наблюдаваните стойности за част от времевия хоризонт.
След анализа премахваме файла за MCMC симулация, запазен от bayes: var.
. erase bvarsim.dta
