Neu in 
Bayessche dynamische Vorhersage
Die dynamische Vorhersage ist ein gängiges Vorhersagewerkzeug nach der Anpassung von multivariaten Zeitreihenmodellen, wie z. B. vektorautoregressiven (VAR) Modellen. Es sagt Ergebniswerte zu einem aktuellen Zeitpunkt voraus, indem es aktualisierte (vorhergesagte) Ergebniswerte zu früheren Zeitpunkten verwendet. Der neue Befehl bayesfcast berechnet dynamische Bayes’sche Prognosen nach der Anpassung eines Bayes’schen VAR-Modells mit dem Befehl bayes: var.
Dynamische Bayes’sche Vorhersagen erzeugen eine ganze Stichprobe von vorhergesagten Ergebniswerten zu jedem Zeitpunkt anstelle einer einzelnen Vorhersage wie bei der klassischen Analyse. Diese Stichprobe kann verwendet werden, um verschiedene Modellierungsfragen zu beantworten, z. B. wie gut das Modell zukünftige Beobachtungen vorhersagt, ohne die asymptotische Normalitätsannahme bei der Schätzung der Prognoseunsicherheit zu machen. Dies ist besonders attraktiv für kleine Datensätze, für die die asymptotische Normalitätsannahme verdächtig sein kann.
Sie können bayesfcast compute verwenden, um dynamische Vorhersagen zu berechnen und im aktuellen Datensatz zu speichern, und Sie können sie mit bayesfcast graph grafisch darstellen.
Zeigen Sie, wie es funktioniert
Wir fahren mit den US-Makrodaten aus Bayes’schen VAR-Modellen fort, die vierteljährliche Daten vom ersten Quartal 1954 bis zum vierten Quartal 2010 sind. Wir möchten Bayes’sche dynamische Prognosen der Inflation, der Produktionslücke und des Leitzinses aus einem Bayes’schen VAR-Modell für diese Variablen erhalten.
So sehen die Daten aus.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

Die Ausgabe des Befehls bayes: var ist lang, daher lassen wir im Folgenden einen Teil davon weg.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Siehe Bayes’sches VAR-Modell für Details über bayes: var und seine Ausgabe.
Wir verwenden den neuen Befehl bayesfcast, um dynamische Bayes’sche Prognosen zu berechnen. Dieser Befehl hat zwei Unterbefehle. bayesfcast compute berechnet die Prognosen und speichert sie im aktuellen Datensatz als neue Variablen. Und bayesfcast graph stellt die Prognosen dar.
Beginnen wir mit der einfachsten Spezifikation. Wir geben f_ als Präfix für die neuen Variablen und einen Zufallszahlen-Seed für die Reproduzierbarkeit an.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
bayesirf compute erstellt neue Variablen, die verschiedene zusammenfassende Statistiken für Prognosen enthalten. Anders als bei der klassischen Analyse entspricht eine Bayes’sche Prognose zu einem bestimmten Zeitpunkt nicht nur einem Wert, sondern einer Stichprobe von MCMC-Werten. Diese Werte werden dann zusammengefasst (als Mittelwerte oder Mediane), um eine einzelne Statistik zu erstellen. Standardmäßig berechnet der Befehl Posterior-Mittelwerte, Posterior-Standardabweichungen und 95 % gleichabschließende Glaubwürdigkeitsintervalle für die Prognose für jede Ergebnisvariable.
Lassen Sie uns die Standardprognosen und ihre 95%-ig gleichschwänzigen Glaubwürdigkeitsbänder einzeichnen.
< br>
. bayesfcast graph f_inflation f_ogap f_fedfunds

Standardmäßig erhalten wir Prognosen mit einer Periode. Wir zeigen später, wie Sie Prognosen mit mehr Perioden erstellen können.
Anstelle von Posterior-Mittelwertprognosen und gleichabschließenden Glaubwürdigkeitsintervallen können wir Posterior-Median-Prognosen und Glaubwürdigkeitsintervalle der höchsten Posterior-Dichte (HPD) berechnen. Wir berechnen sie unten und stellen sie dar.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
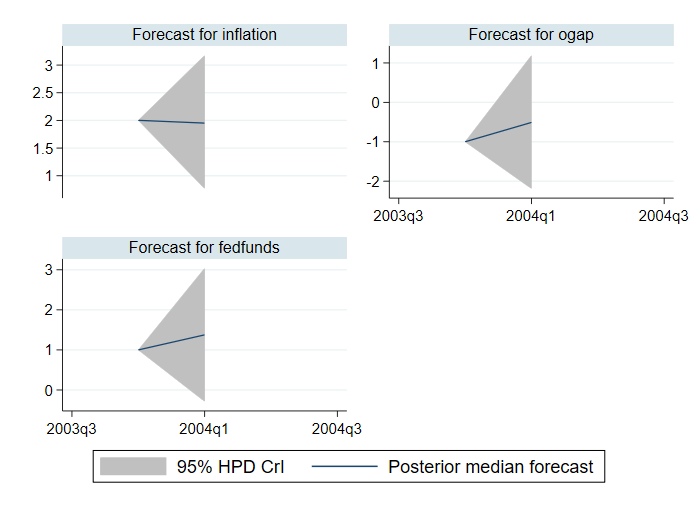
Wenn wir Trends in den Prognosen untersuchen wollen, benötigen wir mehr Zeiträume. Unten geben wir zum Beispiel 28 Perioden in der Option step() von bayesfcast compute an.
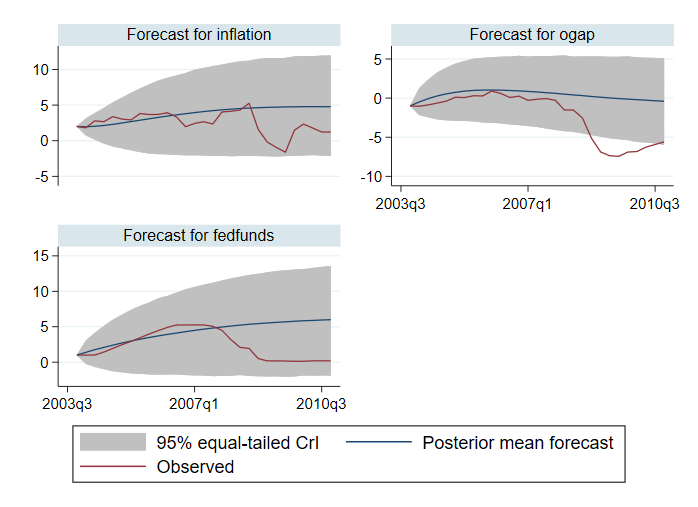
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Wir vergleichen unsere Prognosen mit den beobachteten Werten. Die Prognosen scheinen die Ergebnisse bis zum Jahr 2007 gut vorherzusagen. Danach schneiden sie schlecht ab. Beispielsweise enthalten die 95%-Glaubwürdigkeitsintervalle für die Produktionslücke für einen Teil des Zeithorizonts nicht die beobachteten Werte.
Nach der Analyse entfernen wir die von bayes gespeicherte MCMC-Simulationsdatei: var.
. erase bvarsim.dta
