Нове в 
Байєсівське динамічне прогнозування
Динамічне прогнозування є звичайним інструментом прогнозування після встановлення багатовимірних моделей часових рядів, таких як векторні моделі авторегресії (VAR). Він прогнозує значення результатів у поточний момент, використовуючи оновлені (передбачувані) значення результатів у попередній час. Нова команда bayesfcast обчислює байєсівські динамічні прогнози після встановлення байєсівської моделі VAR за допомогою команди bayes: var.
Байєсівські динамічні прогнози створюють цілу вибірку передбачуваних значень результатів у кожен момент часу замість одного передбачення, як у класичному аналізі. Цей зразок можна використовувати для відповіді на різні питання моделювання, наприклад, наскільки добре модель прогнозує майбутні спостереження, не роблячи припущення асимптотичної нормальності при оцінці невизначеності прогнозу. Це особливо привабливо для невеликих наборів даних, для яких можна підозрювати припущення асимптотичної нормальності.
Ви можете використовувати bayesfcast compute для обчислення динамічних прогнозів і збереження їх у поточному наборі даних, а також ви можете побудувати їх у графіку, використовуючи bayesfcast graph.
Давайте подивимося, як це працює
Ми продовжуємо використовувати макродані США з байєсівських моделей VAR, які є квартальними даними з першого кварталу 1954 року по четвертий квартал 2010 року. Ми хотіли б отримати байєсівські динамічні прогнози інфляції, розриву виробництва та ставки федерального фонду з байєсівського VAR модель для цих змінних.
Ось як виглядають дані.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

The output from the bayes: var command is long, so we omit some of it below.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Дивіться байєсівську модель VAR, щоб дізнатися більше про bayes: var та його вихід.
Ми використовуємо нову команду bayesfcast для обчислення байєсівських динамічних прогнозів. Ця команда має дві підкоманди. bayesfcast compute обчислює прогнози та зберігає їх у поточному наборі даних як нові змінні. А bayesfcast graph накреслює прогнози.
Почнемо з найпростішої специфікації. Ми вказуємо f_ як префікс для нових змінних і початкове число випадкових чисел для відтворюваності.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
bayesirf compute створює нові змінні, що містять різні підсумкові статистичні дані для прогнозів. На відміну від класичного аналізу, байєсівський прогноз на певний час відповідає не лише одному значенню, а вибірці значень MCMC. Ці значення потім підсумовуються (як середні чи медіани), щоб отримати єдину статистику. За замовчуванням команда обчислює апостеріорні середні значення, апостеріорні стандартні відхилення та 95% рівнохвостих вірогідних інтервалів для прогнозу для кожної змінної результату.
Давайте побудуємо прогнози за замовчуванням та їх 95% рівнохвостих достовірних діапазонів.
< br>
. bayesfcast graph f_inflation f_ogap f_fedfunds

За замовчуванням ми отримуємо прогнози на один період. Пізніше ми покажемо, як створювати прогнози з більшою кількістю періодів.
Замість апостеріорних середніх прогнозів і достовірних інтервалів із рівним хвостом ми можемо обчислити апостеріорні медіанні прогнози та достовірні інтервали найвищої апостеріорної щільності (HPD). Нижче ми їх обчислюємо та зображуємо.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
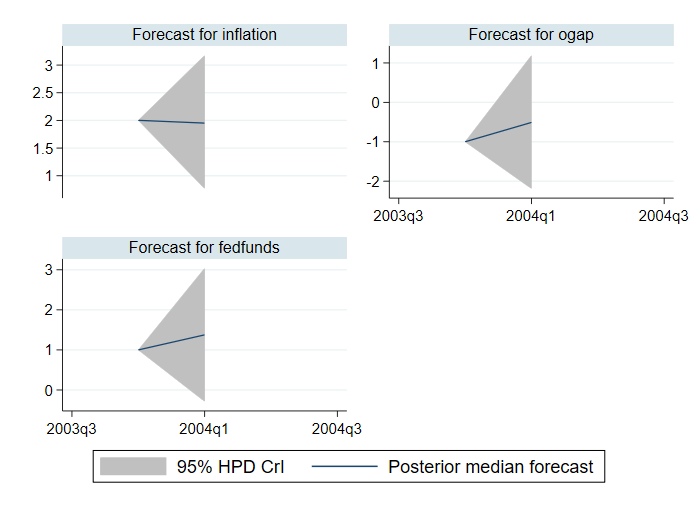
Якщо ми хочемо досліджувати тенденції в прогнозах, нам потрібно більше періодів часу. Наприклад, нижче ми вказуємо 28 точок у параметрі step() для bayesfcast compute.
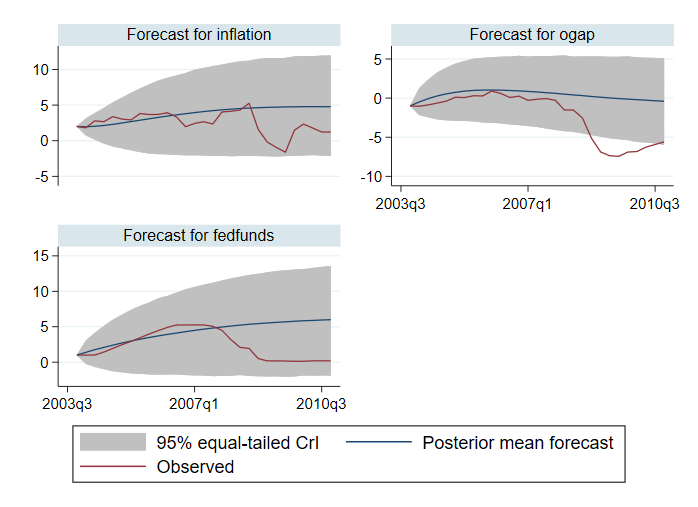
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Ми порівнюємо наші прогнози з спостережуваними значеннями. Здається, прогнози добре спрогнозують результати до 2007 року. Після цього вони працюють погано. Наприклад, 95% вірогідні інтервали для розриву виробництва не містять спостережуваних значень для частини часового горизонту.
Після аналізу ми видаляємо файл моделювання MCMC, збережений bayes: var.
. erase bvarsim.dta
