Nouveautés de la version 12.3

Lancement de la version 12.3 du langage Wolfram et de Mathematica

Regardez ce que nous avons fait en cinq mois !

Il est difficile de croire que nous faisons cela depuis 35 ans, construisant une tour de plus en plus haute d’idées et de technologies qui nous permettent d’aller toujours plus loin. Auparavant, nous ne publiions les résultats de nos efforts que tous les deux ans. Mais récemment, nous avons commencé à publier des versions incrémentielles (« .1″) qui présentent nos dernières réalisations en matière de R&D – à la fois sous leur forme complète et en partie sous forme d' »attractions à venir » – beaucoup plus fréquemment.

Nous avons publié la Version 12.2 on December 16, 2020. le 16 décembre 2020. Et aujourd’hui, à peine cinq mois plus tard, nous publions la version 12.3. La version 12.3 comporte quelques avancées et de nouvelles orientations majeures. Mais la majeure partie du contenu de la version 12.3 vise simplement à rendre Wolfram Language et Mathematica meilleurs, plus fluides et plus pratiques à utiliser. Les choses sont plus rapides. Davantage de cas « Mais qu’en est-il de ___ ? » sont traités. Les grands cadres sont plus complets. Et il y a beaucoup de nouvelles commodités.

On y trouve également les premiers éléments de ce qui deviendra à l’avenir des structures à grande échelle. Des fonctions précoces – déjà très utiles en soi – qui, dans les prochaines versions, deviendront des éléments de structures majeures à l’échelle du système.

Une façon d’évaluer une version est de parler du nombre de nouvelles fonctions qu’elle contient. Pour la version 12.3, ce nombre est de 111 (soit environ 5 nouvelles fonctions par semaine de développement). C’est un niveau de productivité de la R&D très impressionnant. Mais, en particulier pour la version 12.3, ce n’est qu’une partie de l’histoire ; il y a également 1190 corrections de bogues (environ un quart pour les bogues signalés en externe), et 105 fonctions substantiellement mises à jour et améliorées.

Incremental releases are part of our commitment to open development. Nous avons également partagé davantage de types de fonctionnalités sous forme de code source ouvert (notamment plus de 300 nouvelles fonctions dans le Wolfram Function Repository). Et nous avons continué à diffuser en direct nos processus de conception internes, ce qui est unique. Pour la version 12.3, il est à nouveau possible de voir où et comment les décisions de conception ont été prises, et le raisonnement qui les sous-tend. Notre communauté nous a également fait part de ses commentaires (souvent en temps réel pendant les livestreams), ce qui a permis d’améliorer considérablement la version 12.3 que nous livrons aujourd’hui.

À propos, lorsque nous parlons de la « version 12.3 » du Wolfram Language et de Mathematica, nous parlons de l’ordinateur de bureau, du cloud et du moteur: les trois versions sont publiées aujourd’hui.

Beaucoup de petites commodités nouvelles

Qu’est-ce qui devrait « fonctionner » ? Qu’est-ce qui devrait être plus facile ? Depuis la version 1.0, nous avons travaillé dur pour trouver les petites commodités que nous pouvons ajouter pour rendre le Wolfram Language toujours plus simple.

La version 12.3 contient notre dernier lot de commodités, réparties dans de nombreuses parties du langage. Une nouvelle dynamique est apparue dans cette version : les fonctions qui ont été essentiellement « prototypées » dans le Wolfram Function Repository, puis « mises à niveau » pour être intégrées au système.

Voici un premier exemple d’une nouvelle fonction pratique : SolveValues. La fonction Solve— initialement introduite dans la version 1.0 — a une façon très flexible de représenter ses résultats, qui permet différents nombres de variables, différents nombres de solutions, etc.

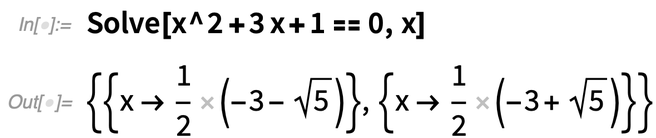
Mais souvent, vous êtes heureux d’assumer une structure fixe pour la solution, et vous voulez juste connaître les valeurs des variables. Et c’est ce que SolveValues donne :

Au fait, il existe aussi un NSolveValues qui donne des valeurs numériques approximatives :

Un autre exemple de nouvelle fonction pratique est NumberDigit. Disons que vous voulez le 10e chiffre de π, vous pouvez toujours utiliser RealDigits et ensuite choisir le chiffre que vous voulez :

Mais maintenant vous pouvez aussi utiliser simplement NumberDigit (où maintenant par « 10ème chiffre » nous supposons que vous voulez dire le coefficient de 10-10) :

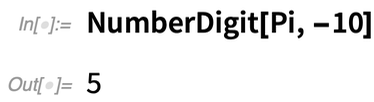Dans la version 1.0, nous n’avions que Sort. Dans la version 10.3 (2015), nous avons ajouté AlphabeticSort, puis dans la version 11.1 (2017), NumericalSort. Maintenant, dans la version 12.3, pour compléter cette famille de types de tri par défaut, nous ajoutons LexicographicSort. Le tri par défaut (tel que produit par Sort) est :

Mais voici le véritable ordre lexicographique, comme celui que l’on trouve dans un dictionnaire :

Une autre petite fonction nouvelle dans la version 12.3 est StringTakeDrop :

Le fait que cette fonction soit unique facilite son utilisation dans des constructions de programmation fonctionnelle comme celle-ci :

Il est toujours important de rendre les « flux de travail standard » aussi simples que possible. Par exemple, pour la manipulation des graphes, nous avons le composant VertexOutComponent depuis la version 8.0 (2010). Il donne une liste des sommets qui peuvent être atteints à partir d’un sommet donné. Et pour certaines choses, c’est exactement ce que l’on veut. Mais parfois, il est beaucoup plus pratique d’obtenir le sous-graphe (et en fait, dans le formalisme de notre projet de physique, ce sous-graphe – que nous considérons comme une « boule géodésique » – est une construction assez centrale). Dans la version 12.3, nous avons donc ajouté VertexOutComponentGraph :

Un autre exemple d’une petite « amélioration du flux de travail » se trouve dans HighlightImage. HighlightImage prend généralement une liste de régions d’intérêt à mettre en évidence dans l’image. Mais des fonctions comme MorphologicalComponents ne se contentent pas de dresser des listes de régions dans une image ; elles produisent plutôt une « matrice d’étiquetage » qui place des nombres pour étiqueter les différentes régions d’une image. Ainsi, pour rendre le flux de travail de HighlightImage plus fluide, dans la version 12.3, nous l’avons laissé utiliser directement une matrice d’étiquettes, en assignant des couleurs différentes aux régions étiquetées différemment :

Nous nous efforçons de garantir la cohérence et l’interopérabilité du langage Wolfram. (Et en fait, nous avons toute une initiative autour de cela que nous appelons « Language Completeness & Consistency », dont nous livestreamons régulièrement les réunions hebdomadaires). L’une des diverses facettes de l’interopérabilité est que nous voulons que les fonctions soient capables de « manger » toute entrée raisonnable et de la transformer en quelque chose qu’elles peuvent « naturellement » gérer.

Et comme petit exemple de ceci, quelque chose que nous avons ajouté dans la version 12.3 est la conversion automatique entre les espaces de couleur. Rouge signifie par défaut la couleur RGB rouge (RGBColor[1,0,0]). Mais maintenant

signifie transformer ce rouge en rouge dans l’espace de teinte :

Disons que vous effectuez un long calcul. Vous voulez souvent avoir une indication de la progression qui est faite. Dans la version 6.0 (2007) nous avons ajouté Monitor, et dans les versions suivantes nous avons ajouté un rapport de progression automatique intégré pour certaines fonctions, par exemple NetTrain. Mais nous avons maintenant une initiative en cours pour ajouter systématiquement des rapports de progression pour toutes sortes de fonctions qui peuvent finir par faire de longs calculs. ($ProgressReporting = False le désactive globalement).

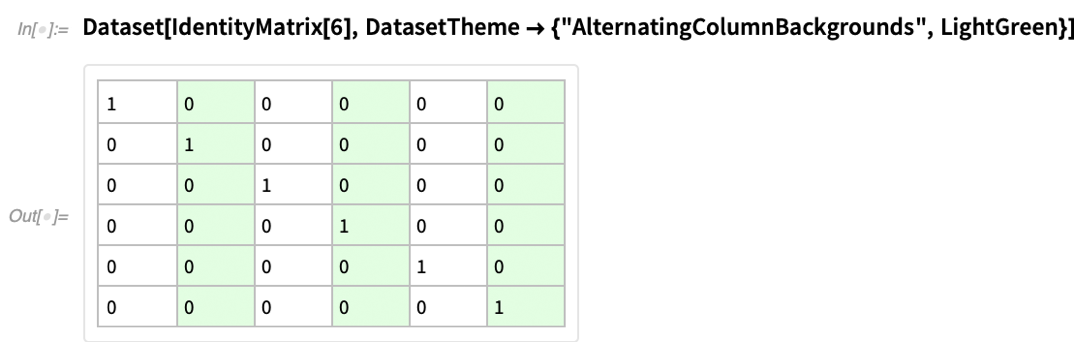
Nous travaillons dur dans Wolfram Language pour nous assurer que nous choisissons de bonnes valeurs par défaut, par exemple pour la façon d’afficher les choses. Mais parfois, vous devez indiquer au système le type de « look » que vous souhaitez. Dans la version 12.3, nous avons ajouté l’option DatasetTheme pour spécifier des « thèmes » pour l’affichage des objets Dataset.

Au fond, chaque thème ne fait que définir des options spécifiques, que vous pourriez définir vous-même. Mais le thème est un « changement de banque » d’options d’une manière pratique. Voici un ensemble de données de base avec un formatage par défaut :

Le voici plus « vivant » pour le web :

Vous pouvez également donner diverses « directives de thème » :

Ainsi que des conseils supplémentaires :

Je ne sais pas trop pourquoi nous n’y avons pas pensé avant, mais dans la version 11.3 (2018), nous avons introduit une très belle » innovation d’interface utilisateur » : Iconize. Et dans la version 12.3, nous avons ajouté un autre élément de polissage à l’iconisation. Si vous sélectionnez une partie d’une expression, puis utilisez Iconize dans le menu contextuel (« clic droit »), une sous-partie appropriée de l’expression sera iconisée, même si la sélection que vous avez faite peut avoir inclus une virgule supplémentaire, ou être quelque chose qui ne peut pas être une sous-partie stricte de l’expression :

Imaginons que vous génériez un objet dont le stockage nécessite beaucoup de mémoire :

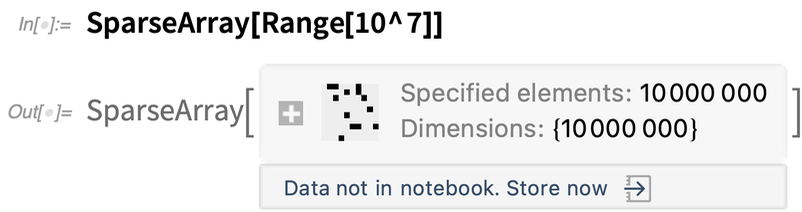Par défaut, l’objet est conservé dans votre session du noyau, mais il n’est pas stocké directement dans votre ordinateur portable – il ne persistera donc pas après la fin de votre session actuelle du noyau. Dans la version 12.3, nous avons ajouté quelques options concernant l’endroit où vous pouvez stocker les données :

L’importation et l’exportation de données constituent un domaine important dans lequel nous nous efforçons de faire en sorte que les choses « fonctionnent ». Le langage Wolfram prend désormais en charge environ 250 formats de données externes, avec par exemple de nouveaux formats de données statistiques comme SAS7BDAT, DTA, POR et SAV ajoutés dans la version 12.3.

Beaucoup de choses sont devenues plus rapides

En plus de tous les efforts que nous déployons pour créer de nouvelles fonctionnalités pour Wolfram Language, nous essayons toujours d’améliorer et d’accélérer les fonctionnalités existantes. Dans la version 12.3, de nombreux éléments sont désormais plus rapides. Un groupe particulièrement important de choses est devenu plus rapide grâce aux progrès de notre technologie de compilation technologie de compilation qui permet de compiler un plus grand nombre de fonctionnalités de Wolfram Language directement en code machine optimisé. Around est un exemple de bénéficiaire de cette technologie.

Voici un calcul effectué avec Around:

Dans la version 12.2, faire cette opération 10 000 fois prend environ 1,3 seconde sur mon ordinateur :

Dans la version 12.3, il est environ 100 fois plus rapide :

Il y a beaucoup de raisons différentes pour lesquelles les choses sont devenues plus rapides dans la version 12.3. Dans le cas de Permanent, par exemple, nous avons pu utiliser un nouvel algorithme bien meilleur. Le voici dans la version 12.2 :

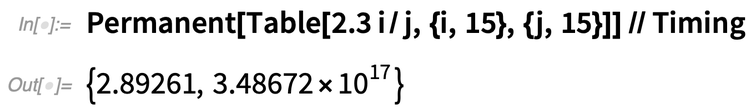Et maintenant dans la 12.3 :

Un autre exemple est l’analyse des dates : la conversion des dates d’un texte à une forme interne. La principale avancée dans ce domaine est venue du fait que l’analyse des dates est souvent effectuée en masse, et qu’il est donc logique de mettre en cache de manière adaptative certaines parties de l’opération. Et le résultat, par exemple lors de l’analyse d’un million de dates, est que ce qui prenait plusieurs minutes ne prend plus que quelques secondes.

Un autre exemple est celui de Rasterize, qui dans la version 12.3 est généralement 2 à 4 fois plus rapide que dans la version 12.2. La raison de cette accélération est quelque peu subtile. Lorsque Rasterize a été introduit pour la première fois dans la version 6.0 (2007) , la vitesse de transfert des données entre les processus était un problème, et il était donc judicieux de compresser les données transférées. Mais aujourd’hui, les vitesses de transfert sont beaucoup plus élevées et nous disposons de structures de données de tableaux mieux optimisées. La compression n’a donc plus de sens et sa suppression (associée à d’autres optimisations du chemin de code) permet à Rasterize d’être beaucoup plus rapide.

Une avancée importante de la version 12.1 a été l’introduction de DataStructure, permettant l’utilisation directe de structures de données d’optimisation (mises en œuvre par notre nouvelle technologie de compilation). La version 12.3 introduit plusieurs nouvelles structures de données. Il y a « ByteTrie » pour les recherches rapides basées sur les préfixes (pensez à Autocomplete et GenomeLookup), et il y a « KDTree » pour les recherches géométriques rapides (pensez à Nearest). Il y a aussi maintenant « ImmutableVector« , qui est fondamentalement comme une liste ordinaire du Wolfram Language, sauf qu’elle est optimisée pour un ajout rapide.

En plus des améliorations de vitesse dans le noyau de calcul, la version 12.3 a également amélioré la vitesse de l’interface utilisateur. On notera en particulier une accélération significative du rendu sur les plates-formes Windows, obtenue en utilisant DirectWrite et en exploitant les capacités du GPU.

Repousser la frontière des mathématiques

La version 1 de Mathematica a été présentée comme « un système permettant de faire des mathématiques par ordinateur”, et, depuis plus de trente ans, chaque nouvelle version de Wolfram Language et de Mathematica a apporté des innovations dans le domaine des « mathématiques par ordinateur ».

Pour la version 12.3, parlons d’abord de la résolution d’équations symboliques. Dès laversion 3 (1996) nous avons introduit l’idée de représentations implicites des « objets Root » pour les racines des polynômes, ce qui nous a permis d’effectuer des calculs symboliques exacts même sans « formules explicites » en termes de radicaux. La version 7 (2008) a ensuite généralisé Root pour qu’il fonctionne également pour les équations transcendantales.

Qu’en est-il des systèmes d’équations ? Pour les polynômes, la théorie de l’élimination signifie que les systèmes ne sont pas vraiment différents des équations individuelles ; les mêmes objets Rootpeuvent être utilisés. Mais pour les équations transcendantes, ce n’est plus vrai. Mais pour la version 12.3, nous avons maintenant trouvé comment généraliser les objets Root afin qu’ils puissent fonctionner avec des racines transcendantales multivariées :

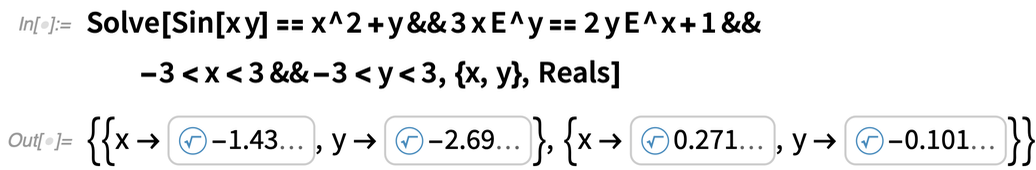Et comme ces objets Root sont exacts, ils peuvent par exemple être évalués avec une précision quelconque :

Dans la version 12.3, il y a également de nouvelles équations, impliquant des fonctions elliptiques, pour lesquelles des résultats symboliques exacts peuvent être donnés, même sans objets Root :

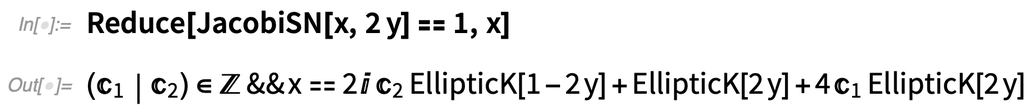Une avancée majeure de la version 12.3 est la possibilité de résoudre symboliquement tout système linéaire d’ODE (équations différentielles ordinaires) avec des coefficients de fonctions rationnelles.

Parfois, le résultat implique des fonctions mathématiques explicites :

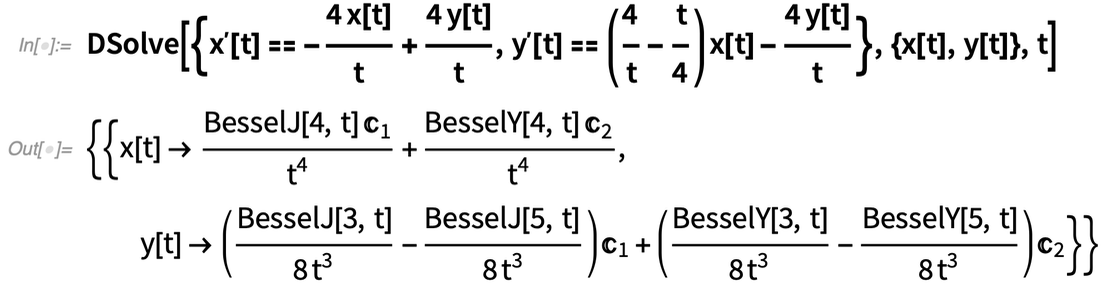Parfois, il y a des intégrales – ou des racines différentielles – dans les résultats :

Une autre avancée de la version 12.3 est la couverture complète des ODE linéaires avec q coefficients de fonctions rationnelles, dans lesquelles les variables peuvent apparaître explicitement ou implicitement dans les exposants. Les résultats sont exacts, bien qu’ils impliquent généralement des racines différentielles :

Qu’en est-il des EDP ? Dans la version 12.2, nous avons introduit un nouveau cadre majeur pour la modélisation avec des EDP numériques. Et maintenant, dans la version 12.3, nous avons produit une monographie complète de 105 pages sur les solutions symboliques aux EDP :

Voici une équation qui, dans la version 12.2, pouvait être résolue numériquement :

Maintenant, il peut être résolu exactement et symboliquement aussi :

En plus des EDP linéaires, la version 12.3 étend la couverture des solutions spéciales aux EDP non linéaires. En voici une (avec 4 variables) qui utilise la méthode de Jacobi :

Un élément ajouté dans la version 12.3, qui prend en charge les EDP et offre une nouvelle fonctionnalité pour le traitement du signal, est la transformée de Laplace bilatérale (c’est-à-dire l’intégration de -∞ à +∞, comme une transformée de Fourier) :

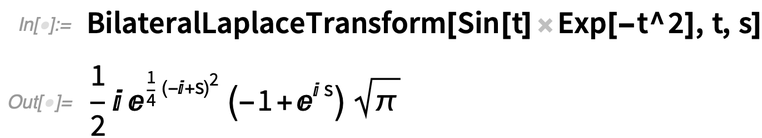Depuis la version 1, nous sommes fiers de notre couverture des fonctions spéciales. Au fil des ans, nous avons pu étendre progressivement cette couverture à des fonctions spéciales de plus en plus générales. La version 12.3 comporte plusieurs nouvelles classes de fonctions spéciales recherchées depuis longtemps. Il y a les intégrales elliptiques de Carlson. Et puis il y a la fonction Fox H.

Dès la version 3 (1996), nous avons introduit MeijerG qui a considérablement élargi la gamme des intégrales définies que nous pouvions faire sous forme symbolique. MeijerG est définie en termes d’intégrale de Mellin-Barnes dans le plan complexe. Il s’agit d’un petit changement dans l’intégrande, mais il a fallu 25 ans pour démêler les mathématiques et les algorithmes nécessaires pour nous amener à la version 12.3 de FoxH.

FoxH est une fonction très générale – qui englobe toutes les fonctions hypergéométriques pFq et Meijer G et bien au-delà. Et maintenant que FoxH est dans notre langage, nous sommes en mesure de commencer le processus d’expansion de notre intégration et d’autres capacités symboliques pour l’utiliser.

Percée de l’optimisation symbolique

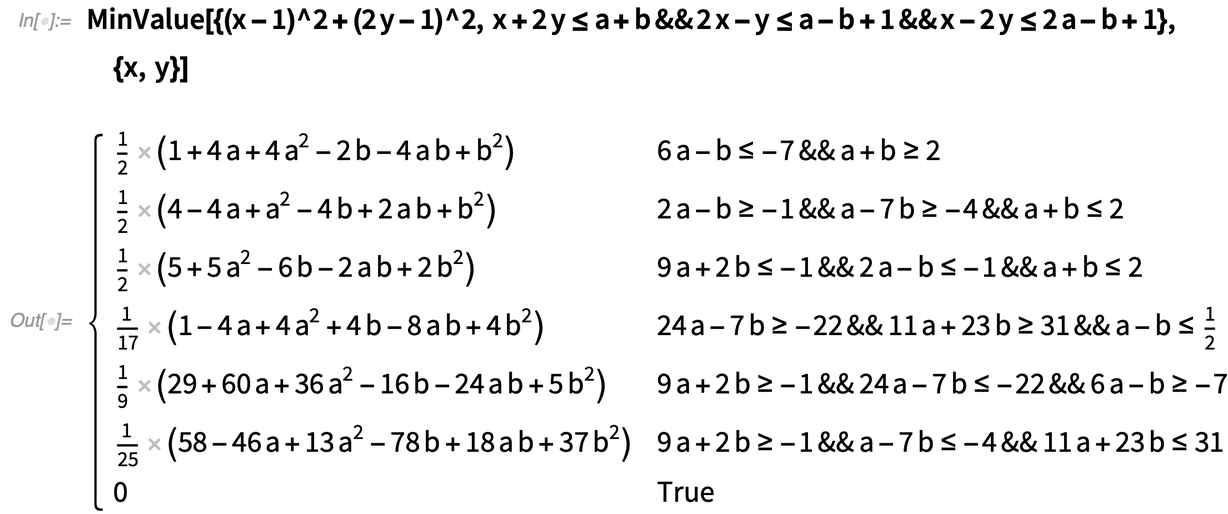Une avancée majeure de la version 12.0 a été l’introduction de l’optimisation convexe à l’échelle industrielle, permettant de traiter couramment des problèmes impliquant des millions de variables dans le cas linéaire et des milliers dans le cas non linéaire. Dans la version 12.0, tout devait être numérique (dans la version 12.1, nous avons ajouté l’optimisation en nombres entiers). Dans la version 12.3, nous ajoutons maintenant la possibilité de paramètres symboliques dans les problèmes linéaires et quadratiques à grande échelle, comme dans ce petit exemple :

Dans les calculs d’optimisation convexe typiques n’impliquant pas de paramètres symboliques, on ne vise que des résultats numériques approximatifs, et il n’était pas clair s’il existait une méthode générale pour obtenir des résultats numériques exacts. Mais pour la version 12.3, nous en avons trouvé une, et nous sommes maintenant capables de donner des résultats numériques exacts que vous pouvez, par exemple, évaluer avec la précision que vous voulez.

Voici un problème d’optimisation géométrique, qui peut maintenant être résolu exactement en termes d’objets de racines transcendantes :

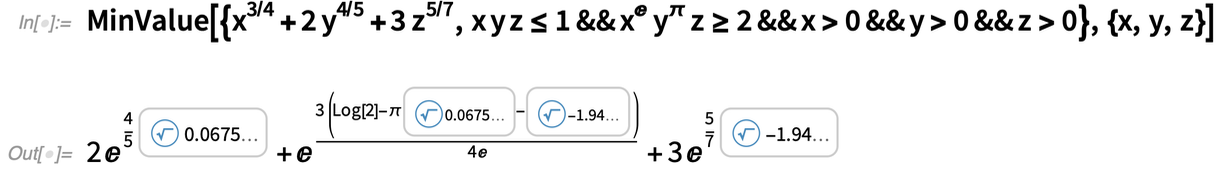Étant donné une telle solution exacte, il est maintenant possible de faire une évaluation numérique avec n’importe quelle précision :

Plus avec les graphiques

Au cas où l’on aurait douté de l’importance des graphes, notre Wolfram Physics Project a montré assez clairement au cours de l’année écoulée qu’au niveau le plus bas, la physique est une question de graphes. En fait, l’ensemble de notre projet de physique a été rendu possible grâce à la riche fonctionnalité des graphiques dans le langage Wolfram.

Dans la version 12.3, nous avons continué à développer cette fonctionnalité. Voici, par exemple, une nouvelle fonction de visualisation 3D pour les graphiques :

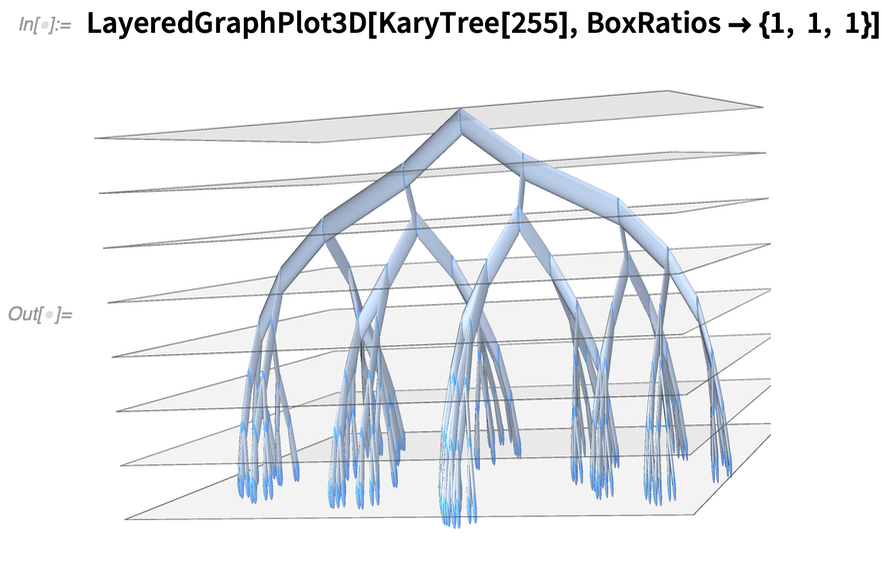Et voici une nouvelle intégration de graphique 3D :

Nous sommes en mesure de trouver des arbres spanning dans les graphes depuis la version 10 (2014). Dans la version 12.3, cependant, nous avons généralisé FindSpanningTree pour traiter directement les objets — comme les emplacements géographiques — qui ont des coordonnées. Voici un arbre spanning basé sur les positions des capitales européennes :

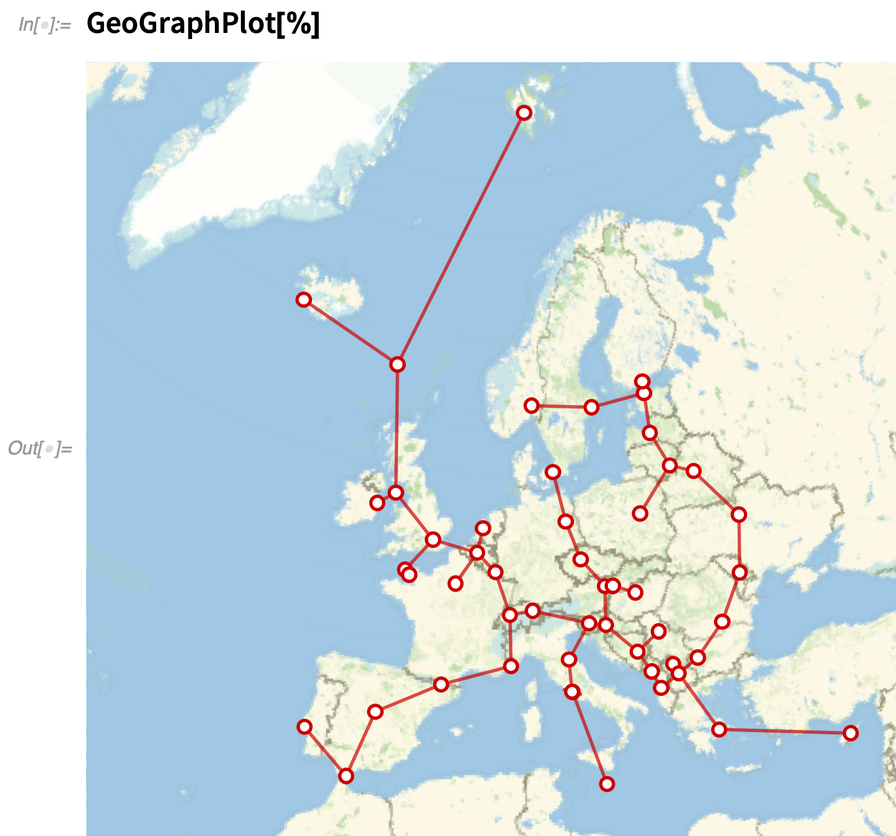Et maintenant, dans la version 12.3, nous pouvons utiliser le nouveau GeoGraphPlot pour le tracer sur une carte :

À propos, dans un « graphe géographique », il existe des moyens « géographiques » d’acheminer les arêtes. Par exemple, vous pouvez spécifier qu’ils suivent (lorsque c’est possible) les indications de conduite (telles que fournies par TravelDirections) :

Euclide rencontre Descartes, et plus encore

Nous avons fait beaucoup de choses avec la géométrie au cours des dernières années, et il y en a encore plus à venir. Dans la version 12.0, nous avons introduit la géométrie synthétique « à la Euclide ». Dans la version 12.3, nous nous connectons à la géométrie analytique » à la Descartes « , en convertissant les descriptions géométriques en formules algébriques.

Étant donné trois points symboliquement spécifiés, GeometricTest peut donner la condition algébrique pour qu’ils soient colinéaires :

Pour le cas particulier de la colinéarité, il existe une fonction spécifique pour effectuer le test :

Mais GeometricTest est beaucoup plus général dans sa portée – il supporte plus de 30 types de prédicats. On obtient ainsi la condition pour qu’un polygone soit convexe :

Et cela donne la condition pour qu’un polygone soit régulier :

Et voici la condition pour que trois cercles soient mutuellement tangents (et, oui, ce ∃ est un peu « post Descartes ») :

La version 12.3 apporte également des améliorations à la géométrie de calcul de base. Les plus notables sont RegionDilation et RegionErosion, qui font essentiellement convoler les régions entre elles. RegionDilation trouve effectivement la « région d’union » entière (« somme de Minkowski ») obtenue en traduisant une région en chaque point d’une autre région.

En quoi cela est-il utile ? Il s’avère qu’il y a de nombreuses raisons. L’un des exemples est le “problème du pianiste” (alias le problème de la planification du mouvement des robots). Étant donné, par exemple, une forme rectangulaire, existe-t-il un moyen de la manœuvrer (dans le cas le plus simple, sans rotation) dans une maison comportant certains obstacles (comme des murs) ?

En gros, ce qu’il faut faire, c’est prendre la forme rectangulaire et « dilater la pièce » (et les obstacles) avec elle :

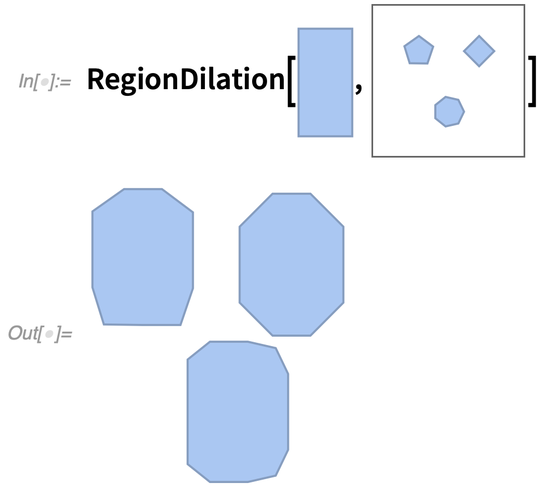Ensuite, s’il reste un chemin connecté d’un point à un autre, il est possible de déplacer le piano le long de ce chemin. (Et bien sûr, le même genre de chose peut être fait pour les robots dans une usine, etc. etc.)

RegionDilation est également utile pour « lisser » ou « décaler » des formes, par exemple pour des applications de CAO :

Au moins dans les cas simples, on peut « faire du Descartes » avec elle et obtenir des formules explicites :

Et, soit dit en passant, tout cela fonctionne dans n’importe quel nombre de dimensions, ce qui constitue un moyen utile de générer toutes sortes de « nouvelles formes » (comme un cylindre est la dilatation d’un disque par une ligne en 3D).

Encore plus de visualisation

Le langage Wolfram dispose d’une vaste collection de fonctions de visualisation intégrées, mais il semble qu’il y en ait toujours plus à ajouter. Nous disposons de ListPlot3D depuis la version 1.0 (1988) ; nous avons ajouté ListPointPlot3D dans la version 6.0 (2007) – et maintenant, dans la version 12.3, nous ajoutons ListLinePlot3D.

Voici une marche aléatoire en 3D rendue avec ListLinePlot3D:

Si vous fournissez plusieurs listes de données, ListLinePlot3D les trace séparément :

Nous avons introduit le traçage de champs vectoriels dans la version 7.0 (2008), avec des fonctions comme VectorPlot et StreamPlot — qui ont été considérablement améliorées dans les versions 12.1 et 12.2. Dans la version 12.3, nous ajoutons maintenant StreamPlot3D (ainsi que ListStreamPlot3D). Voici un tracé de lignes de courant pour un champ vectoriel 3D, coloré en fonction de l’intensité du champ :

C’est une chose de créer un graphique, c’en est une autre de lui donner des axes. Il y a une quantité remarquable de subtilité dans la spécification de la façon dont les axes – et leurs tics et étiquettes – doivent être dessinés. Cela va être une histoire plus longue, mais dans la version 12.3, nous avons les débuts des spécifications symboliques des axes.

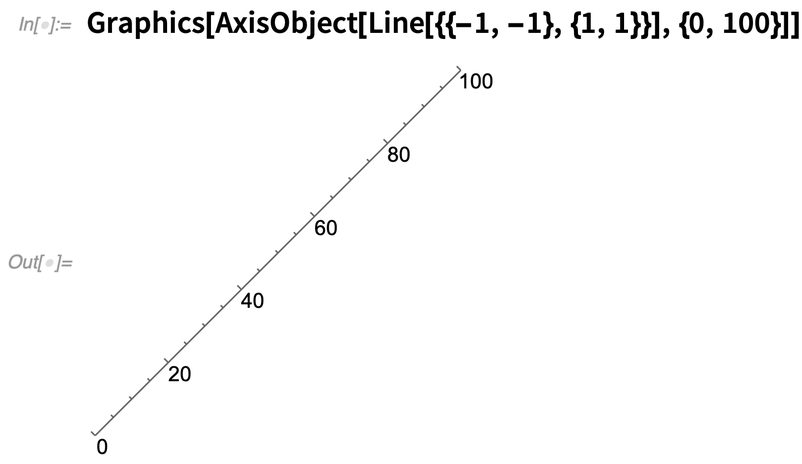
Les axes fonctionnent un peu comme les flèches : vous donnez d’abord la « structure de base », puis vous dites comment l’annoter. Voici un axe qui est étiqueté linéairement de 0 à 100 sur une ligne :

Et voici un axe en spirale (alias étiquetage sur une courbe paramétrique) :

Et, oui, cela fonctionne aussi dans les cas plus ornés :

Parmi les nombreux problèmes subtils, il y a la question de l’orientation des étiquettes des tics par rapport à l’axe :

En parlant de subtilités graphiques, en voici une autre qui est traitée dans la version 12.3. Disons que vous créez une ligne en pointillés :

Les chiffres à l’intérieur de Dashing indiquent la longueur de chaque tiret, et entre les tirets. Dans la version 12.3, vous pouvez indiquer un nombre supplémentaire : le décalage du début du premier tiret :

De plus, vous pouvez contrôler les « bouchons » de chaque tableau de bord, en les arrondissant :

Tous ces détails peuvent sembler infimes, mais ils sont importants pour que les graphiques du langage Wolfram aient une très belle apparence. Par exemple, si vous avez deux axes en pointillés qui se croisent, vous voulez probablement que les « pointillés » soient alignés :

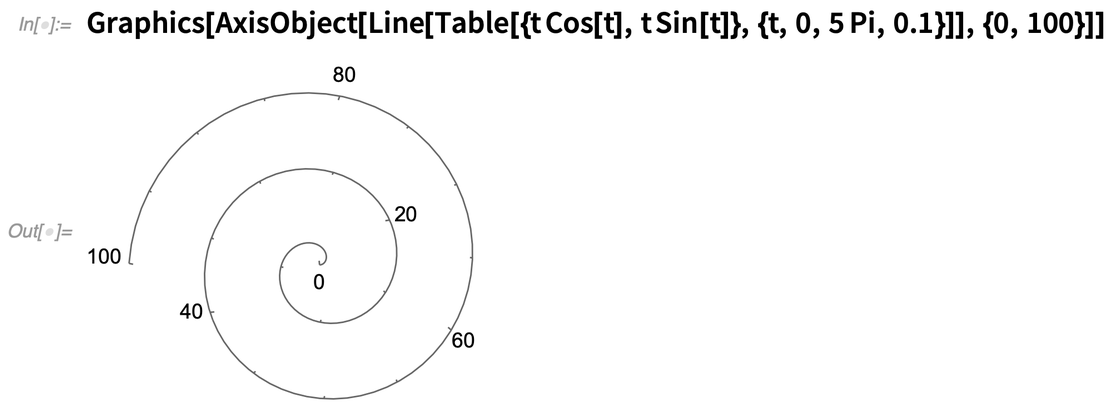
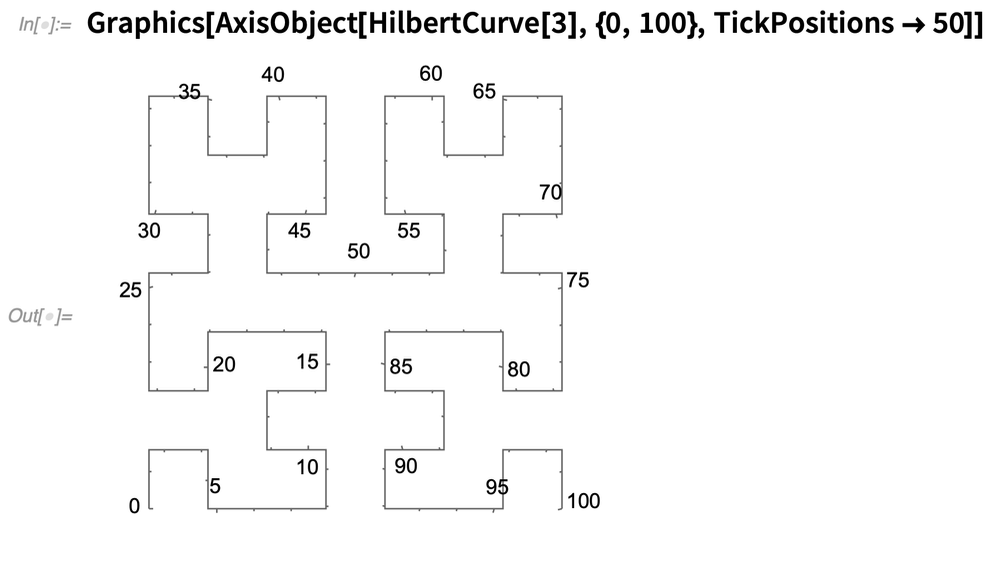
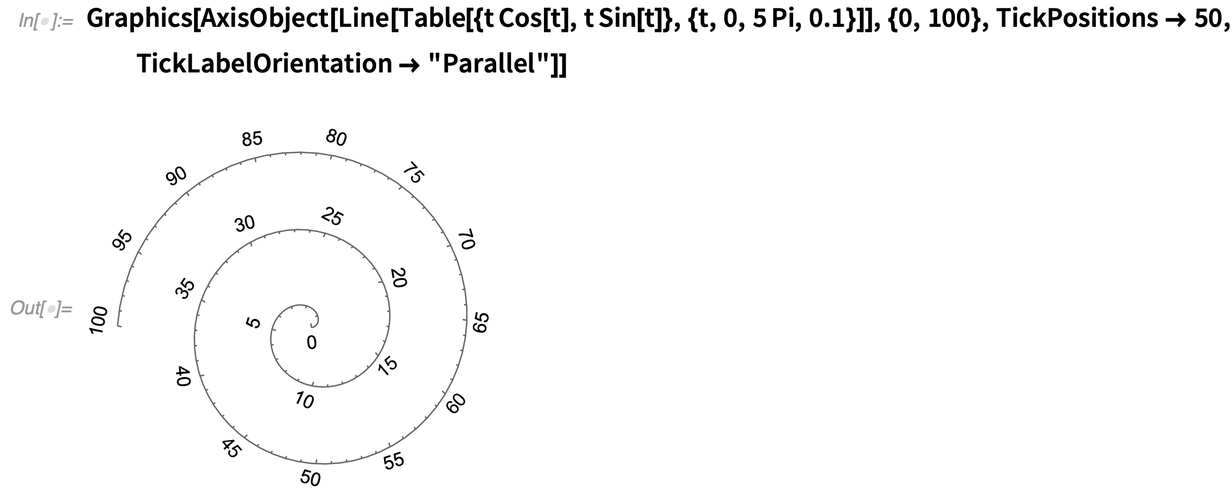
Noeuds d’or, et autres questions matérielles

Nous en parlons presque depuis la version 1.0. Et maintenant, dans la version 12.3, il est enfin là ! Rendu réaliste des surfaces en tant que matériaux. Voici un nœud, rendu comme s’il était fait d’or :

Voici une surface, en velours :

Dans la version 12.3, nous prenons en charge un peu plus d’une douzaine de matériaux standard nommés (et d’autres à venir). Mais MaterialShading est également configuré pour vous permettre de spécifier en détail les propriétés physiques et géométriques explicites des matériaux, de sorte que vous pouvez obtenir des effets comme celui-ci :

Remarquez, au passage, le nouveau paramètre « ThreePoint » pour Lighting — essentiellement une simulation d’un placement standard des lumières dans un studio de photographie.

La modélisation de l’interaction de la lumière avec les surfaces – et le « rendu basé sur la physique » – est un sujet complexe, qui fait l’objet d’une monographie complète dans la version 12.3 :

Arbres!

Si l’on se base sur le nombre de nouvelles fonctions intégrées, le vainqueur incontestable du plus grand nouveau cadre de la version 12.3 est celui des arbres. Depuis plus de dix ans, nous sommes en mesure de traiter les arbres comme un cas particulier de graphes (et bien sûr, toutes les expressions symboliques dans le Wolfram Language sont finalement représentées comme des arbres). Mais dans la version 12.3, nous introduisons les arbres comme objets de première classe dans le système.

L’objet fondamental est Tree:

Tree prend deux arguments : une « charge utile » (qui peut être n’importe quelle expression), et une liste de sous-arbres (et, oui, les arbres sont par défaut rendus légèrement verts, en clin d’œil à leurs analogues botaniques).

Il existe une variété de fonctions « *Tree » pour construire des arbres, et des fonctions « Tree* » pour convertir les arbres en d’autres choses. RulesTree, par exemple, construit un arbre à partir d’une collection imbriquée de règles :

Et TreeRules va dans l’autre sens, en convertissant un arbre en une collection imbriquée de règles :

ExpressionTree crée un arbre à partir de la structure d’une expression :

Dans un sens, il s’agit d’une représentation directe d’une expression FullForm expression, comme le montre, par exemple, TreeForm. Mais il existe également des moyens de transformer une expression en arbre. Ainsi, les nœuds de l’arbre contiennent des sous-expressions complètes, de sorte que les expressions à un niveau donné de l’arbre sont essentiellement ce qu’une fonction comme Map considérerait comme les expressions à ce niveau (avec Heads → True) :

Voici une autre version, qui supprime effectivement la redondance des sous-expressions imbriquées et traite les têtes d’expression comme les autres parties (dans le « style S-expression ») :

Pourquoi avons-nous besoin Tree alors que nous avons des Graph ? La réponse est qu’il existe plusieurs caractéristiques spéciales des arbres qui sont importantes. Dans un Graph, par exemple, chaque nœud a un nom, et les noms doivent être uniques. Dans un arbre, les nœuds n’ont pas besoin d’être nommés, mais ils peuvent avoir des « charges utiles » qui ne doivent pas être uniques. En outre, dans un graphe, les arêtes d’un nœud donné n’apparaissent pas dans un ordre particulier ; dans un arbre, c’est le cas. Enfin, un arbre possède un nœud racine spécifique, ce qui n’est pas forcément le cas d’un graphe.

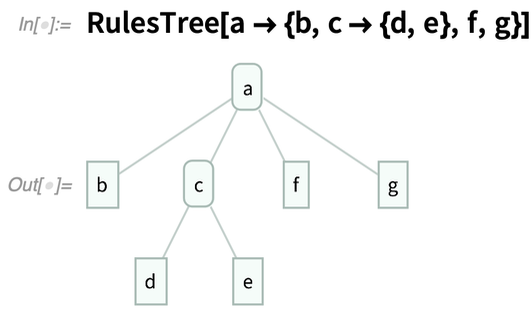
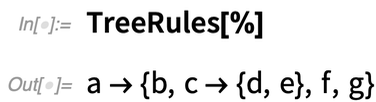
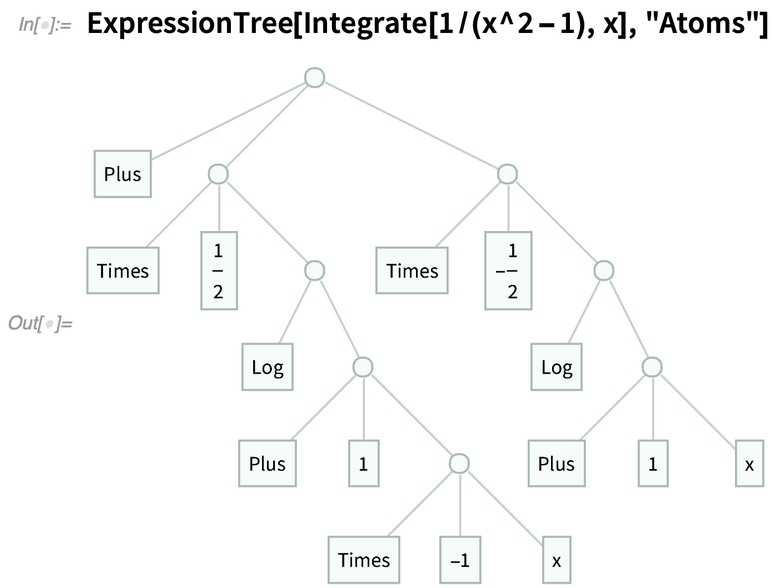
Lors de la conception de Tree nous avons d’abord pensé que nous devrions avoir des représentations symboliques distinctes pour les arbres entiers, les sous-arbres et les nœuds des feuilles. Mais il s’est avéré que nous étions en mesure de réaliser un design élégant avec Tree seul. Les nœuds d’un arbre ont généralement la forme Tree[payload, {child1, child2, …}] où les childi sont des sous-arbres. Un nœud ne doit pas nécessairement avoir une charge utile, auquel cas il peut simplement être donné sous la forme Tree[{child1, child2, …}]. Un nœud feuille est alors Tree[expr, None] ou Tree[None].

Une caractéristique très intéressante de cette conception est que les arbres peuvent immédiatement être construits à partir de sous-arbres, simplement en imbriquant des expressions :

Au fait, nous pouvons transformer cet objet en un objet Graph générique avec TreeGraph:

Remarquez que, comme Graph ne fait pas attention à l’ordre des nœuds, certains nœuds ont été inversés dans ce rendu. Il a également fallu donner des noms distincts aux nœuds afin de préserver l’arborescence :

S’il existe un graphe générique qui se trouve être un arbre, GraphTree le convertit en forme explicite Tree :

RandomTree produit un arbre aléatoire d’une taille donnée :

On peut également créer des arbres à partir de fonctions imbriquées : NestTree produit un arbre en générant de manière imbriquée les charges utiles des nœuds enfants à partir des charges utiles des nœuds parents :

OK, donc, étant donné un arbre, que pouvons-nous en faire ? Il existe une variété de fonctions d’arbre qui sont des analogues directs des fonctions pour les expressions génériques. Par exemple, TreeDepth donne la profondeur d’un arbre :

TreeLevel est directement analogue à Level. Ici, nous obtenons des sous-arbres qui commencent au niveau 2 de l’arbre :

Comment obtenir un sous-arbre particulier d’un arbre donné ? Fondamentalement, il a une position, tout comme une sous-expression aurait une position dans une expression ordinaire :

TreeSelect vous permet de sélectionner des sous-arbres dans un arbre donné :

TreeData sélectionne les charges utiles, par défaut pour les racines des arbres (TreeChildren sélectionne les sous-arbres) :

Il existe également des TreeCases, TreeCount et TreePosition — qui recherchent par défaut les sous-arbres dont les charges utiles correspondent à un motif spécifié. One can do functional programming with trees just like with generic expressions. TreeMap fait correspondre une fonction sur (les charges utiles dans) un arbre :

TreeFold effectue une opération légèrement plus compliquée. Ici, f « accumule effectivement des données » en balayant l’arbre, g étant appliqué à la charge utile de chaque feuille (pour « initialiser l’accumulation ») :

Il y a beaucoup de choses qui peuvent être représentées par des arbres. Les arbres généalogiques en sont un exemple classique. Voici un cas où il existe des données intégrées que nous pouvons utiliser :

Cela permet de construire un arbre généalogique à deux niveaux :

À propos, notre Tree system est très évolutif et peut aisément gérer des arbres comportant des millions de nœuds. Mais dans la version 12.3, nous n’en sommes qu’au début ; dans les versions suivantes, il y aura toutes sortes d’autres fonctionnalités d’arbres, ainsi que des applications pour analyser les arbres/a>, les arbres XML, etc.

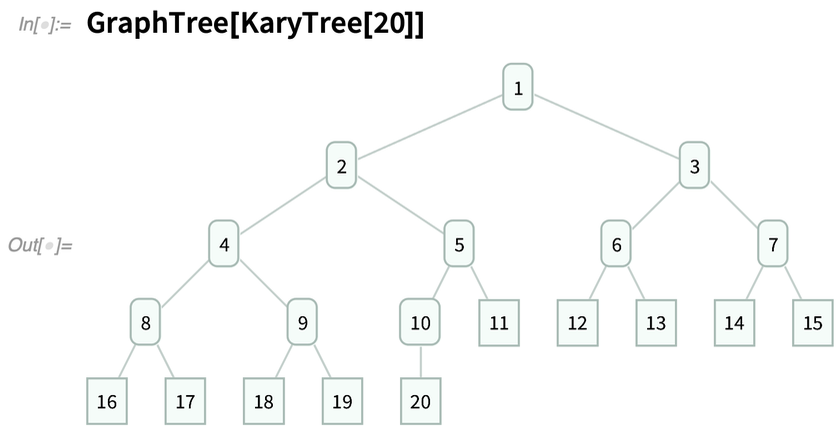
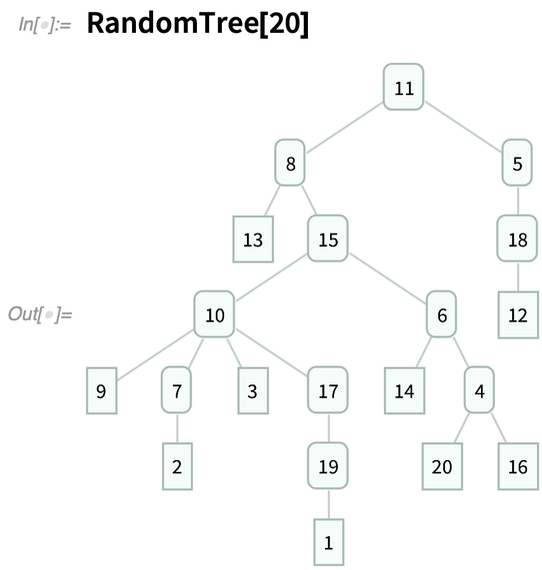
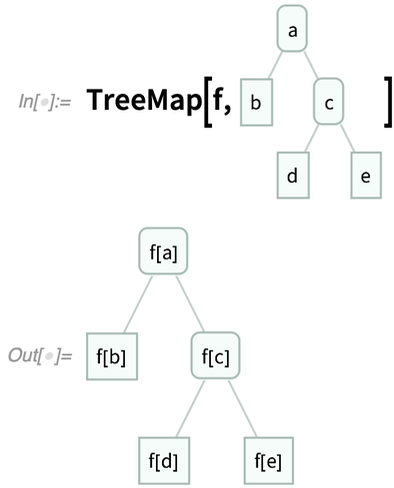
Dates, heures et à quelle vitesse la Terre tourne-t-elle ?

Les dates et les heures sont compliquées. Non seulement il faut tenir compte des différents systèmes de calendrier et des différents fuseaux horaires, mais il existe également des conventions différentes selon les langues et les régions. La version 12.3 ajoute la prise en charge des conventions de date et d’heure pour plus de 700 « locales » différentes.

Voici une date avec les conventions standard utilisées en suédois :

Et cela montre la différence entre les conventions britanniques et américaines, toutes deux pour l’anglais :

Et ceci montre la différence entre les conventions britanniques et américaines, toutes deux pour l’anglais :
Dans la version 12.3, il y a une nouvelle spécification détaillée sur la façon dont les formats de date doivent être construits :

Qu’en est-il dans l’autre sens : d’une chaîne de date à un objet date ? Le nouveau FromDateString permet de le faire :

Au-delà des questions relatives à l’affichage des dates et des heures, il y a aussi la question de la détermination exacte des temps. Depuis les années 1950, il existe une norme de base, le « temps atomique » (lui-même compliqué par les effets relativistes et gravitationnels). Mais avant cela, et encore aujourd’hui pour de nombreuses applications, on souhaite déterminer le temps à partir du Soleil ou des étoiles.

Nous avons introduit le temps sidéral (basé sur les étoiles) dans la version 10.0 (2014) :

Et maintenant, dans la version 12.3, nous ajoutons l’heure solaire, qui est basée sur la position du Soleil dans le ciel :

Cela ne correspond pas tout à fait à l’heure ordinaire, essentiellement en raison de l’heure d’été et de la longitude de l’observateur :

Les choses se compliquent encore plus si l’on veut obtenir des temps précis en astronomie. Et l’un des problèmes majeurs est de connaître l’orientation précise de la Terre. Dans la version 12.3, en préparation d’une couverture plus étendue de l’astronomie, nous avons ajouté GeoOrientationData.

Cette donnée indique la longueur de la journée par rapport à 24 heures :

En 1800, la journée était plus courte :

La pointe de l’apprentissage automatique et des réseaux neuronaux

Nous avons introduit pour la première fois l’apprentissage automatique (avec Predict et Classify) dans la version 10.0 (2014) – et nous avons continué à développer des leading-edge machine learning capabilities depuis lors. La version 12.3 introduit plusieurs nouvelles fonctionnalités très demandées, visant notamment à améliorer l’analyse et le contrôle de l’apprentissage automatique.

Entraînez un prédicteur pour prédire la « qualité du vin » à partir du contenu chimique d’un vin :

Utilisez le prédicteur pour un vin particulier :

Une question courante est alors : « Comment a-t-il obtenu ce résultat ? », ou, plus précisément, « Quelle a été l’importance des différentes caractéristiques du vin pour obtenir ce résultat ? ». Dans la version 12.3, vous pouvez utiliser les valeurs SHAP pour connaître l’importance relative des différentes caractéristiques :

Voici une version visuelle de cette « explication » :

La façon dont les valeurs SHAP sont calculées permet essentiellement de voir dans quelle mesure les résultats changent si différentes caractéristiques des données sont abandonnées. Dans la version 12.3, nous avons ajouté de nouvelles options à des fonctions telles que Predict et Classify afin de contrôler la manière dont les éléments manquants (ou abandonnés) dans les données sont traités à la fois pour l’apprentissage et l’évaluation – ce qui permet de déterminer, par exemple, l’incertitude d’un résultat en raison de données manquantes.

Une question subtile mais importante dans l’apprentissage automatique est le calibrage de la « confiance » des classificateurs. Si un classificateur affirme que certaines images ont 60 % de probabilité d’être des chats, cela signifie-t-il que 60 % d’entre elles sont effectivement des chats ? Un réseau neuronal brut n’y parviendra généralement pas. But one can get closer by recalibrating probabilities using a calibration curve. Dans la version 12.3, en plus du recalibrage automatique, des fonctions comme Classify prennent en charge la nouvelle option RecalibrationFunction qui permet de spécifier la manière dont le recalibrage doit être effectué.

Un élément important de notre cadre d’apprentissage automatique est la prise en charge symbolique approfondie des réseaux neuronaux. Nous avons continué à placer les derniers réseaux neuronaux issus de la littérature de recherche dans notre Neural Net Repository, afin de les rendre immédiatement accessibles dans notre framework à l’aide de NetModel.

Dans la version 12.3, nous avons ajouté quelques fonctionnalités supplémentaires à notre framework, par exemple les fonctions d’activation « swish » et « hardswish » pour ElementwiseLayer. « Il s’est passé beaucoup de choses sous le capot. Nous avons amélioré l’importation et l’exportation ONNX, nous avons considérablement rationalisé l’ingénierie logicielle de notre intégration MXNet, et nous avons presque terminé une version native de notre framework pour Apple Silicon (dans 12.3.0, le framework fonctionne via Rosetta).

Nous essayons toujours de rendre notre cadre d’apprentissage automatique aussi automatisé que possible. Pour y parvenir, il est très important que nous disposions d’un grand nombre d’encodeurs et de décodeurs de réseaux conservés que vous pouvez immédiatement utiliser sur différents types de données. Dans la version 12.3, une extension à cela est l’utilisation d’un extracteur de caractéristiques arbitraire comme codeur net, qui peut être formé dans le cadre de votre processusde formation principal. Pourquoi est-ce important ? Il s’agit d’un moyen entraînable d’alimenter un réseau neuronal avec des collections arbitraires de données de différents types, même s’il n’existe aucun moyen prédéfini de savoir comment les données peuvent être transformées en quelque chose comme un tableau de nombres adapté à l’entrée d’un réseau neuronal.

En plus de fournir un accès direct à l’apprentissage automatique de pointe, le langage Wolfram possède un nombre croissant de fonctions intégrées qui font un usage interne puissant de l’apprentissage automatique. L’une de ces fonctions est TextCases. Dans la version 12.3, TextCases s’est considérablement renforcé, notamment en prenant en charge des types de contenu textuelmoins courants, comme « Protein » et « BoardGame« :

Nouveautés en vidéo

We first introduced video into the Wolfram Language in Version 12.1, and in 12.2 we added many additional video capabilities. In 12.3 we’re adding still more capabilities, with yet more to come.

A major group of new capabilities in 12.3 revolve around programmatic video generation. There are three basic new functions: FrameListVideo, SlideShowVideo and AnimationVideo.

FrameListVideo takes a raw list of images, and assembles a video by treating them as successive raw frames. SlideShowVideo similarly takes a list of images, but now it creates a “slide show video” in which each image is displayed for a specified duration. Here, for example, each image is displayed in the video for 1 second:

SlideShowVideo peut aussi faire des choses comme prendre une TimeSeries dont les valeurs sont des images et la transformer en un diaporama vidéo.

AnimationVideo ne prend pas d’images existantes ; au lieu de cela, il prend une expression et l’évalue ensuite « à la manière d’un Manipulate » pour une gamme de valeurs d’un paramètre. (En fait, il s’agit d’un analogue d’Animatepour la création de vidéos).

Et si vous voulez capturer une vidéo, par exemple à partir d’une caméra ? Un jour, il y aura un moyen interactif de le faire dans un notebook. Mais dans la version 12.3, nous avons ajouté les capacités programmatiques sous-jacentes, et en particulier la fonction VideoRecord. Voici donc un enregistrement de 5 secondes de ma caméra par défaut :

Et voici la vidéo qui en résulte :

Mais VideoRecord peut également utiliser d’autres sources. Par exemple, si vous lui donnez un NotebookObject, il enregistrera ce qui se passe dans ce notebook. Et si vous lui donnez une URL (par exemple pour une webcam), il enregistrera les images qui sont diffusées à partir de cette URL :

Une fonctionnalité très demandée que nous avons ajoutée dans la version 12.3 est la possibilité de combiner des vidéos, par exemple en composant une vidéo dans une autre, ou en assemblant chaque image comme uncollage.

Ainsi, par exemple, voici mon écran vert composté avec le flux ci-dessus :

Notez que pour ce faire, nous utilisons Parallelize — qui fonctionne depuis peu avec VideoFrameMap dans la version 12.3.

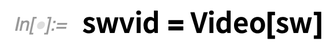
La version 12.3 ajoute également quelques nouvelles fonctionnalités d’édition vidéo. VideoTimeStretch vous permet de « déformer le temps » dans une vidéo selon une fonction spécifiée. VideoInsert vous permet d’insérer un clip vidéo dans une vidéo, et VideoReplace vous permet de remplacer une partie d’une vidéo par une autre.

L’un des avantages de la vidéo dans le Wolfram Language est qu’elle peut être immédiatement analysée à l’aide de tous les outils du langage. Cela inclut l’apprentissage automatique et, dans la version 12.3, nous avons commencé à permettre aux vidéos d’être encodées pour le calcul des réseaux neuronaux. La version 12.3 comprend un simple encodeur de réseau basé sur les images pour les vidéos, ainsi que quelques extracteurs de caractéristiques intégrés. D’autres éléments seront bientôt disponibles, notamment une variété de réseaux de traitement et d’analyse vidéo dans le référentiel Wolfram Neural Net Repository.

Plus dans Chimie

La chimie est un nouveau domaine important pour le Wolfram Language. Dans la version 12.0, nous avons introduit Molecule comme représentation symbolique d’une molécule, et nous avons régulièrement élargi ce qui peut être fait avec elle.

Dans la version 12.3, par exemple, il existe de nouvelles propriétés pour Molecule, comme « TautomerList » (reconfigurations possibles en solution) :

Il existe également des fonctions de commodité comme MoleculeName :

Et, oui, avec MoleculeRecognize, vous pouvez simplement découper un diagramme de structure dans une publication et trouver le nom de la molécule :

Étant donné une collection de molécules, une question que l’on souhaite souvent poser est « Qu’est-ce qu’il y a en commun entre ces molécules ? ». Dans la version 12.3, nous disposons désormais de la fonction MoleculeMaximumCommonSubstructure, qui est l’analogue de LongestCommonSubsequence pour la structure moléculaire :

Voici un schéma de la partie commune :

Et maintenant, avec MoleculeAlign, nous pouvons voir comment les molécules s’alignent réellement en 3D :

Étant donné notre force en chimie et en apprentissage automatique, nous sommes maintenant dans une position intéressante pour réunir ces domaines. Et dans la version 12.3, nous avons les débuts de l’apprentissage automatique chimique intégré. Voici des échantillons de deux classes de produits chimiques :

FeatureSpacePlot dispose désormais d’un extracteur de caractéristiques intégré pour les molécules :

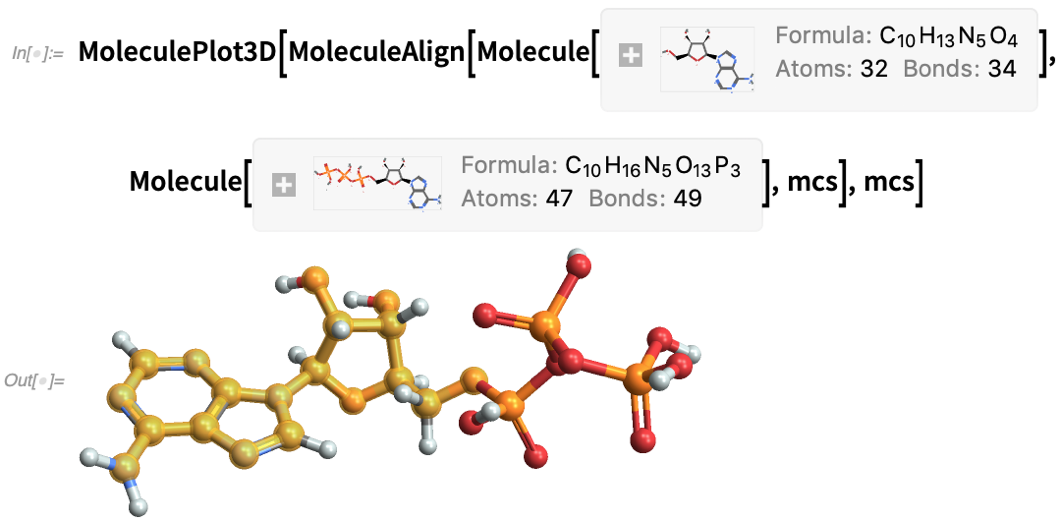
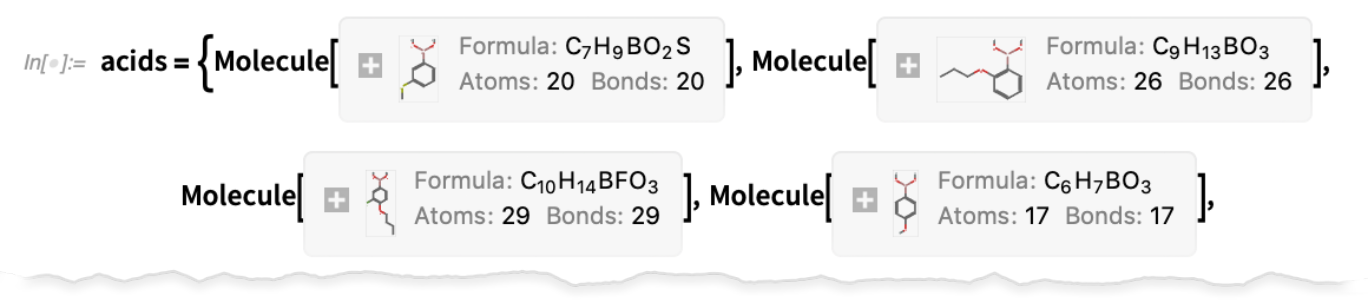
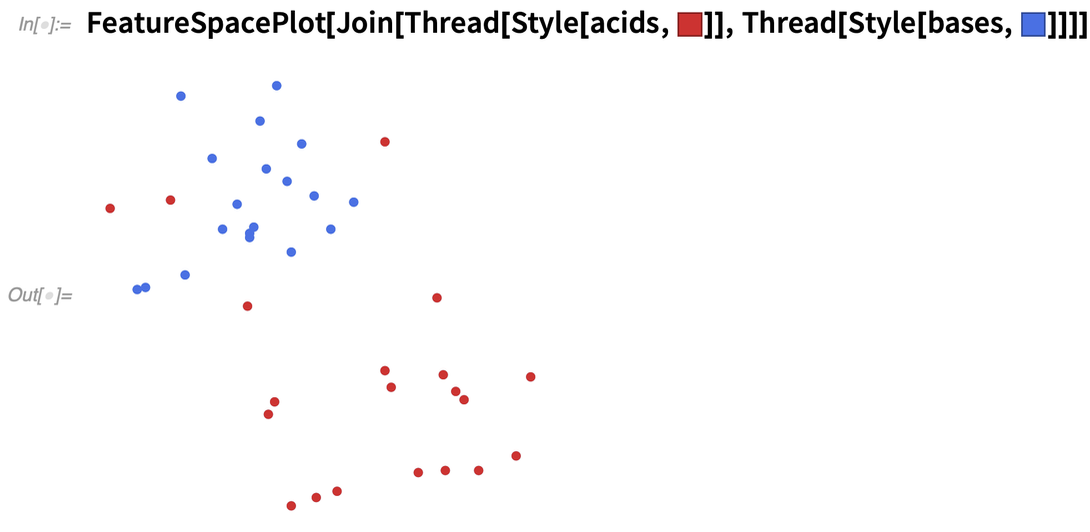
Fermer la boucle pour les systèmes de contrôle

C’est un objectif auquel nous travaillons depuis plus de dix ans. Comment relier nos capacités de représentation et de simulation de systèmes d’ingénierie et autres systèmes à grande échelle à nos capacités en matière de théorie du contrôle ? Ou, en particulier, comment pouvons-nous utiliser nos capacités en matière de systèmes de contrôle pour créer des conceptions pratiques qui peuvent être directement déployées dans les systèmes d’ingénierie ? La version 12.3 prend des mesures importantes pour répondre à cette question et développer ce qui est de plus en plus un flux de travail entièrement automatisé pour la conception de systèmes de contrôle.

Commençons par importer un modèle qui a été créé dans Wolfram System Modeler. Dans ce cas particulier, il s’agit d’un modèle simple pour un sous-marin :

Étant donné le modèle (qui, dans ce cas, consiste en plus de 300 équations différentielles-algébriques), nous pouvons calculer le comportement du système dans différentes situations. Voici par exemple un tracé de la réponse de notre modèle de sous-marin à une force d’impulsion, qui montre essentiellement que la profondeur du sous-marin présente des oscillations amorties :

Mais maintenant la question est : comment pouvons-nous contrôler le sous-marin pour éviter ces oscillations ? En gros, nous voulons mettre en place une boucle fermée dans laquelle un contrôleur prendra le comportement observé du sous-marin et modifiera sa dynamique pour la rendre stable et bien amortie, disons caractérisée par des valeurs propres particulières.

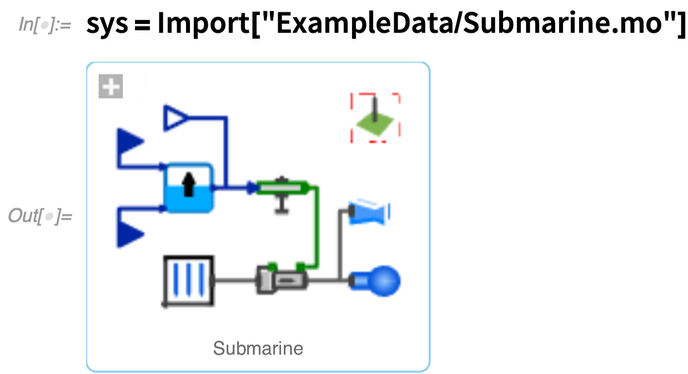
Donc, étant donné le modèle de système sous-jacent, comment pouvons-nous concevoir ce contrôleur ? Eh bien, dans la version 12.3, nous avons réussi à le réduire à quelques fonctions seulement. D’abord, nous donnons le modèle et les paramètres qui vont être contrôlés, et nous spécifions notre objectif de conception en donnant les valeurs propres que nous voulons :

Maintenant, nous pouvons prendre ce contrôleur et le connecter à notre modèle de système :

Comme l’indique le diagramme, il s’agit maintenant d’un système en boucle fermée (le modèle de système original a été effacé dans le cercle gris). Nous pouvons donc maintenant examiner le comportement de ce système en boucle fermée, avec par exemple la même entrée que précédemment :

Maintenant, il n’y a plus d’oscillations ; notre contrôleur a réussi à les amortir et à « rejeter la perturbation ».

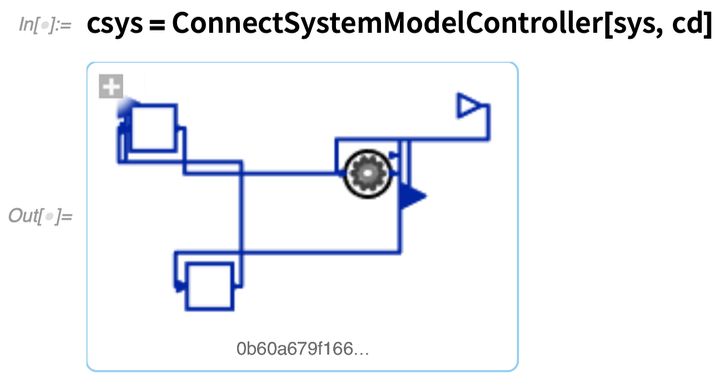
Comment cela a-t-il fonctionné ? Eh bien, comme il est typique dans ce type de conception de systèmes de contrôle, nous avons d’abord trouvé une linéarisation du modèle sous-jacent, appropriée pour le domaine dans lequel nous allions opérer :

Nous pouvons obtenir les valeurs propres de ce modèle linéarisé :

L’objectif du contrôleur est de les déplacer vers l’emplacement souhaité :

Quel est donc le contrôleur qui a été trouvé ? Le voici sous la forme d’un modèle d’espace d’état non linéaire :

Et maintenant il est prêt à être déployé. Et par exemple, nous pouvons compiler le contrôleur pour un Arduino :

Et voici le code source C de l’Arduino :

Inutile de dire que pour un vrai sous-marin, on n’utiliserait pas un Arduino Uno (bien que cela conviendrait probablement très bien pour un sous-marin jouet). Mais l’important ici est que la version 12.3 offre un flux de travail remarquablement automatisé pour passer d’un modèle de système sophistiqué à un système de contrôle.

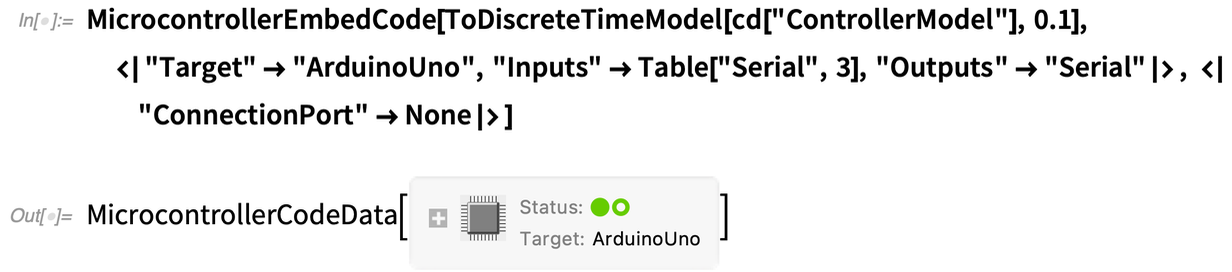
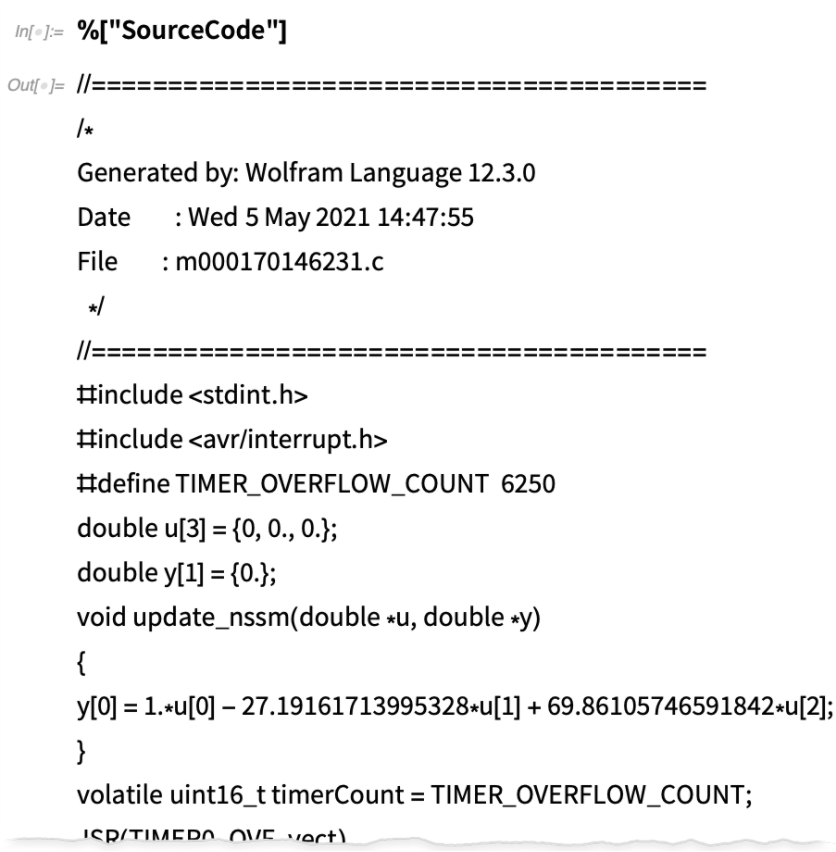
Il va devenir plus facile de taper du code dans les ordinateurs portables

Depuis la version 3.0 (1996), le -> se transforme automatiquement en → lorsque vous saisissez un code. Et nous avons progressivement ajouté des » remplacements automatiques d’entrée » supplémentaires, le plus récent étant la transformation de |-> en ↦ (\[Function]) dans la Version 12.2. Dans la version 12.3, nous généralisons l’ensemble de ce mécanisme (en utilisant la nouvelle option AutoOperatorRenderings), , et nous faisons en sorte que <|.... |> se transforme automatiquement en <| ... |>, et [[ … ]] en 〚 … 〛.

Cela signifie par exemple qu’au lieu que votre code ressemble à ceci

il se transformera immédiatement en cette forme plus lisible dès que vous le taperez :

Il peut sembler étrange qu’il ait fallu autant d’années pour passer de « automatique → » à « automatique 〚〛 ». Mais c’est beaucoup plus subtil que vous ne le pensez, et en fait, cela a nécessité une toute nouvelle approche du rendu de code de type as-you. Dans la version 3.0, l’idée était de remplacer -> par → lorsque vous le tapez. Ainsi, par exemple, si vous effacez ensuite un caractère, vous supprimez l’ensemble du →, plutôt que de simplement » supprimer le > » et de revenir au -.

Mais si vous avez affaire à [[ … ]], vous ne pouvez pas simplement faire ce genre de « remplacement local » sans risque de confusion, certains ]] apparaissant comme 〛 alors que d’autres se séparent en ]] suite à une édition de routine.

Dans la version 12.3, nous ne faisons pas du tout de remplacements, mais nous rendons simplement des séquences de caractères spécifiques (comme ]]) de manière spéciale. Le résultat est que nous pouvons supporter un comportement très général de type « ligature », et que l’espacement arrière inversera toujours exactement les caractères qui ont été saisis.

AutoOperatorRenderings rendra le code que vous tapez plus joli et plus facile à lire. Mais il y a un deuxième changement, plus important, dans la façon dont vous saisissez le code qui est maintenant disponible dans la version 12.3. Il est encore assez expérimental, et n’a donc pas été activé par défaut, mais vous pouvez l’activer explicitement si vous le souhaitez, simplement en évaluant

ou en cochant la case dans l’onglet Interface des Préférences :

L’idée de base – comme le nom DelimiterAutoMatching pourrait le suggérer – est que lorsque vous tapez du code, les délimiteurs que vous saisissez sont automatiquement mis en correspondance, au fur et à mesure que vous tapez.

Cela signifie donc que si vous tapez

ce que vous verrez en réalité est :

En d’autres termes, vous obtiendrez automatiquement les délimiteurs correspondants. (Et par « délimiteurs », nous entendons l’un des éléments suivants : [ …], { … }, ( … ), » … « , [[ … ]], <| ... |> et (* … *).

Qu’advient-il de vos anciennes habitudes de frappe ? Eh bien, vous pouvez toujours les utiliser. Parce que vous pouvez entrer ] pour « taper à travers » la fermeture ]. Et cela signifie que vous tapez exactement les mêmes caractères qu’avant. Mais le point important est que vous n’avez pas besoin de le faire. Le signe ] est déjà là pour vous.

Pourquoi est-ce important ? Essentiellement parce que cela signifie que vous n’avez plus à penser à faire correspondre vos délimiteurs. C’est fait automatiquement pour vous. Depuis la version 3.0 (1996), nous disposons d’une coloration syntaxique qui indique quand les délimiteurs n’ont pas été fermés et qui vous suggère de les fermer. Mais maintenant, la fermeture se fait automatiquement. En particulier, cela signifie que les expressions que vous tapez auront toujours « l’air complet » et ne subiront pas toutes sortes de modifications structurelles au fur et à mesure que vous entrez les caractères.

Inutile de dire que tout cela est beaucoup plus délicat qu’il n’y paraît à première vue. Supposons que vous ayez déjà saisi une expression compliquée et que vous y ajoutiez un délimiteur d’ouverture ou, pire, plusieurs délimiteurs d’ouverture. Où vont les délimiteurs de fermeture ? Quelle part du code déjà présent doit-il contenir ? Parfois, c’est assez évident, mais parfois ça ne l’est pas. Vous pouvez toujours supprimer un délimiteur de fermeture ajouté de manière inappropriée, mais nous travaillons dur pour utiliser l’heuristique appropriée afin d’ajouter le délimiteur de fermeture au bon endroit ou de ne pas l’ajouter du tout.

Qu’est-ce qui ne va pas avec ce code ? Analyse du code et assistance

« Tout automatiser » est un thème important dans ce que nous essayons de réaliser avec le Wolfram Language. Qu’en est-il du débogage ? Peut-on l’automatiser ? Nous y pensons depuis longtemps, et dans la version 12.3 nous avons introduit les premières étapes de notre système d’analyse de code et d’assistance.

Nous avons des choses comme la coloration syntaxique et ^pour les arguments manquants depuis des décennies. Et elles sont extrêmement utiles. Mais ce que nous voulons, c’est quelque chose de plus global. Quelque chose qui ne ressemble pas tant à la correction orthographique qu’à la capacité de dire si un morceau de texte signifie la bonne chose.

On pourrait penser qu’il y a là une sorte de problème philosophique. Dans le langage Wolfram, tout morceau de code – pour autant qu’il soit syntaxiquement correct – est une expression symbolique qui, à un certain niveau, signifie quelque chose. La question est de savoir si ce « quelque chose » est ce que vous voulez. Et le fait est qu’en connaissant la structure typique d’un « code correct », il est souvent possible de faire une très bonne estimation. Et c’est ce que fait notre nouveau système d’analyse de code.

Disons que vous avez ce simple morceau de code :

Dans la version 12.3, il y a un nouvel élément de menu contextuel (« clic droit ») Analyser la cellule. Voici ce qu’il fait :

L’analyse de code a remarqué que les expressions sur les deux branches du If sont les mêmes (comme cela aurait pu arriver si vous les aviez copiées et collées, avec l’intention d’en changer une, mais en oubliant). Ce n’est pas strictement « mauvais » d’avoir les mêmes branches, mais ce n’est presque certainement pas ce que vous vouliez, et si vous aviez toujours voulu donner la même expression, alors votre code serait beaucoup moins obscur si vous donniez simplement l’expression.

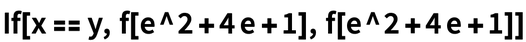
Voici un exemple un peu plus compliqué :

Nous avons cliqué sur la description et obtenu une suggestion sur la façon de corriger les choses, que nous pouvons immédiatement mettre en œuvre en cliquant sur la suggestion. (La boîte d’analyse de code vous donne effectivement un aperçu ; cliquez sur Appliquer les modifications pour changer réellement votre code original).

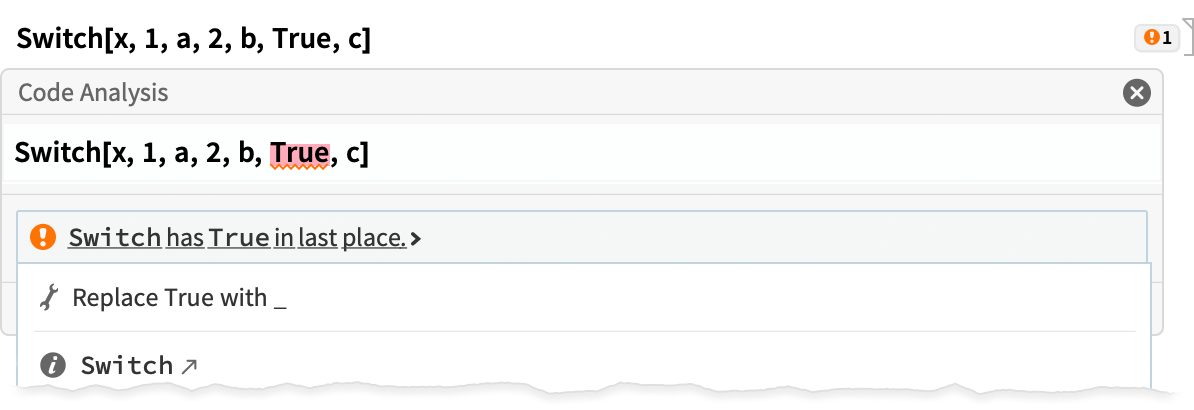
L’analyse de code permet-elle de détecter de véritables erreurs ? Oui, et nous en avons la preuve, car nous l’avons utilisé sur notre code interne, ainsi que sur des exemples dans notre documentation. Par exemple, dans la version 12.2, la documentation de FitRegularization contenait l’exemple suivant :

Lancez l’analyse du code et vous verrez

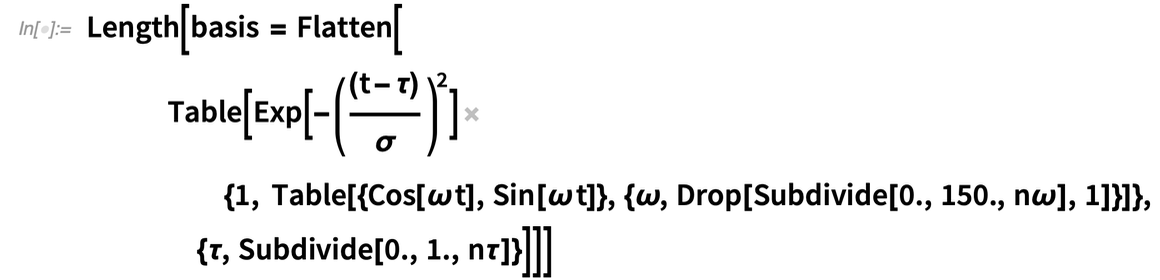
Avancées dans le compilateur : Portabilité et bibliothéconomie

Nous avons un grand projet à long terme de compilation du Wolfram Language directement en code machine efficace. Au fur et à mesure que le projet avance, il devient possible d’effectuer de plus en plus de développements de base en utilisant le compilateur. En outre, dans des éléments tels que le Wolfram Function Repository, de plus en plus de fonctions – ou de fragments de fonctions – sont capables d’utiliser le compilateur.

Dans la version 12.3, nous avons pris une mesure importante pour faciliter le flux de travail dans ce domaine. Imaginons que vous compiliez une fonction très simple :

Quelle est cette sortie ? Eh bien, dans la version 12.3, c’est un objet symbolique qui contient du code brut de bas niveau :

Mais un point important est que tout est là, dans cet objet symbolique. Vous pouvez donc le prendre et l’utiliser :

Il y a cependant un petit problème. Par défaut, FunctionCompile génère du code brut de bas niveau pour le type d’ordinateur sur lequel vous travaillez. Mais si vous transférez la CompiledCodeFunction résultante sur un autre type d’ordinateur, elle ne sera pas en mesure d’utiliser le code de bas niveau. (Il conserve une copie de l’expression originale avant la compilation, de sorte qu’il peut toujours s’exécuter, mais ne bénéficiera pas de l’avantage d’efficacité du code compilé).

Dans la version 12.3, il y a une nouvelle option à FunctionCompile : TargetSystem. Et avec TargetSystem → All, vous pouvez indiquer à FunctionCompile de créer un code de bas niveau à compilation croisée pour tous les systèmes actuels :

Inutile de dire qu’il est plus lent de faire toute cette compilation. Mais le résultat est un objet portable qui contient du code de bas niveau pour toutes les plateformes actuelles :

Ainsi, si vous disposez d’un carnet de notes – ou d’une entrée du Wolfram Function Repository – qui contient ce type de CompiledCodeFunction, vous pouvez l’envoyer à n’importe qui, et elle sera automatiquement exécutée sur son système.

Il existe quelques autres subtilités à ce sujet. Le code de bas niveau créé par défaut dans FunctionCompile est en fait du code LLVM IR (représentation intermédiaire), et non du code machine pur. L’IR LLVM est optimisée pour chaque plate-forme particulière, mais lorsque le code est chargé sur la plate-forme, il y a une petite étape supplémentaire de conversion locale en code machine réel. Vous pouvez utiliser UseEmbeddedLibrary → True pour éviter cette étape, et pré-créer une bibliothèque complète qui inclut votre code.

Cela rendra le chargement du code compilé légèrement plus rapide sur votre plateforme, mais le piège est que la création d’une bibliothèque complète ne peut se faire que sur une plateforme spécifique. Nous avons construit un prototype de système de compilation en tant que service basé sur le cloud, mais nous ne savons pas encore si l’amélioration de la vitesse en vaut la peine.

Une autre nouvelle fonctionnalité du compilateur pour la version 12.3 est que FunctionCompile peut maintenant prendre une liste ou une association de fonctions qui sont compilées ensemble, en optimisant avec toutes leurs interdépendances.

Le compilateur continue de se renforcer et de s’élargir, avec de plus en plus de fonctions et de types (comme « Integer128 ») pris en charge. Et pour soutenir les projets de compilation à grande échelle, un élément a été ajouté dans la version 12.3 : le CompilerEnvironmentObject. Il s’agit d’un objet symbolique qui représente toute une collection de ressources compilées (par exemple définies par FunctionDeclaration) qui agissent comme une bibliothèque et peuvent être immédiatement utilisées pour fournir un environnement pour une compilation supplémentaire en cours.

Shell, Java, … : Nouvelles connexions externes intégrées

Au cours des dernières versions, nous avons ajouté la prise en charge d’interactions directes avec une série de langages externes, à la fois de manière programmatique par le biais de fonctions telles que ExternalEvaluate, et en tant que parties de notebooks. La version 12.3 ajoute la prise en charge de plusieurs langues supplémentaires.

Tout d’abord, il y a l’interpréteur de commandes. Dans la version 1.0, il y avait la notion d' »échappement de l’interpréteur de commandes » : tapez ! au début d’une ligne, et tout ce qui suit est envoyé à l’interpréteur de commandes de votre système d’exploitation. Un tiers de siècle plus tard, cette notion est un peu plus élaborée et sophistiquée, bien qu’il s’agisse de la même idée de base.

Tapez > dans un carnet de notes, et sélectionnez Shell, puis tapez votre commande shell :

Le stdout de l’interpréteur de commandes sera répercuté tel qu’il est généré, et ce qui reviendra sera un objet symbolique – à partir duquel il est possible d’extraire des choses comme le code de sortie, ou le stdout :

Dans les versions précédentes, nous avons ajouté des capacités pour des langages comme Python, Julia, R, etc., ainsi que SQL. Dans cette version, nous ajoutons également le support d’Octave (oui, les noms des fonctions ne sont pas géniaux) :

Mais le point important ici est que les structures de données ont été connectées de façon à ce qu’un tableau Octave revienne sous la forme d’une expression appropriée, dans ce cas une liste de listes (contenant des nombres approximatifs, car c’est tout ce qu’Octave gère).

À propos, bien que les cellules de langage externe dans les carnets soient agréables, vous n’êtes absolument pas obligé de les utiliser, et vous pouvez utiliser ExternalEvaluate – ou ExternalFunction – pour faire les choses de manière purement programmatique.

Depuis plus de 20 ans, nous avons une intégration étroite avec Java dans Wolfram Language par le biais de J/Link. Mais dans la version 12.3, nous avons fait en sorte qu’au lieu d’utiliser l’interface symbolique sophistiquée de J/Link avec Java, vous pouvez simplement saisir le code Java directement dans ExternalEvaluate et les cellules de langage externe :

Les structures de données Java de base sont renvoyées comme des expressions standard du Wolfram Language :

Java objects are represented symbolically through J/Link:

Tout interagit de manière transparente avec J/Link. Et par exemple, vous pouvez créer des objets Java directement à l’aide de J/Link – que vous pouvez ensuite utiliser avec le Java que vous saisissez dans une cellule de langage externe :

Si vous définissez une fonction Java, elle est représentée symboliquement comme un objet ExternalFunction :

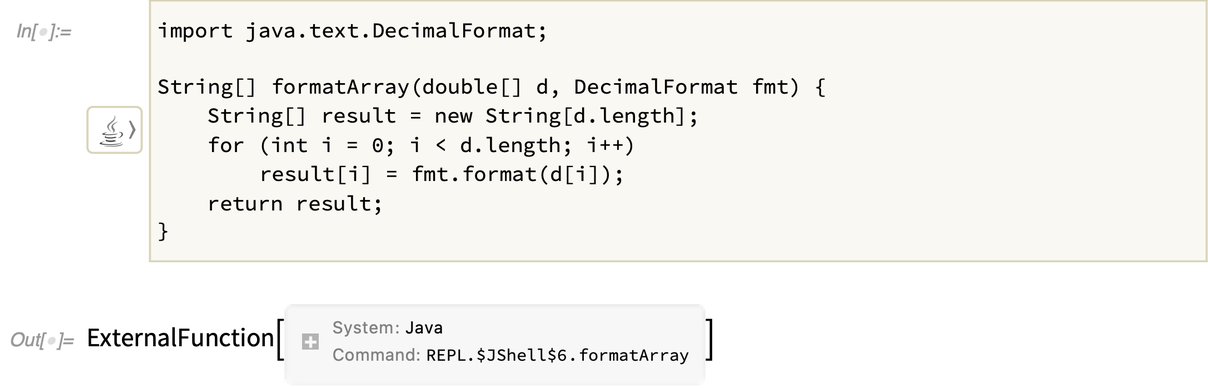
Cette fonction particulière prend une liste de nombres et un objet Java du type de celui que nous avons créé ci-dessus avec J/Link :

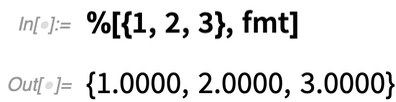
(Oui, cette opération particulière est extrêmement facile à réaliser directement dans le Wolfram Language).

Blockchain, stockage, authentification et cryptographie

Nous avons d’abord introduit la fonctionnalité blockchain dans Wolfram Language dans la version 11.3 (2018), et dans chaque version successive, nous ajoutons de plus en plus d’intégration blockchain. La version 12.3 ajoute la connectivité à la blockchain Tezos :

En plus de faire des transactions blockchain et des analyses blockchain avec Wolfram Language, nous faisons aussi de plus en plus de contrats computationnels – pour lesquels le caractère de langage computationnel à part entière du Wolfram Language donne des opportunités uniques (un exemple étant la création d' » oracles » basés sur nos connaissances computationnelles sur le monde).

Dans la version 12.1, nous avons introduit ExternalStorageObject, prenant initialement en charge IPFS et Dropbox. Dans la version 12.3, nous avons ajouté la prise en charge d’Amazon S3 (et, oui, vous pouvez stocker et récupérer un seau entier de fichiers à la fois) :

L’authentification est une étape nécessaire dans toutes sortes d’interactions externes. Dans la version 12.3, nous avons ajouté la prise en charge des flux de travail OAuth 2.0. Vous créez une SecuredAuthenticationKey :

Vous pouvez alors faire une demande en utilisant cette clé :

Une fenêtre du navigateur vous demandera de vous connecter avec votre compte, puis vous serez opérationnel.

Pour de nombreux services externes courants, nous avons des connexions ServiceConnect « prêtes à l’emploi ». Elles nécessitent souvent une authentification. Et pour les API basées sur OAuth (comme Reddit ou Twitter), nous avons notre application WolframConnector qui sert d’intermédiaire pour la partie externe de l’authentification. Une nouvelle fonctionnalité de la version 12.3 est que vous pouvez également utiliser votre propre application externe pour négocier cette authentification, de sorte que vous n’êtes pas limité par les dispositions prises avec le service externe pour l’application WolframConnector.

La cryptographie est à la base de tout ce dont nous parlons ici. Dans la version 12.3, nous avons ajouté de nouvelles capacités cryptographiques ; en particulier, nous prenons désormais en charge toutes les courbes elliptiques de la norme FIPS 186-4 de signature numérique du NIST, ainsi que les courbes Edwards qui feront partie de la norme FIPS 186-5.

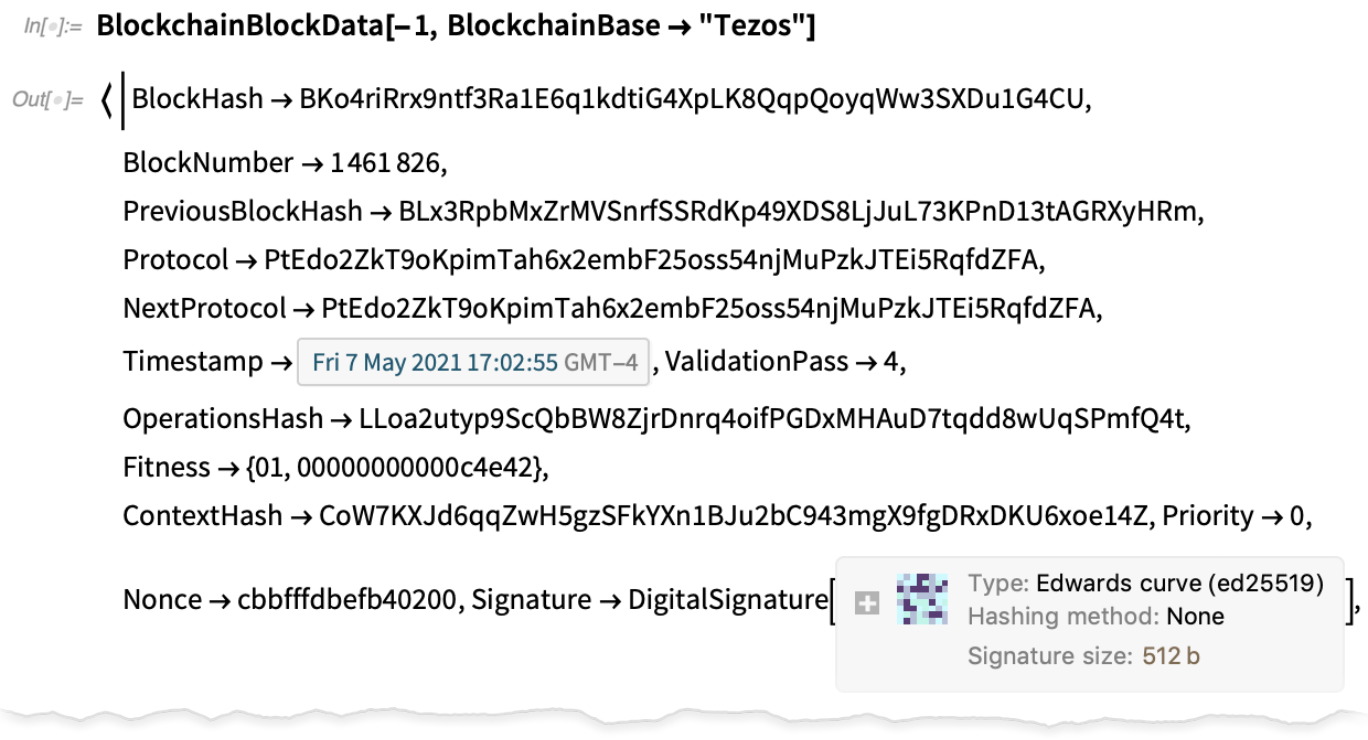
Nous avons regroupé tout cela pour faciliter la création de portefeuilles de blockchain, la signature de transactions et l’encodage de données pour les blockchains :

Informatique distribuée et sa gestion

Le calcul parallèle a été introduit pour la première fois dans le langage Wolfram au milieu des années 1990. Dans la version 7.0 (2008), nous avons introduit des fonctions telles que ParallelMap et Parallelize. Il a toujours été simple de mettre en place un calcul parallèle sur plusieurs cœurs d’un même ordinateur. Mais cela s’est avéré plus compliqué lorsque l’on souhaite également utiliser des ordinateurs distants.

Dans la version 12.2, nous avons introduit RemoteKernelObject comme représentation symbolique des capacités distantes du Wolfram Language. À partir de la version 12.2, cette représentation était disponible pour les évaluations ponctuelles avec RemoteEvaluate. Dans la version 12.3, nous avons intégré RemoteKernelObject dans le calcul parallèle.

Essayons ceci pour une de mes machines. Voici un objet noyau distant qui représente un seul noyau sur celui-ci :

Nous pouvons maintenant effectuer un calcul à cet endroit, en demandant simplement le nombre de cœurs du processeur :

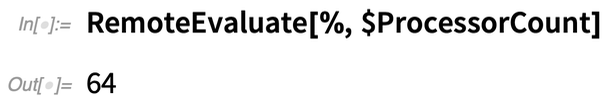
Créons maintenant un objet noyau distant qui utilise les 64 cœurs de cette machine :

Maintenant je peux lancer ces noyaux (et, oui, c’est beaucoup plus rapide et plus robuste qu’avant) :

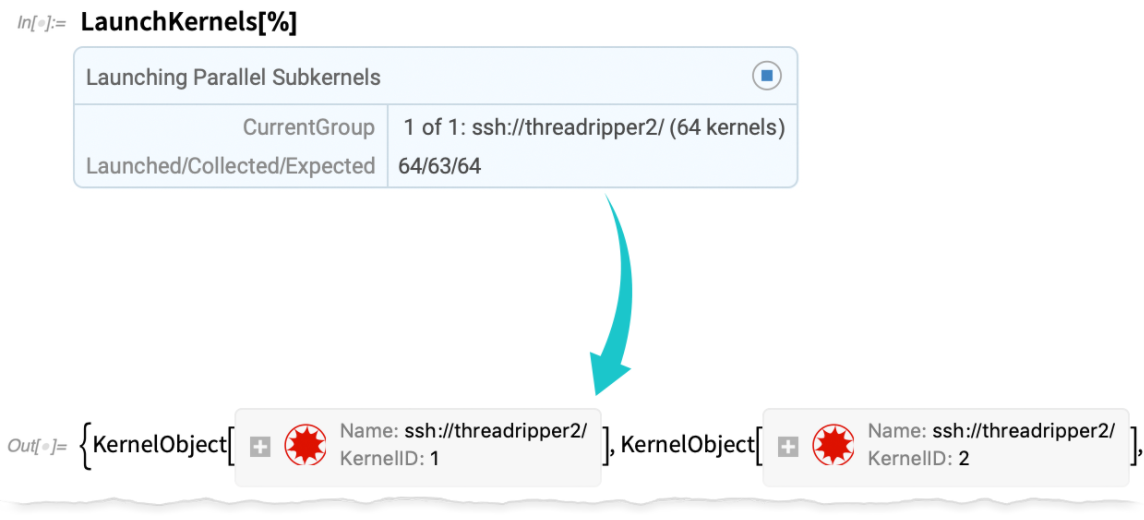
Je peux maintenant l’utiliser pour faire des calculs parallèles :

Pour quelqu’un comme moi qui est souvent impliqué dans des calculs parallèles, la rationalisation de ces capacités dans la version 12.3 fera une grande différence.

Une des caractéristiques des fonctions comme ParallelMap est qu’elles se contentent d’envoyer des parties d’un calcul indépendamment à différents processeurs. Les choses peuvent devenir assez compliquées lorsqu’il faut communiquer entre les processeurs et que tout se passe de manière asynchrone.

La science de base de ce phénomène est profondément liée à l’histoire des graphes multivoie et aux origines de la mécanique quantique dans notre projet de physique. Mais au niveau pratique de l’ingénierie logicielle, il s’agit de conditions de course, de sécurité des threads, de verrouillage, etc. Dans la version 12.3, nous avons ajouté quelques fonctionnalités à ce sujet.

En particulier, nous avons ajouté la fonction WithLock qui peut verrouiller des fichiers (ou des objets locaux) pendant un calcul, empêchant ainsi les interférences entre les différents processus qui tentent d’écrire dans le fichier. WithLock fournit un mécanisme de bas niveau pour assurer l’atomicité et la sécurité thread des opérations.

Il existe une version de plus haut niveau de ceci dans LocalSymbol. Disons que l’on met un symbole local à 0 :

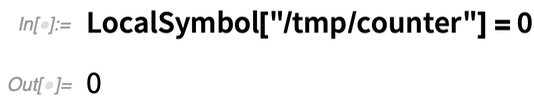
Ensuite, lancez 40 noyaux parallèles locaux (ils doivent être locaux pour pouvoir partager des fichiers) :

Maintenant, à cause du verrouillage, le compteur sera obligé de se mettre à jour séquentiellement sur chaque noyau :

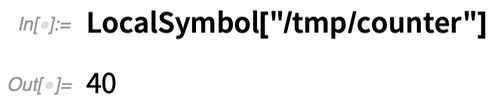
Pour en savoir plus, voir :

12.3 Livecoding & Q&A avec Stephen Wolfram » (VIDÉO)

Téléchargez votre 12.3 maintenant ! » (Il est déjà en ligne dans le Wolfram Cloud !)