New In 
Media modelului bayesian (BMA) pentru regresia liniară
De ce să alegeți doar un singur model când puteți împrumuta informații de la mai multe? Noua suită bma realizează o medie Bayesiană a modelelor pentru a ține cont de incertitudinea modelului în analiza dumneavoastră. Nu sunteți sigur ce predictori să includeți în modelul dvs. de regresie liniară? Utilizați bmaregress pentru a afla care sunt predictorii importanți. Efectuați alegerea modelului, inferența și predicția. Utilizați numeroase comenzi de post-estimare pentru a explora modelele influente, complexitatea modelului, potrivirea modelului și performanța predictivă, analiza sensibilității la ipotezele privind importanța modelelor și a predictorilor și multe altele.
Repere
-
Alegerea modelului, inferența și predicția
-
Enumerarea modelelor și eșantionarea MC3
-
Predictori întotdeauna incluși și grupați
-
Priori de model: uniform, binomial, beta-binomial
-
Multe priorități g, inclusiv hiper-g și robustă
-
Variabile factoriale și operatori de serii temporale
-
Ereditate puternică, slabă sau fără ereditate pentru interacțiuni
-
Convergența BMA MCMC
-
Modelul posterior și probabilitățile de includere
-
Distribuțiile anterioare și posterioare ale mărimii modelului
-
Distribuțiile posterioare ale parametrilor modelului
-
Măsuri de conexitate pentru perechi de predictori
-
Hărți cu incluziune de variabile
-
Log predictive-score pentru potrivirea modelului și performanța predicției
-
Analiza de sensibilitate
-
Predicție
-
Suportul standard al funcțiilor de post-estimare Bayesiană
-
Vezi mai mult Media modelului bayesian caracteristici
Introducere
În mod tradițional, selectăm un model și efectuăm inferențe și predicții condiționate de acest model. De obicei, rezultatele noastre nu țin cont de incertitudinea în selectarea unui model și, prin urmare, pot fi prea optimiste. Ele pot fi chiar incorecte dacă modelul selectat este substanțial diferit de adevăratul model generator de date (DGM). În unele aplicații, este posibil să dispunem de dovezi teoretice sau empirice solide cu privire la DGM. În alte aplicații, de obicei de natură complexă și instabilă, cum ar fi cele din economie, psihologie și epidemiologie, alegerea unui model fiabil poate fi dificilă. În loc să se bazeze pe un singur model, medierea modelelor face o medie a rezultatelor pe mai multe modele plauzibile bazate pe datele observate. În BMA, „plauzibilitatea” modelului este descrisă de probabilitatea modelului posterior (PMP), care este determinată cu ajutorul principiilor bayesiene fundamentale – teorema lui Bayes – și aplicată în mod universal la toate analizele de date. BMA poate fi utilizată pentru a ține cont de incertitudinea modelului atunci când se estimează parametrii modelului și se prezic noi observații pentru a evita concluziile prea optimiste. Este deosebit de utilă în aplicații cu mai multe modele plauzibile, în cazul în care nu există un motiv definitiv pentru a alege un anumit model în detrimentul celorlalți. Dar chiar dacă alegerea unui singur model este obiectivul final, BMA poate fi benefică. Aceasta oferă o modalitate bazată pe principii pentru a identifica modelele și predictorii importanți în cadrul claselor de modele luate în considerare. Cadrul său vă permite să aflați despre interrelațiile dintre diferiți predictori în ceea ce privește tendința lor de a apărea într-un model împreună, separat sau independent. Acesta poate fi utilizat pentru a evalua sensibilitatea rezultatelor finale la diverse ipoteze privind importanța diferitelor modele și predictori. Și oferă predicții optime în sensul log-score.
Suita bma
Într-un context de regresie, incertitudinea modelului reprezintă incertitudinea cu privire la predictorii care ar trebui incluși într-un model. Putem utiliza bmaregress pentru a ține cont de selecția predictorilor într-o regresie liniară. Acesta explorează spațiul modelului fie în mod exhaustiv cu opțiunea de enumerare, ori de câte ori este posibil, fie prin utilizarea algoritmului de compoziție a modelelor (MC3) Markov chain Monte Carlo (MCMC) cu opțiunea de eșantionare. Raportează diverse rezumate ale modelelor vizitate și ale predictorilor incluși, precum și ale distribuțiilor posterioare ale parametrilor modelului. Vă permite să specificați grupuri de predictori care să fie incluși sau excluși împreună dintr-un model și cei care sunt incluși în toate modelele. Oferă diverse distribuții anterioare pentru modele în opțiunea mprior() și pentru parametrul g, care controlează micșorarea coeficienților de regresie spre zero, în opțiunea gprior(). De asemenea, suportă variabilele factoriale și operatorii de serii temporale și oferă mai multe modalități de tratare a interacțiunilor în timpul estimării prin utilizarea opțiunii heredity().
Există multe funcții de postestimare acceptate, care includ, de asemenea, unele dintre funcțiile standard de postestimare bayesiană.
| Comandă | Descriere |
|---|---|
|
Eșantioane posterioare ale coeficienților de regresie |
|
|
diagrame model-probabilitate |
|
|
diagrame de distribuție a dimensiunilor modelului |
|
|
hărți cu includere de variabile |
|
|
diagrame de densitate posterioară a coeficientului |
|
|
rezumatele modelului posterior și ale includerii variabilelor |
|
|
rezumat al dimensiunii modelului |
|
|
probabilități ulterioare de includere (PIP) pentru predictori |
|
|
măsuri de îmbinare pentru predictori |
|
|
scorul predictiv logaritmic (LPS) |
|
|
Predicțiile BMA |
|
|
Rezumate grafice bayesiene și diagnostice de convergență |
|
|
Statistici sumare bayesiene pentru parametrii modelului și funcțiile acestora |
|
|
Mărimile efective ale eșantioanelor Bayesiene și statisticile aferente |
|
|
Valorile p predictive bayesiene |
|
|
Predicții bayesiene |
Să vedem cum funcționează
-> Enumerarea modelului -> Intervale credibile -> Modele influente -> Predictori importanți ->Distribuția dimensiunilor modelului -> Distribuțiile posterioare ale coeficienților -> Predicția BMA -> Priori de model informativ -> Performanță predictivă utilizând LPS -> Curățare
Mai jos, oferim un tur al unor caracteristici bma folosind un set de date de jucărie. Acest set de date conține n=200
�=200 observații, p=10 �=10 predictori ortogonali, iar rezultatul y generat sub forma
y=0,5+1,2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
unde ϵ∼∼N(0,1)
�∼�(0,1) este un termen de eroare normal standard.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Enumerarea modelului
Utilizăm bmaregress pentru a ajusta o regresie liniară BMA a lui y la x1 până la x10.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
Cu 10 predictori și g-prior fix (de referință) implicit, bmaregress utilizează enumerarea modelelor și explorează toate cele 210=1.024
210=1.024 modele posibile. Prioritatea implicită a modelului este beta-binomial cu parametrii de formă de 1, care este uniformă pe dimensiunea modelului. A priori, modelul nostru BMA a presupus o micșorare mică a coeficienților de regresie spre zero, deoarece g/(1+g)=0,9950 �/(1+�)=0,9950 este aproape de 1.
bmaregress a identificat x2 și x10 ca fiind predictori foarte importanți – probabilitățile lor de includere posterioare (PIP) sunt în esență 1. Estimările medii posterioare ale coeficienților lor de regresie sunt, respectiv, 1,2 (rotunjite) și 5,1 și sunt foarte apropiate de valorile reale de 1,2 și 5. Toți ceilalți predictori au PIP-uri mult mai mici și estimări ale coeficienților apropiate de zero. Constatările noastre BMA sunt în concordanță cu adevăratul DGM.
Să stocăm rezultatele actuale ale estimării noastre pentru utilizare ulterioară. Ca și în cazul altor comenzi bayesiene, trebuie să salvăm mai întâi rezultatele simulării înainte de a putea utiliza estimates store pentru a stoca rezultatele estimării.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Intervale credibile
bmaregress nu raportează în mod implicit intervale credibile (CrIs), deoarece necesită o simulare potențial consumatoare de timp a eșantionului posterior de parametri ai modelului. Dar le putem calcula după estimare.
Utilizăm mai întâi bmacoefsample pentru a genera un eșantion MCMC din distribuția posterioară a parametrilor modelului, care include coeficienții de regresie. Apoi folosim comanda bayesstats summary existentă pentru a calcula rezumatele posterioare ale eșantionului MCMC generat.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
CrI de 95% pentru coeficientul x2 este [1,05, 1,34], iar cel pentru x10 este [4,9, 5,26], ceea ce este în concordanță cu DGM-ul nostru.
Modele influente
Estimările coeficienților BMA sunt mediate pe 1 024 de modele. Este important să se investigheze ce modele sunt influente. Putem utiliza modelele bmastats pentru a explora PMP-urile.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Nu este surprinzător faptul că modelul care conține atât x2, cât și x10 are cel mai mare PMP, de aproximativ 63%. De fapt, primele două modele corespund unui PMP cumulat de aproximativ 77%:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
Putem utiliza bmagraph pmp pentru a reprezenta grafic PMP cumulat.
. bmagraph pmp, cumulative

Comanda afișează în mod implicit primele 100 de modele, dar puteți specifica opțiunea top() dacă doriți să vedeți mai multe modele.
Predictori importanți
Putem explora vizual importanța predictorilor folosind bmagraph varmap pentru a produce o hartă de includere a variabilelor.
. bmagraph varmap Computing model probabilities ...

x2 și x10 sunt incluse în toate cele 100 de modele de top, clasificate în funcție de PMP. Coeficienții acestora sunt pozitivi în toate modelele.
Distribuția dimensiunilor modelului
Putem explora complexitatea modelului nostru BMA folosind bmastats msize și bmagraph msize pentru a explora distribuțiile anterioare și posterioare ale dimensiunii modelului.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
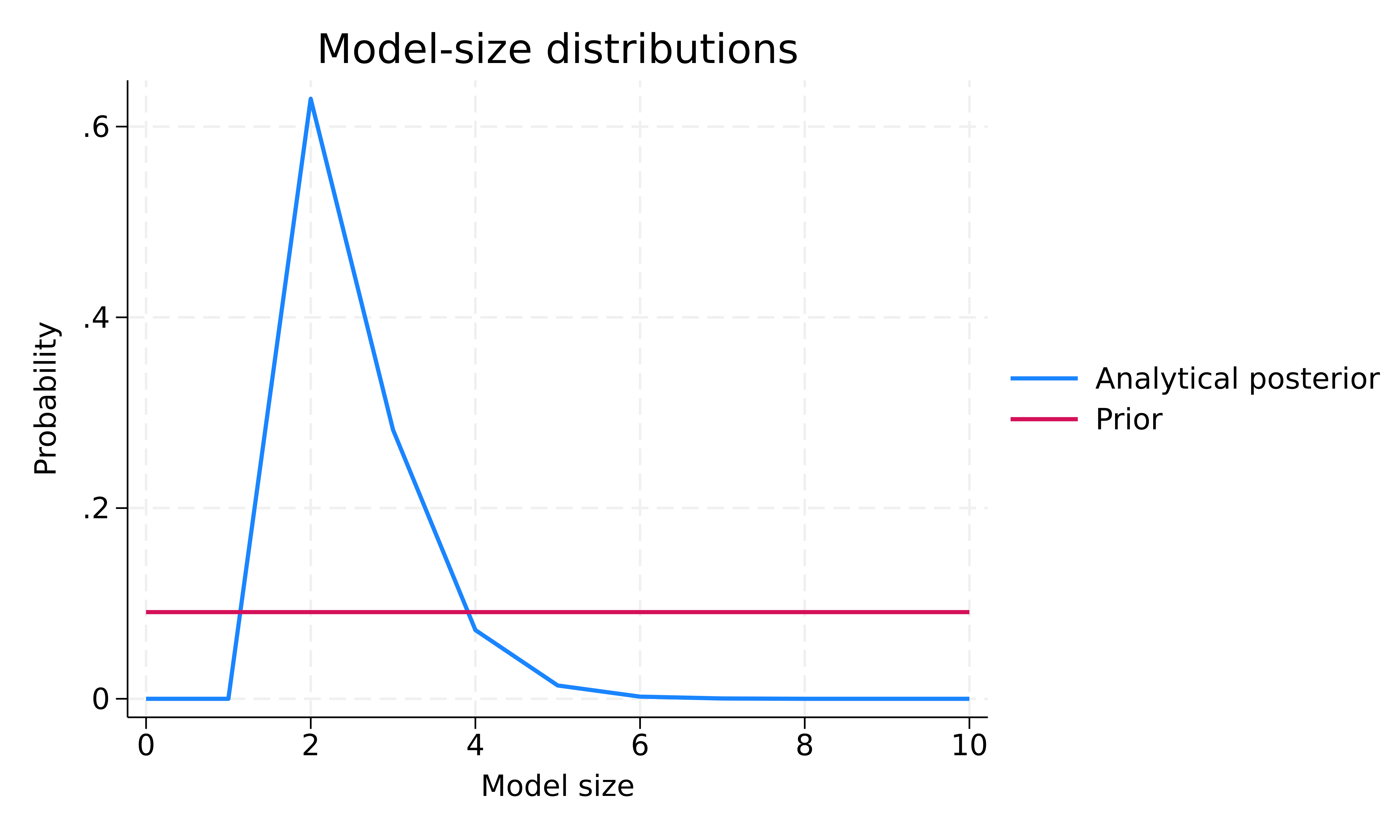
Distribuția anterioară a mărimii modelului este uniformă în funcție de mărimea modelului. Distribuția posterioară a dimensiunii modelului este înclinată spre stânga, cu un mod de aproximativ 2. Media anterioară a dimensiunii modelului este 5, iar cea posterioară este 2,48. Astfel, pe baza datelor observate, BMA tinde să favorizeze modele mai mici, cu aproximativ doi predictori, în medie, în comparație cu ipoteza noastră a priori.
Distribuțiile posterioare ale coeficienților
Putem utiliza bmagraph coefdensity pentru a trasa distribuțiile posterioare ale coeficienților de regresie.
. bmagraph coefdensity {x2} {x3}, combine
Aceste distribuții sunt amestecuri de o masă punctiformă la zero, care corespunde probabilității de neincludere a predictorului și o densitate continuă condiționată de includere. Pentru coeficientul x2, probabilitatea de neincludere este neglijabilă, astfel încât distribuția sa posterioară este, în esență, o densitate continuă, destul de simetrică, centrată la 1,2. Pentru coeficientul x3, în plus față de densitatea continuă condiționată, există o linie verticală roșie la zero care corespunde probabilității posterioare de neincludere de aproximativ 1-,2 = 0,8.
Predicția BMA
bmapredict produce diverse predicții BMA. De exemplu, să calculăm mediile predictive posterioare.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
De asemenea, putem calcula CRI predictive pentru a estima incertitudinea cu privire la predicțiile noastre. (Acest lucru nu este disponibil în cazul multor metode tradiționale de selecție a modelelor.) Rețineți că aceste ICR predictive încorporează, de asemenea, incertitudinea modelului. Pentru a calcula ICR predictive, trebuie să salvăm mai întâi eșantionul MCMC posterior de parametri de model-parametru.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Rezumăm rezultatele previzionate:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Mediile raportate pe observații pentru mediile predictive și limitele inferioare și superioare de 95% ale CrI predictive par rezonabile în raport cu rezultatul observat y.
Priori de model informativ
Unul dintre punctele forte ale BMA este capacitatea de a încorpora informații prealabile despre modele și predictori. Acest lucru ne permite să investigăm sensibilitatea rezultatelor la diferite ipoteze privind importanța modelelor și a predictorilor. Să presupunem că dispunem de informații fiabile conform cărora toți predictorii, cu excepția lui x2 și x10, sunt mai puțin probabil să fie legați de rezultat. Putem specifica, de exemplu, un model binomial anterior cu probabilități de includere anterioare scăzute pentru acești predictori.
Pentru a compara ulterior performanța în afara eșantionului a modelelor BMA, împărțim aleatoriu eșantionul nostru în două părți și ajustăm modelul BMA utilizând primul subeșantion. De asemenea, salvăm rezultatele acestui model BMA mai informativ.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Efectul acestui model anterior este că PIP al tuturor predictorilor neimportanți este acum mai mic de 2%.
Rețineți că, atunci când selectăm un model, în esență, potrivim un model BMA cu un prior foarte puternic conform căruia toți predictorii selectați trebuie să fie incluși cu o probabilitate de 1. De exemplu, putem forța bmaregress să includă toate variabilele în model:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Performanță predictivă utilizând LPS
Pentru a compara modelele BMA avute în vedere, refacem modelul nostru BMA implicit folosind primul subeșantion și stocăm rezultatele estimării.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Putem compara performanța predictivă în afara eșantionului a modelelor noastre BMA folosind bmastats lps pentru a calcula scorul predictiv logaritmic (LPS) pentru observațiile în afara eșantionului.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Modelul bmareg_inf, mai informativ, are un LPS mediu ușor mai mic, dar rezumatele LPS pentru toate modelele sunt foarte asemănătoare. Consultați [BMA] bmastats lps pentru a vedea cum se compară performanța modelelor BMA prin utilizarea validării încrucișate.
Curățare
Am generat mai multe seturi de date în timpul analizei noastre. Nu mai avem nevoie de ele, așa că le ștergem la sfârșit. Dar este posibil să decideți să le păstrați, mai ales dacă ele corespund unei analize finale care ar putea consuma mult timp.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
