Nou în 
Prognoză dinamică bayesiană
Prognozarea dinamică este un instrument de predicție obișnuit după montarea modelelor multivariate de serii temporale, cum ar fi modelele vector autoregresive (VAR). Acesta prezice valorile rezultatelor la un moment curent utilizând valorile actualizate (prezise) ale rezultatelor în timpurile anterioare. Noua comandă bayesfcast calculează previziunile dinamice bayesiene după montarea unui model VAR Bayesian utilizând comanda bayes: var.
Prognozele dinamice bayesiene produc un eșantion întreg de valori de rezultat prezise la fiecare punct de timp în loc de o singură predicție ca în analiza clasică. Acest eșantion poate fi utilizat pentru a răspunde la diferite întrebări de modelare, cum ar fi cât de bine modelul prezice observații viitoare fără a face presupunerea asimptotică a normalității atunci când se estimează incertitudinea prognozată. Acest lucru este deosebit de atrăgător pentru seturile de date mici pentru care presupunerea asimptotică a normalității poate fi suspectă.
Puteți utiliza calculul bayesfcast pentru a calcula prognozele dinamice și a le salva în setul de date curent și le puteți grafica folosind bayesfcast graph.
Să vedem cum funcționează
Continuăm cu datele macro din SUA din modelele Bayesiene VAR, care sunt date trimestriale din primul trimestru al anului 1954 până în al patrulea trimestru al anului 2010. Am dori să obținem previziuni dinamice bayesiene ale inflației, decalajului de producție și rata fondurilor federale dintr-un VAR Bayesian model pentru aceste variabile.
Iată cum arată datele.
. webuse usmacro
(Federal Reserve Economic Data - St. Louis Fed)
. tsset
Time variable: date, 1954q3 to 2010q4
Delta: 1 quarter
. tsline inflation ogap fedfunds

Ieșirea din comanda bayes: var este lungă, așa că omitem o parte din aceasta mai jos.
. bayes, rseed(17) saving(bvarsim): var inflation ogap fedfunds if date < tq(2004q1), lags(1/4)
Burn-in ...
Simulation ...
(output omitted)
Bayesian vector autoregression MCMC iterations = 12,500
Gibbs sampling Burn-in = 2,500
MCMC sample size = 10,000
Sample: 1956q3 thru 2003q4 Number of obs = 190
Acceptance rate = 1
Efficiency: min = .9322
avg = .993
Log marginal-likelihood = -670.32584 max = 1
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| inflation | ||
| inflation | ||
| L1. | 1.107465 .0422849 .000423 1.106848 1.02544 1.192476 | |
| L2. | -.064825 .0417594 .000418 -.064536 -.1470882 .0176208 | |
| L3. | -.0358872 .0290815 .000291 -.0359867 -.092745 .0210088 | |
| L4. | -.0397985 .0215853 .000216 -.0397207 -.0821996 .002274 | |
| ogap | ||
| L1. | .0646785 .0294384 .000305 .0644936 .0070243 .1229662 | |
| L2. | .0071294 .0267595 .000268 .0072498 -.0444994 .058461 | |
| L3. | -.002015 .0187035 .000192 -.0021291 -.038934 .0346847 | |
| L4. | -.0088532 .0142951 .000141 -.0089083 -.0366927 .0193774 | |
| fedfunds | ||
| L1. | .0770026 .027543 .000275 .076643 .0237776 .1315991 | |
| L2. | -.0351476 .0243814 .000244 -.0351349 -.0831241 .0124089 | |
| L3. | -.0151671 .0173423 .000173 -.0154901 -.0487873 .0193082 | |
| L4. | -.0190271 .0134133 .000134 -.0191324 -.0456025 .0072003 | |
| _cons | .1225433 .0832813 .000833 .1225758 -.0433392 .2853939 | |
| ogap | ||
| inflation | ||
| L1. | -.068909 .0627925 .000628 -.0683572 -.1934463 .0524915 | |
| (output omitted) | ||
| _cons | .3851112 .1261445 .001261 .3836084 .1334414 .6333448 | |
| fedfunds | ||
| inflation | ||
| L1. | .0568126 .0719825 .00072 .0563617 -.0829406 .2008528 | |
| (output omitted) | ||
| _cons | .1931161 .1433129 .001433 .1950842 -.0912408 .4717853 | |
| Sigma_1_1 | .2873009 .0293728 .000297 .2853721 .2349716 .3493519 | |
| Sigma_2_1 | .0281781 .0315254 .000315 .0276486 -.0345647 .0912571 | |
| Sigma_3_1 | .1480748 .0372496 .000372 .1468518 .0777631 .2251876 | |
| Sigma_2_2 | .6575456 .0671182 .000684 .6530136 .5395734 .8029292 | |
| Sigma_3_2 | .2398338 .0559347 .000559 .238127 .1357633 .3561841 | |
| Sigma_3_3 | .8371554 .0857785 .000858 .8298623 .6868505 1.024522 | |
Consultați modelul Bayesian VAR pentru detalii despre bayes: var și rezultatul acestuia.
Folosim noua comandă bayesfcast pentru a calcula prognozele dinamice bayesiene. Această comandă are două subcomenzi. bayesfcast compute calculează previziunile și le salvează în setul de date curent ca variabile noi. Și graficul bayesfcast prezintă prognozele.
Să începem cu cea mai simplă specificație. Specificăm f_ ca prefix pentru noile variabile și un seed aleatoriu pentru reproductibilitate.
. bayesfcast compute f_, rseed(17) . describe f_*
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| f_inflation double %10.0g Posterior mean forecast for | ||
| inflation | ||
| f_inflation_sd double %10.0g Posterior standard deviation of | ||
| forecast for inflation | ||
| f_inflation_lb double %10.0g 95% lower credible bound for | ||
| forecast for inflation | ||
| f_inflation_ub double %10.0g 95% upper credible bound for | ||
| forecast for inflation | ||
| f_ogap double %10.0g Posterior mean forecast for ogap | ||
| f_ogap_sd double %10.0g Posterior standard deviation of | ||
| forecast for ogap | ||
| f_ogap_lb double %10.0g 95% lower credible bound for | ||
| forecast for ogap | ||
| f_ogap_ub double %10.0g 95% upper credible bound for | ||
| forecast for ogap | ||
| f_fedfunds double %10.0g Posterior mean forecast for | ||
| fedfunds | ||
| f_fedfunds_sd double %10.0g Posterior standard deviation of | ||
| forecast for fedfunds | ||
| f_fedfunds_lb double %10.0g 95% lower credible bound for | ||
| forecast for fedfunds | ||
| f_fedfunds_ub double %10.0g 95% upper credible bound for | ||
| forecast for fedfunds | ||
bayesirf compute creează noi variabile care conțin diverse statistici sumare pentru prognoze. Spre deosebire de analiza clasică, o prognoză bayesiană la un moment specific nu corespunde doar unei valori, ci unui eșantion de valori MCMC. Aceste valori sunt apoi sintetizate (ca mijloace sau mediane) pentru a furniza o singură statistică. În mod implicit, comanda calculează mijloacele posterioare, abaterile standard posterioare și 95% intervale credibile cu coadă egală pentru prognoza pentru fiecare variabilă de rezultat.
Să trasăm prognozele implicite și benzile lor credibile de 95%.
. bayesfcast graph f_inflation f_ogap f_fedfunds

În mod implicit, obținem prognoze pentru o perioadă. Mai târziu vom arăta cum să creăm prognoze cu mai multe perioade.
În loc de prognoze medii posterioare și intervale credibile cu coadă egală, putem calcula prognoze mediane posterioare și intervale credibile de densitate posterioară mai mare (HPD). Le calculăm și le trasăm mai jos.
. bayesfcast compute f_, rseed(17) median hpd replace . bayesfcast graph f_inflation f_ogap f_fedfunds
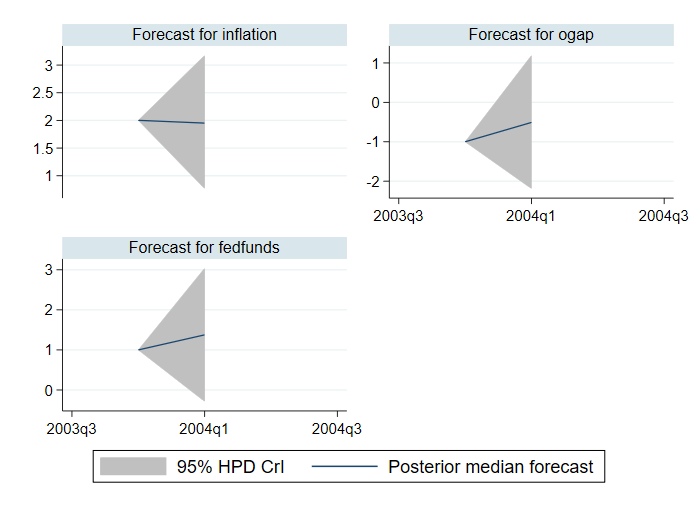
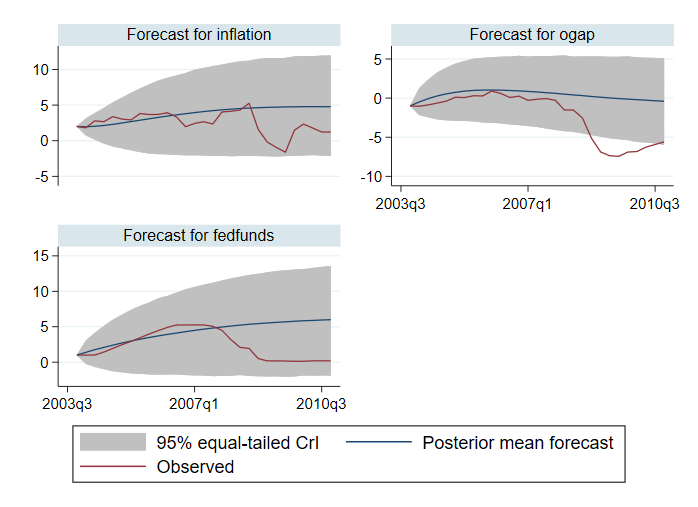
. bayesfcast compute f_, step(28) rseed(17) replace . bayesfcast graph f_inflation f_ogap f_fedfunds, observed
Comparăm prognozele noastre cu valorile observate. Previziunile par să funcționeze bine în prezicerea rezultatelor până în 2007. După aceea, au performanțe slabe. De exemplu, intervalele credibile de 95% pentru intervalul de ieșire nu conțin valorile observate pentru o parte din orizontul de timp.
După analiză, eliminăm fișierul de simulare MCMC salvat de bayes: var.
. erase bvarsim.dta
