Přehled

Nový příkaz reri odhaduje aditivní interakce v binomických zobecněných lineárních modelech, logistických, Poissonových a negativních binomických regresích a v Coxových a dalších modelech přežití.

Oboustranné interakce v modelech, které odhadují RR, jsou obvykle vyjádřeny jako multiplikativní interakce. U mnoha biologických procesů však může aditivní model interakce modelovat proces lépe než multiplikativní (viz např. Andersson et al. [2005]).

U binárních expozic A a B chceme často modelovat riziko pozitivního výsledku pro subjekty, které mají A i B, ve srovnání se subjekty, které mají pouze A, a subjekty, které mají pouze B. To znamená, že chceme zkoumat interakci A a B.

V multiplikativním modelu se předpokládá, že riziko pro subjekty s A a B se rovná riziku pouze pro A krát riziko pouze pro B. Pokud se riziko pro A a B rovná multiplikativnímu riziku, říkáme, že neexistuje interakce A a B. Pokud je riziko větší než multiplikativní riziko, říkáme, že existuje pozitivní interakce. Multiplikativní modely jsou výhodné, protože se snadno specifikují a je snadné testovat, zda je interakce větší (nebo menší) než multiplikativní.

V aditivním modelu se předpokládá, že riziko pro subjekty s A a B se rovná riziku pouze pro A plus riziku pouze pro B. U této hypotézy chceme zjistit, o kolik je riziko pro A a B větší (nebo menší) než aditivní riziko.

Statistika RERI je tento rozdíl rizik formulovaný pomocí RR (Rothman, Greenland a Lash 2008). Statistika RERI rovná 0 znamená, že riziko je aditivní. Kladná statistika RERI znamená, že riziko je superaditivní, a záporná statistika RERI znamená, že riziko je subaditivní. Test statistické významnosti statistiky RERI je přímočarý, ale není tak jednoduchý jako test pro multiplikativní model.

Kromě statistiky RERI příkaz reri uvádí dvě další související statistiky: AP a SI. AP je podíl rizika A a B v důsledku superaditivity expozic A a B. SI přetváří statistiku RERI spíše jako poměr než jako rozdíl.

Podívejme se, jak to funguje

Ilustrujeme reri na příkladu, který odhaduje riziko vrozených vad v důsledku expozice dusičnanům. Používáme simulovaný soubor dat (nitrates.dta), který napodobuje výsledky z práce Brender et al. (2013).

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Naším výsledným ukazatelem je tubus, který představuje defekty neurální trubice. Expozice jsou dvě míry příjmu dusičnanů: lék s hodnotami 0/1, což znamená expozici nitrosovatelným lékům, a dusičnany, rovněž s hodnotami 0/1, což představuje buď nízkou, nebo vysokou denní spotřebu dusičnanů z pitné vody.

Pro interakci léku a dusičnanů chceme použít aditivní model. Protože se jedná o observační studii, je vhodný binomický model rizika, který fitujeme pomocí binreg:

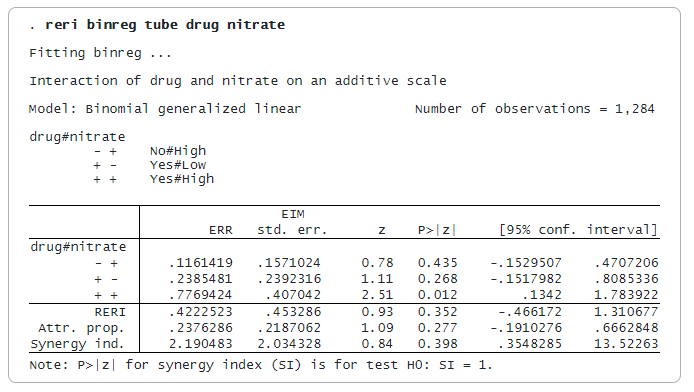
Interakce vytvořené pomocí reri představují nesouvislé skupiny v datech. Interakce -+ je pro lék = Ne a dusičnany = Vysoká. Interakce +- a ++ jsou definovány podobně, jak je uvedeno v legendě. Interakce — je referenční kategorie.

Odhady vedle -+, +- a ++ jsou míry nadměrného relativního rizika (ERR) definované jako RR minus jedna. ERR větší než 0 znamená, že RR je větší než 1.

Pokud je model aditivní, měli bychom následující hodnoty

  ERR(++) = ERR(-+) + ERR(+-)

Statistika RERI je rozdíl mezi oběma stranami této rovnice:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Odhad ERR(++) je 0,777, což je více než ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Model je tedy superaditivní. Statistika RERI je 0,422, což je rozdíl mezi 0,777 a 0,355.

Statistika AP je podíl rizika pro interakci ++, který je způsoben rizikem, které je nadaditivní. V našem příkladu je odhad AP 0,24. Statistika SI je nadměrné riziko vyjádřené spíše jako poměr než jako rozdíl. Její odhad 2,19 je větší než 1, což znamená pozitivní interakci nebo superaditivitu.

Kromě modelů binreg může reri fitovat logistický, poissonův, nbreg, stcox, stintcox, streg a stintreg model.

Odkazy

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic a A. Ahlbom. 2005. Výpočet měr biologické interakce. European Journal of Epidemiology 20: 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey a další. 2013. Prenatální příjem dusičnanů z pitné vody a vybrané vrozené vady u potomků účastníků National Birth Defects Prevention Study. Environmental Health Perspectives 121: 1083-1089.

Rothman, K. J., S. Greenland a T. L. Lash. 2008. Modern Epidemiology. Three ed. Philadelphia: Lippincott Williams & Wilkins.