Prezentare generală

Noua comandă reri estimează interacțiunile aditive în modelele liniare generalizate binomiale; regresiile logistice, Poisson și binomiale negative; și modelele Cox și alte modele de supraviețuire.

Interacțiunile bidirecționale în modelele care estimează RR sunt exprimate de obicei ca interacțiuni multiplicative. Cu toate acestea, pentru multe procese biologice, un model aditiv pentru interacțiune poate modela procesul mai bine decât unul multiplicativ (a se vedea, de exemplu, Andersson et al. [2005]).

Pentru expunerile binare A și B, deseori dorim să modelăm riscul unui rezultat pozitiv pentru subiecții care au avut atât A, cât și B, în comparație cu subiecții care au avut doar A și cei care au avut doar B. Altfel spus, dorim să examinăm interacțiunea dintre A și B.

Într-un model multiplicativ, se presupune că riscul pentru subiecții cu A și B este egal cu riscul pentru numai A înmulțit cu riscul pentru numai B. Dacă riscul pentru A și B este egal cu riscul multiplicativ, spunem că nu există interacțiune între A și B. Dacă riscul este mai mare decât riscul multiplicativ, spunem că există o interacțiune pozitivă. Modelele multiplicative sunt convenabile, deoarece sunt simplu de specificat și este ușor de testat dacă interacțiunea este mai mare (sau mai mică) decât cea multiplicativă.

Într-un model aditiv, se presupune că riscul pentru subiecții cu A și B este egal cu riscul doar pentru A plus riscul doar pentru B. Pentru această ipoteză, dorim să analizăm cu cât de mult riscul pentru A și B este mai mare (sau mai mic) decât riscul aditiv.

Statistica RERI reprezintă această diferență de risc formulată cu ajutorul RR (Rothman, Greenland și Lash 2008). O statistică RERI de 0 înseamnă că riscul este aditiv. O statistică RERI pozitivă înseamnă că riscul este supraaditiv, iar o statistică RERI negativă înseamnă că riscul este subaditiv. Testul de semnificație statistică a statisticii RERI este simplu, dar nu este la fel de simplu ca testul pentru modelul multiplicativ.

În afară de statistica RERI, comanda reri raportează alte două statistici conexe: AP și SI. AP este proporția de risc a lui A și B datorată superadditivității expunerilor A și B. SI reformulează statistica RERI ca un raport și nu ca o diferență.

Să vedem cum funcționează

Ilustrăm reri cu un exemplu care estimează riscul de malformații congenitale ca urmare a expunerii la nitrați. Utilizăm un set de date simulat (nitrates.dta) care imită rezultatele din Brender et al. (2013).

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Măsura noastră de rezultat este tubul, reprezentând defectele tubului neural. Expunerile sunt două măsuri ale consumului de nitrați: medicament, cu valori 0/1, care indică expunerea la medicamente nitrozabile; și nitrați, de asemenea cu valori 0/1, care reprezintă un consum zilnic scăzut sau ridicat de nitrați din apa de băut.

Dorim să ajustăm un model aditiv pentru interacțiunea dintre medicament și nitrați. Deoarece acesta este un studiu observațional, un model binomial de risc este adecvat și îl potrivim folosind binreg:

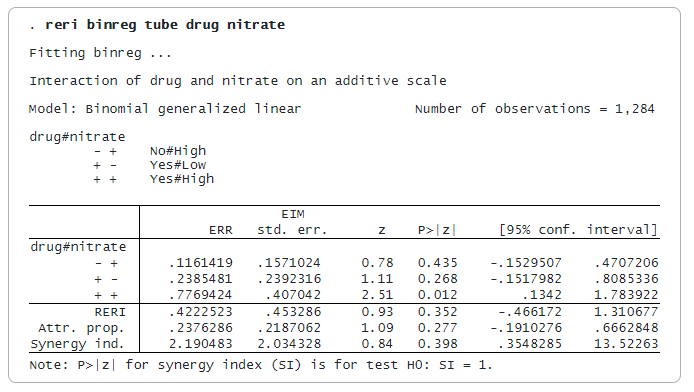
Interacțiunile create de reri reprezintă grupuri disjuncte în cadrul datelor. Interacțiunea -+ este pentru medicament = Nu și nitrat = Mare. Interacțiunile +- și ++ sunt definite în mod similar, așa cum se arată în legendă. Interacțiunea — reprezintă categoria de referință.

Estimările de lângă -+, +- și ++ sunt măsuri ale riscului relativ în exces (ERR), definit ca RR minus unu. ERR mai mare de 0 înseamnă că RR este mai mare de 1.

În cazul în care modelul este aditiv, am avea

  ERR(++) = ERR(-+) + ERR(+-)

Statistica RERI reprezintă diferența dintre cele două părți ale acestei ecuații:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Estimarea ERR(++) este de 0,777, care este mai mare decât ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Așadar, modelul este superadditiv. Statistica RERI este de 0,422, diferența dintre 0,777 și 0,355.

Statistica AP este proporția de risc pentru interacțiunea ++ care se datorează riscului care este supraaditiv. În exemplul nostru, estimarea AP este de 0,24. Statistica SI este excesul de risc exprimat ca un raport și nu ca o diferență. Estimarea sa de 2,19 este mai mare decât 1, ceea ce implică o interacțiune pozitivă sau superadditivitate.

Pe lângă modelele binreg, reri poate adapta modelele logistice, poisson, nbreg, stcox, stintcox, streg și stintreg.

Referințe

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic și A. Ahlbom. 2005. Calcularea măsurilor de interacțiune biologică. European Journal of Epidemiology 20: 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Aportul prenatal de nitrați din apa potabilă și defectele congenitale selectate la descendenții participanților la Studiul național de prevenire a defectelor congenitale. Environmental Health Perspectives 121: 1083-1089.

Rothman, K. J., S. Greenland și T. L. Lash. 2008. Modern Epidemiology. Ed. a 3-a. Philadelphia: Lippincott Williams & Wilkins.