Огляд

Нова команда reri оцінює адитивні взаємодії в біноміальних узагальнених лінійних моделях; логістичних, пуассонівських і від’ємних біноміальних регресіях; моделях Кокса та інших моделях виживання.

Двосторонні взаємодії в моделях, які оцінюють RR, зазвичай виражаються як мультиплікативні взаємодії. Однак для багатьох біологічних процесів адитивна модель взаємодії може моделювати процес краще, ніж мультиплікативна (див., наприклад, Andersson та ін. [2005]).

Для бінарних впливів А і В ми часто хочемо змоделювати ризик позитивного результату для суб’єктів, які мають і А, і В, порівняно з суб’єктами, які мають тільки А, і суб’єктами, які мають тільки В. Тобто, ми хочемо дослідити взаємодію А і В.

У мультиплікативній моделі передбачається, що ризик для суб’єктів з А і В дорівнює ризику тільки для А, помноженому на ризик тільки для В. Якщо ризик для А і В дорівнює мультиплікативному ризику, ми говоримо, що взаємодія між А і В відсутня. Якщо ризик більший, ніж мультиплікативний ризик, ми говоримо, що існує позитивна взаємодія. Мультиплікативні моделі зручні тим, що їх легко визначити, і легко перевірити, чи є взаємодія більшою (або меншою) за мультиплікативну.

В адитивній моделі передбачається, що ризик для суб’єктів з A і B дорівнює ризику тільки для A плюс ризик тільки для B. Для цієї гіпотези ми хочемо подивитися, наскільки ризик для A і B більший (або менший), ніж адитивний ризик.

Статистика RERI – це ця різниця ризиків, сформульована за допомогою RR (Rothman, Greenland, and Lash 2008). Статистика RERI, що дорівнює 0, означає, що ризик є адитивним. Позитивна статистика RERI означає, що ризик є суперадитивним, а негативна статистика RERI означає, що ризик є субадитивним. Перевірка статистичної значущості статистики RERI проста, але вона не така проста, як тест для мультиплікативної моделі.

Окрім статистики RERI, команда reri надає дві інші пов’язані статистики: AP та SI. AP – це частка ризику A і B, зумовлена суперадитивністю експозицій A і B. SI перетворює статистику RERI на відношення, а не на різницю.

Подивимося, як це працює

Ми проілюструємо reri на прикладі оцінки ризику вроджених вад розвитку від впливу нітратів. Ми використовуємо змодельований набір даних (nitrates.dta), який імітує результати дослідження Brender et al. (2013).

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Нашим показником результату є трубка, що представляє дефекти нервової трубки. Експозиції – це дві міри споживання нітратів: наркотики, зі значеннями 0/1, що вказують на нітрозуючий вплив наркотиків; і нітрати, також зі значеннями 0/1, що представляють або низьке, або високе щоденне споживання нітратів з питної води.

Ми хочемо підібрати адитивну модель для взаємодії наркотиків і нітратів. Оскільки це спостережне дослідження, доречною є біноміальна модель ризику, і ми підібрали її за допомогою binreg:

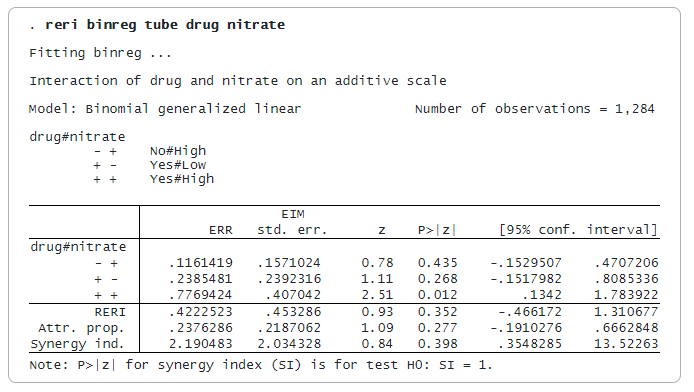
Взаємодії, створені reri, представляють розрізнені групи в даних. Взаємодія -+ для наркотиків = Ні та нітратів = Високий. Взаємодії +- і ++ визначаються аналогічно, як показано в легенді. Взаємодія — є базовою категорією.

Оцінки поруч з -+, +- і ++ є показниками надлишкового відносного ризику (ERR), який визначається як RR мінус одиниця. ERR більше 0 означає, що RR більше 1.

Якщо модель є адитивною, ми матимемо

  ERR(++) = ERR(-+) + ERR(+-)

Статистика RERI – це різниця між двома частинами цього рівняння:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Оцінка ERR(++) становить 0,777, що більше, ніж ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Отже, модель є суперадитивною. Статистика RERI становить 0,422, тобто різниця між 0,777 і 0,355.

Статистика AP – це частка ризику для взаємодії ++, яка зумовлена ризиком, що перевищує адитивний. У нашому прикладі оцінка AP дорівнює 0,24. Статистика SI – це надлишковий ризик, виражений як відношення, а не як різниця. Його оцінка 2,19 є більшою за 1, що означає позитивну взаємодію або суперадитивність.

Крім моделей binreg, reri може відповідати логістичним, пуассонівським, nbreg, stcox, stintcox, streg і stintreg моделям.

Посилання

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic, and A. Ahlbom. 2005. Calculating measures of biological interaction. European Journal of Epidemiology 20: 575–579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Prenatal nitrate intake from drinking water and selected birth defects in offspring of participants in the National Birth Defects Prevention Study. Environmental Health Perspectives 121: 1083–1089.

Rothman, K. J., S. Greenland, and T. L. Lash. 2008. Modern Epidemiology. 3rd ed. Philadelphia: Lippincott Williams & Wilkins.