Wir wollen sehen, wie es funktioniert

Uns liegen vierteljährliche Daten zur Inflation, zur Produktionslücke und zum Leitzins vor.

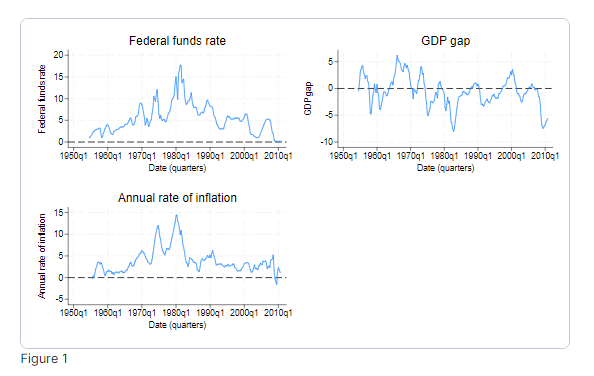
Wir beginnen mit der Schätzung der Impuls-Antwort-Funktion eines univariaten Modells der Produktionslücke.

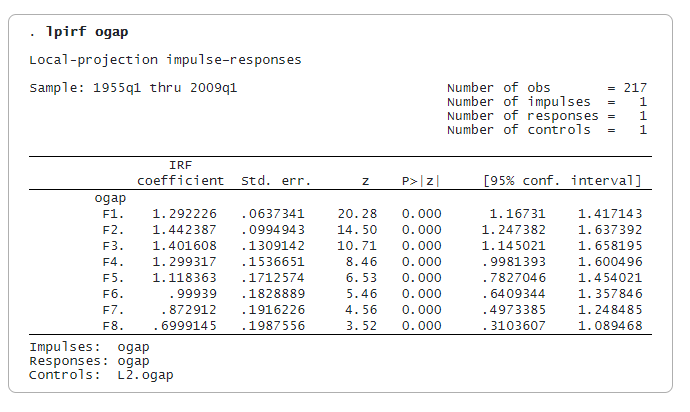
Jeder Koeffizient ist die Reaktion auf einen Impuls (Schock) auf die Produktionslücke in der angegebenen Anzahl von Perioden im Voraus. Beim Aufprall beträgt die Wirkung des Schocks eine Einheit. Nach einer Periode (F1.ogap) steigt die Produktionslücke weiter auf 1,29 an. In der zweiten Periode erreicht sie mit 1,44 ihren Höchststand. Acht Perioden nach einem Schock fällt die Reaktion auf 0,70.

Interessantere Modelle ergeben sich, wenn es mehrere Variablen gibt. In diesem Fall können wir die Auswirkungen eines Schocks auf eine Variable auf eine andere bewerten. Wir kombinieren den Befehl lpirf mit der Befehlssuite irf, um orthogonalisierte Impuls-Antwort-Funktionen zu schätzen und anschließend grafisch darzustellen.

. quietly lpirf inflation ogap fedfunds, lags(1/12) step(24)
. irf set myirfs.irf, replace
. irf create model1
. irf graph oirf, yline(0)

In der ersten Reihe ist die Reaktion auf einen Leitzinsschock dargestellt, in der zweiten Reihe die Reaktion auf einen Inflationsschock und in der letzten Reihe die Reaktion auf einen Produktionslückenschock. Ein unerwarteter Anstieg der Zinssätze führt dazu, dass sowohl die Inflation als auch die Produktion in den folgenden Quartalen zurückgehen, wobei die Reaktion der Inflation etwa 12 Schritte (3 Jahre) nach dem Impuls und die Reaktion der Produktion etwa 8 Schritte (2 Jahre) nach dem Impuls einen Tiefpunkt erreicht. Der Inflationsschock treibt die Inflation und die Produktion in entgegengesetzte Richtungen, und der Zinssatz steigt als Reaktion darauf geringfügig an. Der Produktionsschock führt dazu, dass sowohl die Inflation als auch der Zinssatz ansteigen.

Mal sehen, ob es wieder funktioniert

In diesem Beispiel haben wir einen monatlichen Datensatz über den Logarithmus des Industrieproduktionsindex, den Logarithmus des Verbraucherpreisindex und ein Maß für exogene monetäre Schocks aus Romer und Romer (2004), das in Wieland und Yang (2020) aktualisiert wurde.

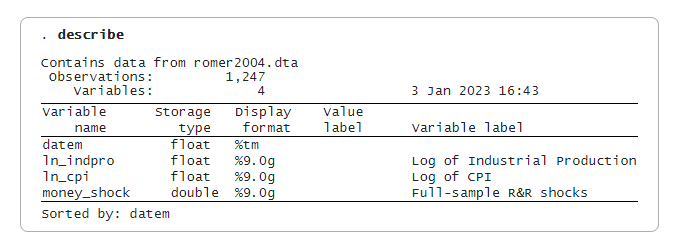
Wir interessieren uns für die Reaktionen der Industrieproduktion und der Inflation auf einen monetären Schock. Wir behandeln Industrieproduktion und Inflation als endogen und den monetären Schock als exogen. Wir passen zwei Modelle an: ein lokales Projektionsmodell und ein Vektorautoregressionsmodell (VAR).

. irf set comparemodels.irf, replace
. quietly lpirf indpro inflation, lags(1/12) exog(L(0/12).money_shock)
. irf create lpmodel
. quietly var indpro inflation, lags(1/12) exog(L(0/12).money_shock)
. irf create varmodel
. irf graph dm, impulse(money_shock) irf(lpmodel varmodel)

Die dynamischen Multiplikatoren aus den Modellen der lokalen Projektion und des VAR sind

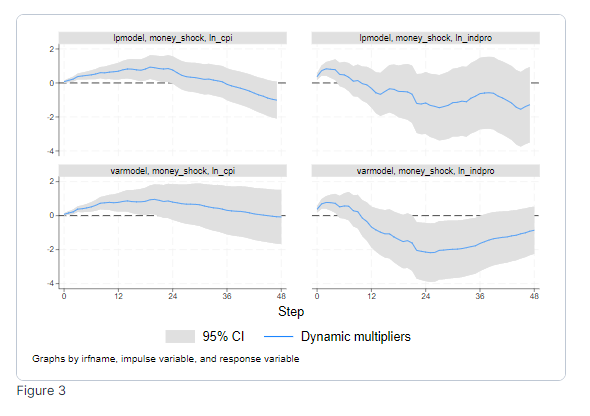
Die obere Zeile zeigt die Ergebnisse des Modells der lokalen Projektion. Die untere Reihe zeigt die Ergebnisse des VAR-Modells, wobei der Geldschock als exogen betrachtet wird.

Sowohl das Modell der lokalen Projektion als auch das VAR-Modell zeigen einen leichten Anstieg des Preisniveaus nach einem monetären Schock, der etwa 24 Monate nach dem Schock seinen Höhepunkt erreicht und danach wieder zurückgeht. Beide Modelle deuten darauf hin, dass die Industrieproduktion nach einem Währungsschock sinkt, wobei der Tiefpunkt etwa 24 Monate nach dem Schock erreicht wird. Die IRFs der lokalen Projektion und die IRFs des VAR-Modells liefern über kurze Zeithorizonte ähnliche Ergebnisse, beginnen jedoch bei längeren Zeithorizonten zu divergieren. Lokale Projektionen bieten mehr Flexibilität bei langfristigen Reaktionen, da sie direkt geschätzt werden. Außerdem sind lokale Projektionen viel schneller zu berechnen.

Referenzen

Romer, C. D., und D. H. Romer. 2004. Ein neues Maß für monetäre Schocks: Ableitung und Implikationen. American Economic Review 94: 1055-1084.

Wieland, J. F., und M. Yang. 2020. Finanzielle Dämpfung. Journal of Money, Credit, and Banking 52: 79-113.