Нека видим как работи

Разполагаме с тримесечни данни за инфлацията, производствената разлика и лихвения процент по федералните фондове.

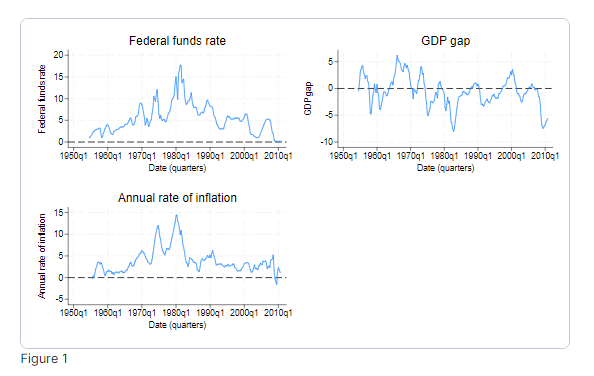
Започваме с оценка на функцията „импулс-реакция“ на едномерния модел на производствената разлика.

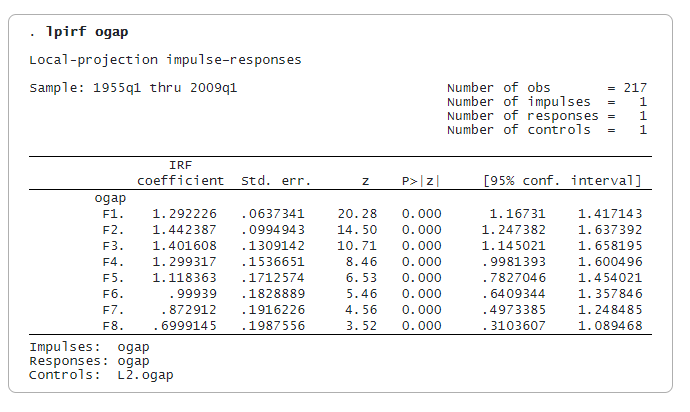
Всеки коефициент е отговорът на импулс (шок) на производствената разлика за определен брой периоди напред. В момента на въздействието ефектът от шока е една единица. След един период (F1.ogap) разликата в производството се увеличава допълнително до 1,29. След това през втория период достига най-високото си равнище от 1,44. Реакцията спада до 0,70 осем периода след шока.

По-интересни модели възникват, когато има множество променливи, като в този случай можем да оценим ефекта от шока върху една променлива върху друга. Комбинираме командата lpirf с набора от команди irf, за да оценим, а след това и да изобразим ортогонизирани функции импулс-реакция.

. quietly lpirf inflation ogap fedfunds, lags(1/12) step(24)
. irf set myirfs.irf, replace
. irf create model1
. irf graph oirf, yline(0)

На първия ред е показана реакцията на шока на лихвения процент по федералните фондове; на втория ред е показана реакцията на шока на инфлацията; а на последния ред е показана реакцията на шока на производствената разлика. Неочакваното покачване на лихвените проценти води до спад на инфлацията и производството през следващите тримесечия, като реакцията на инфлацията достига своя връх около 12 стъпки (3 години) след импулса, а реакцията на производството – около 8 стъпки (2 години) след импулса. Инфлационният шок тласка инфлацията и производството в противоположни посоки, а лихвеният процент се повишава слабо в отговор. Производственият шок води до повишаване и на инфлацията, и на лихвения процент.

Нека да видим как работи отново

В този пример разполагаме с месечен набор от данни за логаритъма на индекса на индустриалното производство, логаритъма на индекса на потребителските цени и мярка за екзогенни парични шокове от Romer и Romer (2004 г.) и актуализирана във Wieland и Yang (2020 г.).

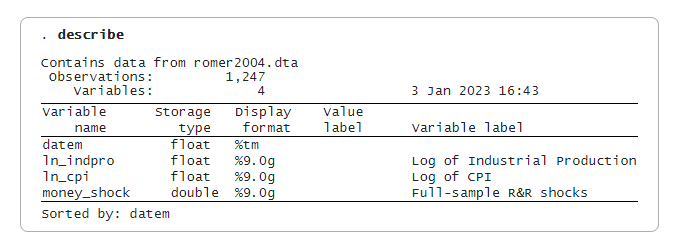
Интересуваме се от реакциите на промишленото производство и инфлацията на паричен шок. Разглеждаме промишленото производство и инфлацията като ендогенни, а паричния шок като екзогенен. Прилагаме два модела: модел на локална проекция и модел на векторна авторегресия (VAR).

. irf set comparemodels.irf, replace
. quietly lpirf indpro inflation, lags(1/12) exog(L(0/12).money_shock)
. irf create lpmodel
. quietly var indpro inflation, lags(1/12) exog(L(0/12).money_shock)
. irf create varmodel
. irf graph dm, impulse(money_shock) irf(lpmodel varmodel)

Динамичните мултипликатори от моделите с локална проекция и VAR са

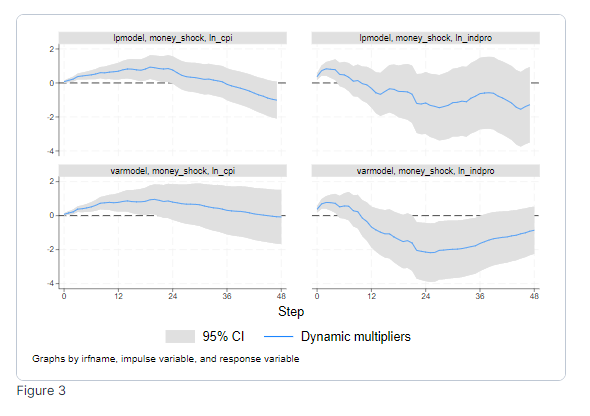
На горния ред са показани резултатите от модела с локална проекция. На долния ред са показани резултатите от модела VAR, при който паричният шок се третира като екзогенен.

Както локалната проекция, така и VAR моделът показват леко нарастване на ценовото равнище след паричен шок, което достига своя връх около 24 месеца след шока и след това намалява. И двата модела показват, че промишленото производство спада след паричен шок, като най-ниската точка се наблюдава около 24 месеца след шока. IRF на локалната проекция и IRF на модела VAR дават сходни резултати в краткосрочен хоризонт, но започват да се разминават в по-дълъг хоризонт. Локалните проекции осигуряват по-голяма гъвкавост на дългосрочните реакции, като ги оценяват директно. Освен това локалните проекции се изчисляват много по-бързо.

Препратки

Romer, C. D. и D. H. Romer. 2004. Нов измерител на паричните шокове: Извод и последици. American Economic Review 94: 1055-1084.

Wieland, J. F., и M. Yang. 2020. Financial dampening. Journal of Money, Credit, and Banking 52: 79-113.