Nou în 
Jupyter Notebook cu Stata
Jupyter Notebook este o aplicație web puternică și ușor de utilizat care vă permite să combinați cod executabil, vizualizări, ecuații și formule matematice, text narativ și alte medii bogate într-un singur document (un „notebook”) pentru calcul interactiv și dezvoltare . Noteboke-urile Jupyter au fost utilizate pe scară largă de cercetători și oameni de știință pentru a-și împărtăși ideile și rezultatele pentru colaborare și inovare.
Acum, puteți invoca Stata și Mata din notebook-urile Jupyter cu kernel-ul IPython (Python interactiv), ceea ce înseamnă că puteți combina atât capabilitățile Python cât și Stata într-un singur mediu pentru a vă face munca ușor reproductibilă și partajabilă cu alții.
Să vedem cum funcționează
În Jupyter Notebook, puteți utiliza două seturi de instrumente furnizate de pachetul pystata Python pentru a interacționa cu Stata:
- Trei comenzi magice IPython (Python interactiv): stata, mata și pystata
- O suită de funcții API
Înainte de a vă arăta cum să utilizați aceste instrumente, configurăm pachetul pystata. Să presupunem că aveți Stata instalat în C: \ Program Files \ Stata17 \ și că utilizați ediția Stata / MP. Stata poate fi inițializată după cum urmează:
In [1]:
import stata_setup
stata_setup.config(„C:/Program Files/Stata17”, „mp”)
Repere
- Invocați Stata din Python
- Stata folosind comenzi magice stata, mata și pystata
- Apelați Stata utilizând o suită de funcții API
- Utilizați comenzile magice și funcțiile API împreună cu modulul Stata Function Interface (sfi)
- Python și Stata împreună
- Accesați Stata și Mata din Jupyter Notebook, Jupyter Lab și din alte medii care acceptă kernel-ul IPython
- Împingeți datele și rezultatele Stata în Python și invers
- Combinați capacitățile Stata și Python într-un singur mediu
___ ____ ____ ____ ____ ©
/__ / ____/ / ____/ 17.0
___/ / /___/ / /___/ MP—Parallel Edition
Statistics and Data Science Copyright 1985-2021 StataCorp LLC
StataCorp
4905 Lakeway Drive
College Station, Texas 77845 USA
800-STATA-PC https://www.stata.com
979-696-4600 stata@stata.com
Stata license: 10-user 4-core network perpetual
Serial number: 1
Licensed to: Stata Developer
StataCorp LLC
Notes:
1. Unicode is supported; see help unicode_advice.
2. More than 2 billion observations are allowed; see help obs_advice.
3. Maximum number of variables is set to 5,000; see help set_maxvar.
.
If you get output similar to what is shown above for your edition of Stata, it means that everything is configured properly; see Configuration for more ways to configure pystata.
Call Stata using magic commands
The stata magic is used to execute Stata commands in an IPython environment. In a notebook cell, we put Stata commands underneath the %%stata cell magic to direct the cell to call Stata. The following commands load the auto dataset and summarize the mpg variable. The Stata output is displayed underneath the cell.
In [2]:
%%stata
sysuse auto, clear
summarize mpg
. sysuse auto, clear
(1978 automobile data)
. summarize mpg
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
mpg | 74 21.2973 5.785503 12 41
.
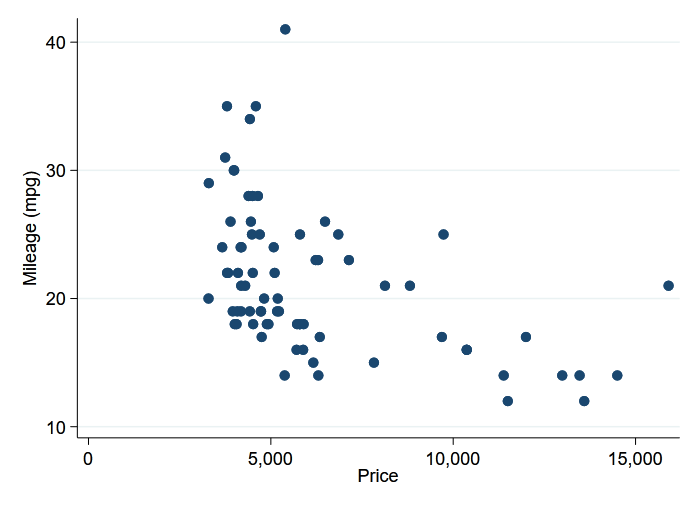
Stata’s graphs can also be displayed in the IPython environment. Here we create a scatterplot of car mileage against price by using the %stata line magic.
In [3]:
%stata scatter mpg price
Apoi, încărcăm datele Python în Stata, efectuăm analize în Stata și apoi transmitem rezultatele returnate Stata către Python pentru analize ulterioare, utilizând al doilea sondaj de examinare națională privind sănătatea și nutriția (NHANES II; McDowell et al 1981).
NHANES II, un set de date privind starea de sănătate și nutrițională a adulților și copiilor din SUA, conține 10.351 de observații și 58 de variabile și este stocat într-un fișier CSV numit nhanes2.csv. Printre aceste variabile se numără o variabilă indicator pentru hipertensiune (highbp) și variabilele continue de vârstă și greutate.
Folosim metoda pandas read_csv () pentru a citi datele din fișierul .csv într-un cadru de date pandas numit nhanes2.
In [4]:
import pandas as pd
import io
import requests
data = requests.get(https://www.stata.com/python/pystata/misc/nhanes2.csv”).content
nhanes2 = pd.read_csv(io.StringIO(data.decode(„utf-8”)))
nhanes2
Out [4]:
Încărcăm cadrul de date în Stata specificând argumentul -d al magiei %%stata, iar apoi în Stata, potrivim un model de regresie logistică folosind vârsta, greutatea și interacțiunea lor ca predictori ai probabilității de hipertensiune. De asemenea, împingem rezultatele estimărilor Stata afișate prin lista de revenire, inclusiv vectorul coeficientului e(b) și matricea varianță – covarianță e(V), într-un dicționar Python numit myeret prin specificarea argumentului -eret.
In [5]:
%%stata -d nhanes2 -eret myeret
logistic highbp c.age##c.weight
ereturn list
. logistic highbp c.age##c.weight
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
. ereturn list
scalars:
e(rank) = 4
e(N) = 10351
e(ic) = 4
e(k) = 4
e(k_eq) = 1
e(k_dv) = 1
e(converged) = 1
e(rc) = 0
e(ll) = -5860.151218806021
e(k_eq_model) = 1
e(ll_0) = -7050.765484416371
e(df_m) = 3
e(chi2) = 2381.2285312207
e(p) = 0
e(N_cdf) = 0
e(N_cds) = 0
e(r2_p) = .1688631210670459
macros:
e(cmdline) : "logistic highbp c.age##c.weight"
e(cmd) : "logistic"
e(predict) : "logistic_p"
e(estat_cmd) : "logit_estat"
e(marginsok) : "default Pr"
e(marginsnotok) : "stdp DBeta DEviance DX2 DDeviance Hat Number Resi.."
e(title) : "Logistic regression"
e(chi2type) : "LR"
e(opt) : "moptimize"
e(vce) : "oim"
e(user) : "mopt__logit_d2()"
e(ml_method) : "d2"
e(technique) : "nr"
e(which) : "max"
e(depvar) : "highbp"
e(properties) : "b V"
matrices:
e(b) : 1 x 4
e(V) : 4 x 4
e(mns) : 1 x 4
e(rules) : 1 x 4
e(ilog) : 1 x 20
e(gradient) : 1 x 4
functions:
e(sample)
.
Putem accesa e(b) și e(V) tastând myeret [‘e (b)’] și respectiv myeret [‘e (V)’], în Python. Acestea sunt stocate în tablourile NumPy.
In [6]:
myeret [‘e(b)’], myeret[‘e(V)’]
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Folosim marjele și graficul marjelor pentru a realiza graficul predicțiilor pentru vârstă, ceea ce ilustrează mai clar relația dintre vârstă și probabilitatea hipertensiunii.
In [7]:
%%stata
quietly margins, at(age=(20(10)80))
marginsplot
. quietly margins, at(age=(20(10)80)) . marginsplot Variables that uniquely identify margins: age .

Folosim margini pentru a estima probabilitatea de hipertensiune estimată pentru toate combinațiile de vârstă și greutate pentru valori de vârstă cuprinse între 20 și 80 de ani în trepte de 5 și pentru valori de greutate cuprinse între 40 și 180 de kilograme în trepte de 5. Opțiunea de salvare(predicții, înlocuire) salvează predicțiile într-un set de date numit predictions.dta. Scopul nostru este să folosim Python pentru a crea un grafic de suprafață tridimensional cu aceste predicții.
Setul de date predictions.dta conține variabilele _at1 și _at2, care corespund valorilor de vârstă și greutate pe care le-am specificat în opțiunea at (). Setul de date conține, de asemenea, variabila _margin, care este predicția marginală a probabilității tensiunii arteriale crescute. Redenumim acele variabile ca vârstă, greutate și respectiv pr_highbp.
În cele din urmă, stocăm setul de date în Stata ca un cadru de date pandas numit preddata în Python prin specificarea argumentului -doutd.
In [8]:
%%stata -doutd preddata
quietly margins, at(age=(20(5)80) weight=(40(5)180))
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
Enumerăm primele cinci observații ale coloanelor de vârstă, greutate, pr_highbp din cadrul de date.
In [9]:
preddata[[‘age’, ‘weight’, ‘pr_highbp’]].head()
Out [9]:
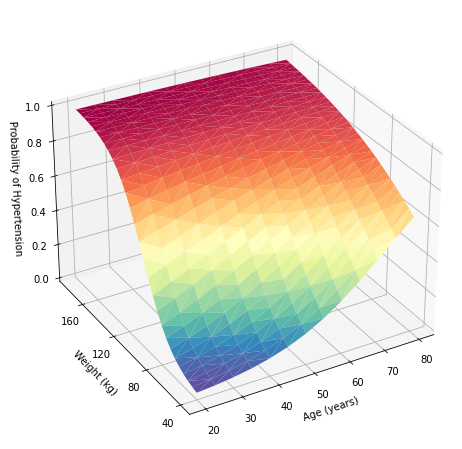
Next we use Python to create a three-dimensional surface plot. First, we set the graph size to be 10 by 8 inches using the figure() method in the pyplot module of the Matplotlib package. We use the axes() method to define a three-dimensional set of axes named ax and draw the surfrace plot with the plot_trisurf() method. Next we set the ticks and labels for the x, y, and z axes. Last, we adjust the elevation and azimuth of the plot.
In [11]:
import matplotlib.pyplot as plt
import numpy as np
# define the axes
fig = plt.figure(1, figsize=(10, 8))
ax = plt.axes(projection=‘3d’)
# plot
ax.plot_trisurf(preddata[‘age’], preddata[‘weight’], preddata[‘pr_highbp’],cmap=plt.cm.Spectral_r)
# set ticks and labels for x, y, and z axes
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_xlabel(Age (years)”)
ax.set_ylabel(Weight (kg)”)
ax.set_zlabel(Probability of Hypertension”)
# adjust the view angle
ax.view_init(elev=30, azim=240)
# show the plot
plt.show()
Interacționați cu Stata folosind funcțiile API
De asemenea, putem interacționa cu Stata folosind o suită de funcții definite în modulele config și stata din pachetul pystata Python. Vom demonstra cum să utilizați aceste funcții API pentru a interacționa cu Stata ca alternativă la comanda magică %%stata.
Importăm modulul stata din pystata. Apoi, apelați metoda pdataframe_to_data() pentru a încărca pandas dataframe nhanes2 în Stata și apelați metoda run() pentru a se potrivi modelului de regresie logistică
In [12]:
from pystata import
stata
stata.pdataframe_to_data(nhanes2, force=True)
stata.run(‘logistic highbp c.age##c.weight’)
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
Apoi folosim metoda get_ereturn() pentru a stoca rezultatele e() returnate de comanda logistică în Python ca un dicționar numit myeret2 și afișăm în ea e(b) și e(V).
In [13]:
myeret2 = stata.get_ereturn()
myeret2[‘e(b)’], myeret2[‘e(V)’]
Out [13]:
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Next we call the run() method to estimate the predicted probability of hypertension for all combinations of age and weight, save the prediction results in a dataset named predictions.data, and load the dataset into Stata and rename the variables.
In [14]:
stata.run(”’
quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
”’)
.
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
We call the pdataframe_from_data() function in the stata module to store the age, weight, and pr_highbp in current dataset to a pandas dataframe named preddata2.
In [15]:
preddata2 = stata.pdataframe_from_data(var=„age weight pr_highbp”)
preddata2.head()
Out [15]:
Once we have this dataframe, we can create the same three-dimensional surface plot as above.
Note that you can also use the Stata Function Interface (sfi) module to access Stata’s core features. The combination of those tools makes it much easier to interact with Stata from Jupyter Notebook; see Example 5: Call Stata using API functions for an example.
Referințe
Hunter, J. D. 2007. Matplotlib: Un mediu grafic 2D. Calcul în știință și inginerie 9: 90-95.
McDowell, A., A. Engel, J. T. Massey și K. Maurer. 1981. Planul și funcționarea celui de-al doilea sondaj național de examinare a sănătății și nutriției, 1976–1980. Statistici vitale și de sănătate 1 (15): 1–144.
Mckinney, W. 2010. Structuri de date pentru calculul statistic în Python. Lucrările celei de-a 9-a conferințe Python in Știință, 56-61. (linkul editorului).
Oliphant, T. E. 2006. A Guide to NumPy, 2nd ed. Austin, TX: Continuum Press. Oliphant, T. E. 2006. Un ghid pentru NumPy, ed. A 2-a. Austin, TX: Continuum Press.
Péz, F. și B. E. Granger. 2007. IPython: Calcul științific interactiv, calcul în Știință și Inginerie 9: 21-29. DOI: 10.1109 / MCSE.2007.53 (link editor)
