Nouveau dans 
Jupyter Notebook avec Stata
Jupyter Notebook est une application web puissante et facile à utiliser qui vous permet de combiner du code exécutable, des visualisations, des équations et formules mathématiques, du texte narratif et d’autres médias riches dans un seul document (un « notebook ») pour le calcul et le développement interactifs. Les carnets Jupyter ont été largement utilisés par les chercheurs et les scientifiques pour partager leurs idées et leurs résultats à des fins de collaboration et d’innovation.
Désormais, vous pouvez invoquer Stata et Mata à partir de Jupyter Notebooks avec le noyau IPython (Python interactif), ce qui signifie que vous pouvez combiner les capacités de Python et de Stata dans un seul environnement pour rendre votre travail facilement reproductible et partageable avec d’autres.
Voyons comment cela fonctionne
Dans Jupyter Notebook, vous pouvez utiliser deux ensembles d’outils fournis par le paquetage Python pystata pour interagir avec Stata:
- 1.Trois commandes magiques IPython (Python interactif): stata, mata et pystata.
- 2.Une suite de fonctions API
Avant de vous montrer comment utiliser ces outils, nous allons configurer le paquetage pystata. Supposons que vous ayez installé Stata dans C:\Program Files\Stata17\ et que vous utilisiez l’édition Stata/MP. Stata peut être initialisé comme suit:
Sur [1]:
In [1]:
import stata_setup
stata_setup.config(« C:/Program Files/Stata17 », « mp »)
Points forts
- Appeler Stata à partir de Python
- Appeler Stata à l’aide des commandes magiques stata, mata et pystata
- Appeler Stata à l’aide d’une suite de fonctions API
- Utilisez les commandes magiques et les fonctions API avec le module Stata Function Interface (sfi).
- Utilisez Python et Stata ensemble
- Accédez à Stata et Mata depuis Jupyter Notebook, Jupyter Lab et d’autres environnements qui supportent le noyau IPython.
- Transférez les données et les résultats de Stata vers Python et vice versa.
- Combinez les capacités de Stata et de Python dans un seul environnement.
___ ____ ____ ____ ____ ©
/__ / ____/ / ____/ 17.0
___/ / /___/ / /___/ MP—Parallel Edition
Statistics and Data Science Copyright 1985-2021 StataCorp LLC
StataCorp
4905 Lakeway Drive
College Station, Texas 77845 USA
800-STATA-PC https://www.stata.com
979-696-4600 stata@stata.com
Stata license: 10-user 4-core network perpetual
Serial number: 1
Licensed to: Stata Developer
StataCorp LLC
Notes:
1. Unicode is supported; see help unicode_advice.
2. More than 2 billion observations are allowed; see help obs_advice.
3. Maximum number of variables is set to 5,000; see help set_maxvar.
.
Si vous obtenez un résultat similaire à celui indiqué ci-dessus pour votre édition de Stata, cela signifie que tout est configuré correctement; voir Configuration pour plus de moyens de configurer pystata..
Appeler Stata en utilisant des commandes magiques
La magie stata est utilisée pour exécuter des commandes Stata dans un environnement IPython. Dans une cellule de bloc-notes, nous plaçons les commandes Stata sous la magie %%stata cell pour demander à la cellule d’appeler Stata. Les commandes suivantes chargent l’ensemble de données auto et résument la variable mpg. La sortie Stata est affichée sous la cellule.
Sur [2]:
%%stata
sysuse auto, clear
summarize mpg
. sysuse auto, clear
(1978 automobile data)
. summarize mpg
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
mpg | 74 21.2973 5.785503 12 41
.
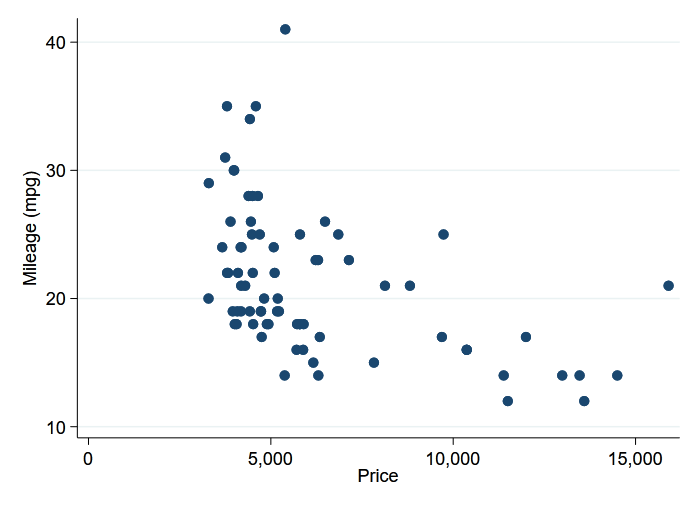
Les graphiques de Stata peuvent également être affichés dans l’environnement IPython. Ici, nous créons un nuage de points du kilométrage des voitures en fonction du prix en utilisant la magie de la ligne %stata..
Sur [3]:
%stata scatter mpg price
Ensuite, nous chargeons les données Python dans Stata, effectuons les analyses dans Stata, puis transmettons les résultats retournés par Stata à Python pour une analyse plus approfondie, en utilisant la deuxième enquête nationale sur la santé et la nutrition (NHANES II; McDowell et al. 1981).
NHANES II, un ensemble de données concernant la santé et l’état nutritionnel des adultes et des enfants aux États-Unis, contient 10 351 observations et 58 variables et est stocké dans un fichier CSV appelé nhanes2.csv. Parmi ces variables, on trouve une variable indicatrice d’hypertension (highbp) et les variables continues âge et poids.
Nous utilisons la méthode pandas read_csv() pour lire les données du fichier .csv dans un cadre de données pandas nommé nhanes2.
Sur [4]:
import pandas as pd
import io
import requests
data = requests.get(https://www.stata.com/python/pystata/misc/nhanes2.csv »).content
nhanes2 = pd.read_csv(io.StringIO(data.decode(« utf-8 »)))
nhanes2
Out [4]:
Nous chargeons le cadre de données dans Stata en spécifiant l’argument -d de la magie %%stata, and puis dans Stata, nous ajustons un modèle de régression logistique en utilisant l’âge, le poids, et leur interaction comme prédicteurs de la probabilité d’hypertension. Nous poussons également les résultats d’estimation de Stata affichés par ereturn list, y compris le vecteur de coefficient e(b) et la matrice de variance-covariance e(V), dans un dictionnaire Python appelé myeret en spécifiant l’argument -eret.
In [5]:
%%stata -d nhanes2 -eret myeret
logistic highbp c.age##c.weight
ereturn list
. logistic highbp c.age##c.weight
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
. ereturn list
scalars:
e(rank) = 4
e(N) = 10351
e(ic) = 4
e(k) = 4
e(k_eq) = 1
e(k_dv) = 1
e(converged) = 1
e(rc) = 0
e(ll) = -5860.151218806021
e(k_eq_model) = 1
e(ll_0) = -7050.765484416371
e(df_m) = 3
e(chi2) = 2381.2285312207
e(p) = 0
e(N_cdf) = 0
e(N_cds) = 0
e(r2_p) = .1688631210670459
macros:
e(cmdline) : "logistic highbp c.age##c.weight"
e(cmd) : "logistic"
e(predict) : "logistic_p"
e(estat_cmd) : "logit_estat"
e(marginsok) : "default Pr"
e(marginsnotok) : "stdp DBeta DEviance DX2 DDeviance Hat Number Resi.."
e(title) : "Logistic regression"
e(chi2type) : "LR"
e(opt) : "moptimize"
e(vce) : "oim"
e(user) : "mopt__logit_d2()"
e(ml_method) : "d2"
e(technique) : "nr"
e(which) : "max"
e(depvar) : "highbp"
e(properties) : "b V"
matrices:
e(b) : 1 x 4
e(V) : 4 x 4
e(mns) : 1 x 4
e(rules) : 1 x 4
e(ilog) : 1 x 20
e(gradient) : 1 x 4
functions:
e(sample)
.
Nous pouvons accéder à e(b) et e(V) en tapant myeret[‘e(b)’] et myeret[‘e(V)’], respectivement, en Python. Ils sont stockés dans des tableaux NumPy.
In [6]:
myeret [‘e(b)’], myeret[‘e(V)’]
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Nous utilisons margins et marginsplot pour représenter graphiquement les prédictions en fonction de l’âge, ce qui illustre plus clairement la relation entre l’âge et la probabilité d’hypertension.
Sur [7]:
%%stata
quietly margins, at(age=(20(10)80))
marginsplot
. quietly margins, at(age=(20(10)80)) . marginsplot Variables that uniquely identify margins: age .

Nous utilisons les marges pour estimer la probabilité prédite d’hypertension pour toutes les combinaisons d’âge et de poids pour des valeurs d’âge pour des valeurs d’âge allant de 20 à 80 ans par incréments de 5 et pour des valeurs de poids allant de 40 à 180 kilogrammes par incréments de 5. L’option saving(predictions, replace) enregistre les prédictions dans un jeu de données nommé predictions.dta. Notre objectif est d’utiliser Python pour créer un tracé de surface tridimensionnel de ces prédictions.
Le jeu de données predictions.dta contient les variables _at1 et _at2, qui correspondent aux valeurs d’âge et de poids que nous avons spécifiées dans l’option at(). Le jeu de données contient également la variable _margin, qui est la prédiction marginale de la probabilité d’hypertension artérielle. Nous renommons ces variables en âge, poids, et pr_highbp respectivement.
Enfin, nous stockons l’ensemble de données dans Stata sous la forme d’un dataframe pandas nommé preddata en Python en spécifiant l’argument -doutd.
In [8]:
%%stata -doutd preddata
quietly margins, at(age=(20(5)80) weight=(40(5)180))
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
Nous listons les cinq premières observations des colonnes âge, poids, pr_highbp dans le cadre de données.
Sur [9]:
preddata[[‘age’, ‘weight’, ‘pr_highbp’]].head()
Out [9]:
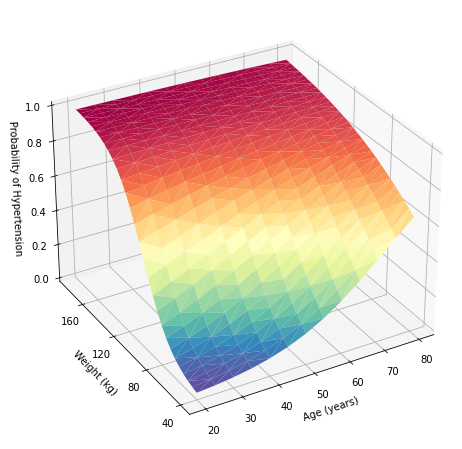
Ensuite, nous utilisons Python pour créer un graphique de surface tridimensionnel. Tout d’abord, nous définissons la taille du graphique (10 x 8 pouces) à l’aide de la méthode figure() du module pyplot du paquetage Matplotlib. Nous utilisons la méthode axes() pour définir un ensemble tridimensionnel d’axes nommés ax et nous dessinons le tracé surfacique avec la méthode plot_trisurf() Ensuite, nous définissons les ticks et les étiquettes pour les axes x, y et z. Enfin, nous ajustons l’élévation et l’azimut du tracé.
In [11]:
import matplotlib.pyplot as plt
import numpy as np
# define the axes
fig = plt.figure(1, figsize=(10, 8))
ax = plt.axes(projection=‘3d’)
# plot
ax.plot_trisurf(preddata[‘age’], preddata[‘weight’], preddata[‘pr_highbp’],cmap=plt.cm.Spectral_r)
# set ticks and labels for x, y, and z axes
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_xlabel(Age (years) »)
ax.set_ylabel(Weight (kg) »)
ax.set_zlabel(Probability of Hypertension »)
# adjust the view angle
ax.view_init(elev=30, azim=240)
# show the plot
plt.show()
Interagir avec Stata en utilisant les fonctions API
Nous pouvons également interagir avec Stata en utilisant une suite de fonctions définies dans les modules config et stata du paquetage Python pystata. Nous allons démontrer comment utiliser ces fonctions API pour interagir avec Stata comme alternative à la commande magique %%stata.
Nous importons le module stata de pystata. Nous appelons ensuite la méthode pdataframe_to_data() pour charger le dataframe pandas nhanes2 dans Stata et appelons la méthode run() pour ajuster le modèle de régression logistique.
Sur [12]:
from pystata import
stata
stata.pdataframe_to_data(nhanes2, force=True)
stata.run(‘logistic highbp c.age##c.weight’)
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
Ensuite, nous utilisons la méthode get_ereturn() pour stocker les résultats e() renvoyés par la commande logistique en Python dans un dictionnaire nommé myeret2 et y afficher e(b) et e(V).
Sur [13]:
myeret2 = stata.get_ereturn()
myeret2[‘e(b)’], myeret2[‘e(V)’]
Out [13]:
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Ensuite, nous appelons la méthode run() pour estimer la probabilité prédite d’hypertension pour toutes les combinaisons d’âge et de poids, nous sauvegardons les résultats de la prédiction dans un ensemble de données nommé predictions.data, nous chargeons l’ensemble de données dans Stata et nous renommons les variables.
Sur [14]:
stata.run( »’
quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
»’)
.
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
Nous appelons la fonction pdataframe_from_data() du module stata pour stocker l’âge, le poids, et le pr_highbp de l’ensemble de données actuel dans un dataframe pandas nommé preddata2.
In [15]:
preddata2 = stata.pdataframe_from_data(var=« age weight pr_highbp »)
preddata2.head()
Out [15]:
Une fois que nous disposons de ce cadre de données, nous pouvons créer le même graphique de surface tridimensionnel que ci-dessus.
Notez que vous pouvez également utiliser le module Stata Function Interface (sfi) pour accéder aux fonctionnalités de base de Stata. La combinaison de ces outils facilite grandement l’interaction avec Stata à partir de Jupyter Notebook ; voir l’exemple 5 : Appeler Stata à l’aide des fonctions API pour un exemple.
Références
Hunter, J. D. 2007. Matplotlib : A 2D Graphics Environment. Computing in Science & Engineering 9 : 90-95.
McDowell, A., A. Engel, J. T. Massey, et K. Maurer. 1981. Plan et fonctionnement de la deuxième enquête nationale sur la santé et la nutrition, 1976-1980. Vital and Health Statistics 1(15) : 1-144.
Mckinney, W. 2010. Structures de données pour le calcul statistique en Python. Actes de la 9e conférence Python in Science, 56-61. (lien éditeur).
Oliphant, T. E. 2006. A Guide to NumPy, 2e édition. Austin, TX : Continuum Press.
Péz, F., et B. E. Granger. 2007. IPython : A System for Interactive Scientific Computing, Computing in Science and Engineering 9 : 21-29. DOI:10.1109/MCSE.2007.53 (lien éditeur)
