Újdonságok a  -ben
-ben
Jupyter Notebook a Stata-val
A Jupyter Notebook egy hatékony és könnyen használható webalkalmazás, amely lehetővé teszi a futtatható kód, a vizualizációk, a matematikai egyenletek és képletek, az elbeszélő szöveg és az egyéb gazdag adathordozók egyetlen dokumentumban („notebook”) történő összekapcsolását az interaktív számításhoz és fejlesztéshez. A kutatók és tudósok széles körben használták a Jupyter jegyzetfüzeteket, hogy megosszák ötleteiket és eredményeiket az együttműködés és az innováció terén.
Most meghívhatja a Stata és Mata alkalmazásokat a Jupyter Notebooks alkalmazásból az IPython (interaktív Python) kernellel, vagyis a Python és a Stata képességeit egyetlen környezetben egyesítheti, hogy munkája könnyen reprodukálható és megosztható legyen másokkal.
Nézzük hogyan mükődik
A Jupyter Notebook alkalmazásban a pystata Python csomag két eszközkészletét használhatja a Statával való interakcióhoz:
- három IPython (interactive Python) varázsparancs: stata, mata, és pystata
- API funkciók készlete
Mielőtt bemutatnánk, hogyan kell használni ezeket az eszközöket, konfiguráljuk a
pystata csomagot. Tegyük fel, hogy a Stata telepítve vana C:\Program Files\Stata17\ és Ön a Stata/MP kiadást használja. Stata a következőképpen inicializálható:
In [1]:
import stata_setup
stata_setup.config(“C:/Program Files/Stata17”, “mp”)
Kiemelt
- Stata meghívása a Python-ból
- Hívja a Statát stata, mata és pystata varázsparancsokkal
- Hívja a Stata meghívását a PythonStata-ból egy API-függvénykészlet használatával
- Használja a varázsparancsokat és az API funkciókat a Stata Function Interface (sfi) modullal együtt
- Használja a Python-t és a Stata-t együtt
- A Stata és a Mata elérése a Jupyter Notebook, a Jupyter Lab és más olyan környezetekből, amelyek támogatják az IPython kernelt
- A Stata adatokat és eredményeket helyezze a Pythonba és fordítva
- Kombinálja a Stata és a Python képességeit egyetlen környezetben
___ ____ ____ ____ ____ ©
/__ / ____/ / ____/ 17.0
___/ / /___/ / /___/ MP—Parallel Edition
Statistics and Data Science Copyright 1985-2021 StataCorp LLC
StataCorp
4905 Lakeway Drive
College Station, Texas 77845 USA
800-STATA-PC https://www.stata.com
979-696-4600 stata@stata.com
Stata license: 10-user 4-core network perpetual
Serial number: 1
Licensed to: Stata Developer
StataCorp LLC
Notes:
1. Unicode is supported; see help unicode_advice.
2. More than 2 billion observations are allowed; see help obs_advice.
3. Maximum number of variables is set to 5,000; see help set_maxvar.
.
Ha hasonló kimenetet kap, mint amit fent bemutattunk a Stata kiadásnál, ez azt jelenti, hogy minden megfelelően van konfigurálva; A konfigurálás további módjait lásd a Konfiguráció részben pystata.
Varázsparancsok segítségével hívja meg a Statát
A stata varázs a Stata parancsok IPython környezetben történő végrehajtására szolgál. Egy notebook cellába a %%stata cell varázs alá helyezzük a Stata parancsokat, hogy a cellát a Stata hívására irányítsuk. A következő parancsok betöltik az auto adatkészletet, és összefoglalják az mpg változót. A Stata kimenet a cella alatt jelenik meg.
In [2]:
%%stata
sysuse auto, clear
summarize mpg
. sysuse auto, clear
(1978 automobile data)
. summarize mpg
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
mpg | 74 21.2973 5.785503 12 41
.
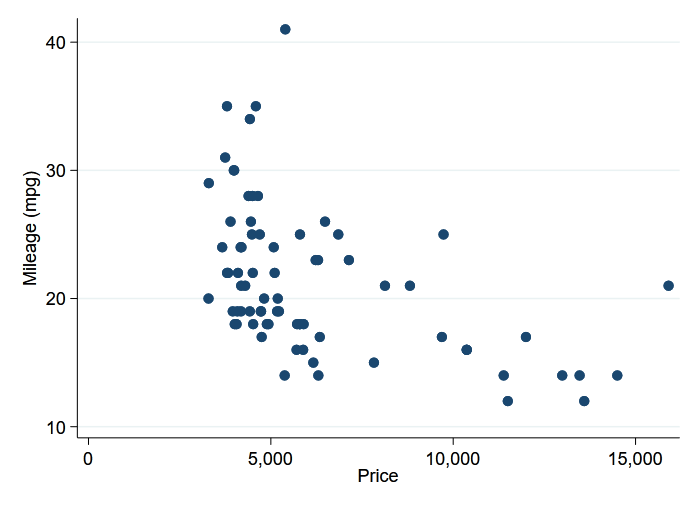
A Stata grafikonjai az IPython környezetben is megjeleníthetők. Itt készítünk egy szórtáblát az autó futásteljesítményéről az ár és a %stata line varázs felhasználásával.
In [3]:
%stata scatter mpg price
Ezután betöltjük a Python adatait a Statába, elemzéseket hajtunk végre a Stata-ban, majd a Stata visszaküldött eredményeit továbbadjuk a Pythonnak további elemzés céljából, a második Nemzeti Egészségügyi és Táplálkozási Vizsgálat segítségével. (NHANES II; McDowell et al. 1981).
A NHANES II, az Egyesült Államokban a felnőttek és gyermekek egészségi és táplálkozási állapotáról szóló adatkészlet 10 351 megfigyelést és 58 változót tartalmaz, és egy nhanes2.csv nevű CSV fájlban van tárolva. Ezen változók között szerepel a hipertónia (highbp) , valamint a folyamatos változók age és a weight. mutatója.
A read_csv() -ból pandas módszerrel olvassuk le az adatokat a .csv fájlból egy nhanes2 nevű pandas adathalmazba.
In [4]:
import pandas as pd
import io
import requests
data = requests.get(https://www.stata.com/python/pystata/misc/nhanes2.csv”).content
nhanes2 = pd.read_csv(io.StringIO(data.decode(“utf-8”)))
nhanes2
Out [4]:
Az adatkeretet a Stata-ba töltjük be a %%stata varázslat -d argumentumának megadásával, majd a Stata-n belül egy logisztikai regressziós modellt illesztünk az age, weight, és az interakció felhasználásával a hipertónia valószínűségének előrejelzőjeként.
A Stata becslési eredményeit az ereturn list, alapján, beleértve az e(b) együtthatóvektort és a variancia – kovariancia mátrixot e(V), is, az -eret argumentum megadásával a myeret nevű Python szótárba toljuk.
In [5]:
%%stata -d nhanes2 -eret myeret
logistic highbp c.age##c.weight
ereturn list
. logistic highbp c.age##c.weight
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
. ereturn list
scalars:
e(rank) = 4
e(N) = 10351
e(ic) = 4
e(k) = 4
e(k_eq) = 1
e(k_dv) = 1
e(converged) = 1
e(rc) = 0
e(ll) = -5860.151218806021
e(k_eq_model) = 1
e(ll_0) = -7050.765484416371
e(df_m) = 3
e(chi2) = 2381.2285312207
e(p) = 0
e(N_cdf) = 0
e(N_cds) = 0
e(r2_p) = .1688631210670459
macros:
e(cmdline) : "logistic highbp c.age##c.weight"
e(cmd) : "logistic"
e(predict) : "logistic_p"
e(estat_cmd) : "logit_estat"
e(marginsok) : "default Pr"
e(marginsnotok) : "stdp DBeta DEviance DX2 DDeviance Hat Number Resi.."
e(title) : "Logistic regression"
e(chi2type) : "LR"
e(opt) : "moptimize"
e(vce) : "oim"
e(user) : "mopt__logit_d2()"
e(ml_method) : "d2"
e(technique) : "nr"
e(which) : "max"
e(depvar) : "highbp"
e(properties) : "b V"
matrices:
e(b) : 1 x 4
e(V) : 4 x 4
e(mns) : 1 x 4
e(rules) : 1 x 4
e(ilog) : 1 x 20
e(gradient) : 1 x 4
functions:
e(sample)
.
Az e(b) és az e e(V) fájlokhoz úgy férhetünk hozzá, hogy a myeret [’e (b)’] és a myeret [’e (V)’] parancsokat beírjuk Pythonba
A NumPy tömbökben vannak tárolva.
In [6]:
myeret [‘e(b)’], myeret[‘e(V)’]
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Az age, előrejelzések ábrázolásához margókat és margótáblát használunk, amelyek egyértelműbben szemléltetik az age és a hipertónia valószínűsége közötti kapcsolatot.
In [7]:
%%stata
quietly margins, at(age=(20(10)80))
marginsplot
. quietly margins, at(age=(20(10)80)) . marginsplot Variables that uniquely identify margins: age .

Margókkal becsüljük meg a magas vérnyomás előrejelzett valószínűségét az age és a weight összes kombinációja esetében a 20 és 80 age közötti értékek esetében 5-ös lépésekben és a weight 40–180 kilogramm közötti értékek esetében szintén 5-ös lépéseket használunk. A saving(predictions, replace) elmenti az előrejelzéseket a predictions.dta. adatállományba. Célunk, hogy a Python segítségével elkészítsük ezeknek az előrejelzéseknek a háromdimenziós felületi diagramját.
Az predictions.dta adatkészlet az _at1 és _at2, változót tartalmazza, amelyek megfelelnek az age és weight értékeinek, amelyeket az at() opcióban adtunk meg. Az adatkészlet tartalmazza a _margin, változót is, amely a magas vérnyomás valószínűségének marginális előrejelzése. Nevezzük át azokat a változóka age, weight, és pr_highbp .
Végül az adathalmazt a Stata-ban preddata nevű pandas adatkeretként tároljuk a Pythonban az -doutd argumentum megadásával.
In [8]:
%%stata -doutd preddata
quietly margins, at(age=(20(5)80) weight=(40(5)180))
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
Felsoroljuk az age, weight, pr_highbp oszlopok első öt megfigyelését az adathalmazon belül.
In [9]:
preddata[[‘age’, ‘weight’, ‘pr_highbp’]].head()
Out [9]:
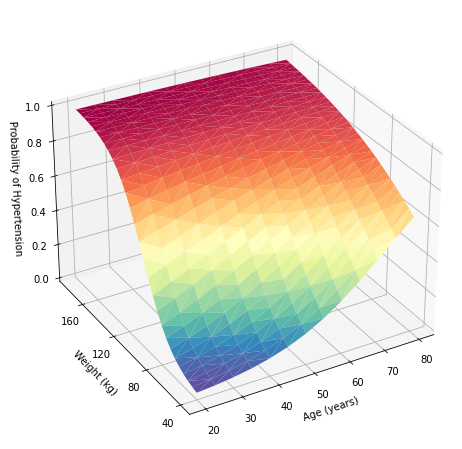
Ezután a Python segítségével létrehozunk egy háromdimenziós felületi ábrát. Először állítsuk be a grafikon méretét 10×8 hüvelykre a Matplotlib csomag pyplot moduljában található figure() módszerrel. Az axes() módszerrel meghatározzuk az ax nevű tengelyek háromdimenziós halmazát, és a plot_trisurf() metódussal megrajzoljuk a felületfelrajzot. Ezután beállítjuk az x, y és z tengely tick-jeit és címkéit. Végül beállítjuk a cselekmény magasságát és azimutját.
In [11]:
import matplotlib.pyplot as plt
import numpy as np
# define the axes
fig = plt.figure(1, figsize=(10, 8))
ax = plt.axes(projection=‘3d’)
# plot
ax.plot_trisurf(preddata[‘age’], preddata[‘weight’], preddata[‘pr_highbp’],cmap=plt.cm.Spectral_r)
# set ticks and labels for x, y, and z axes
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_xlabel(Age (years)”)
ax.set_ylabel(Weight (kg)”)
ax.set_zlabel(Probability of Hypertension”)
# adjust the view angle
ax.view_init(elev=30, azim=240)
# show the plot
plt.show()
Interakció a Statával az API funkciók használatával
A Statával interakcióba léphetünk a pystata Python csomag konfig és stata moduljaiban definiált funkciók használatával is. Bemutatjuk, hogyan lehet ezeket az API-funkciókat használni a Stata-val való interakcióra a %%stata varázsparancs alternatívájaként.
A stata modult a pystata. -ból importáljuk. Ezután hívja meg a pdataframe_to_data () metódust a pandas dataframe nhanes2 Stata-ba való betöltéséhez, és hívja meg a run() metódust, hogy illeszkedjen a logisztikai regressziós modellhez.
In [12]:
from pystata import
stata
stata.pdataframe_to_data(nhanes2, force=True)
stata.run(‘logistic highbp c.age##c.weight’)
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
Ezután a get_ereturn () metódussal tároljuk a Python logistic parancs által visszaadott e() eredményeit myeret2 nevű szótárként, és megjelenítjük benne az e(b) és az e(V) szavakat.
In [13]:
myeret2 = stata.get_ereturn()
myeret2[‘e(b)’], myeret2[‘e(V)’]
Out [13]:
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Ezután a run () metódust hívjuk meg a hipertónia előrejelzett valószínűségének becsléséhez az életkor és a súly összes kombinációjára, az előrejelzési eredményeket elmentjük egy prediktív névre keresztelt adatkészletbe, és betöltjük az adatállományt a Statába, és átnevezzük a változókat.
In [14]:
stata.run(”’
quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
”’)
.
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
A stata modulban a pdataframe_from_data () funkciót meghívjuk az age, súly és pr_highbp aktuális adatkészletben történő tárolására egy preddata2 nevű pandas adathalmazba.
In [15]:
preddata2 = stata.pdataframe_from_data(var=“age weight pr_highbp”)
preddata2.head()
Out [15]:
Miután megvan ez az adatkeret, létrehozhatjuk ugyanazt a háromdimenziós felületi diagramot, mint fent.
Ne feledje, hogy a Stata Function Interface (sfi) modult is használhatja a Stata alapvető szolgáltatásainak eléréséhez.
Ezen eszközök kombinációja sokkal könnyebbé teszi a Jupyter Notebook Stata-val való kapcsolatát; lásd az 5. példát: Hívja a Statát az API funkciók segítségével.
Referenciák
Hunter, J. D. 2007. Matplotlib: A 2D Graphics Environment. Computing in Science & Engineering 9: 90–95.
McDowell, A., A. Engel, J. T. Massey, and K. Maurer. 1981. Plan and operation of the Second National Health and Nutrition Examination Survey, 1976–1980. Vital and Health Statistics 1(15): 1–144.
Mckinney, W. 2010. Data Structures for Statistical Computing in Python. Proceedings of the 9th Python in Science Conference, 56–61. (publisher link).
Oliphant, T. E. 2006. A Guide to NumPy, 2nd ed. Austin, TX: Continuum Press.
Péz, F., and B. E. Granger. 2007. IPython: A System for Interactive Scientific Computing, Computing in Science and Engineering 9: 21–29. DOI:10.1109/MCSE.2007.53 (publisher link)
