Neu in 
Jupyter Notebook mit Stata
Jupyter Notebook ist eine leistungsstarke und einfach zu bedienende Webanwendung, die es Ihnen ermöglicht, ausführbaren Code, Visualisierungen, mathematische Gleichungen und Formeln, erzählenden Text und andere reichhaltige Medien in einem einzigen Dokument (einem „Notebook“) für interaktive Berechnungen und Entwicklungen zu kombinieren. Jupyter-Notebooks werden von Forschern und Wissenschaftlern häufig verwendet, um ihre Ideen und Ergebnisse zur Zusammenarbeit und Innovation auszutauschen.
Jetzt können Sie Stata und Mata aus Jupyter-Notizbüchern mit dem IPython-Kernel (interaktives Python) aufrufen, d.h. Sie können die Fähigkeiten von Python und Stata in einer einzigen Umgebung kombinieren, um Ihre Arbeit leicht reproduzierbar zu machen und mit anderen zu teilen.
Lassen Sie uns sehen, wie es funktioniert
In Jupyter Notebook können Sie zwei vom Python-Paket pystata bereitgestellte Werkzeuge verwenden, um mit Stata zu interagieren:
- Drei IPython (interaktives Python) magische Befehle: stata, mata und pystata
- Eine Reihe von API-Funktionen
Bevor wir Ihnen zeigen, wie Sie diese Werkzeuge verwenden können, konfigurieren wir das pystata-Paket. Angenommen, Sie haben Stata in C:\Programme\Stata17\ installiert und verwenden die Stata/MP-Edition. Stata kann wie folgt initialisiert werden:
In [1]:
In [1]:
import stata_setup
stata_setup.config(„C:/Program Files/Stata17“, „mp“)
Höhepunkte
- Aufrufen von Stata aus Python
- Stata mit den magischen Befehlen stata, mata und pystata aufrufen
- Aufrufen von Stata mit einer Reihe von API-Funktionen
- Verwenden Sie die magischen Befehle und API-Funktionen zusammen mit dem Modul Stata Function Interface (sfi)
- Verwenden Sie Python und Stata zusammen
- Zugriff auf Stata und Mata aus Jupyter Notebook, Jupyter Lab und anderen Umgebungen, die den IPython-Kernel unterstützen
- Stata-Daten und -Ergebnisse nach Python übertragen und umgekehrt
- Kombinieren Sie die Fähigkeiten von Stata und Python in einer einzigen Umgebung
___ ____ ____ ____ ____ ©
/__ / ____/ / ____/ 17.0
___/ / /___/ / /___/ MP—Parallel Edition
Statistics and Data Science Copyright 1985-2021 StataCorp LLC
StataCorp
4905 Lakeway Drive
College Station, Texas 77845 USA
800-STATA-PC https://www.stata.com
979-696-4600 stata@stata.com
Stata license: 10-user 4-core network perpetual
Serial number: 1
Licensed to: Stata Developer
StataCorp LLC
Notes:
1. Unicode is supported; see help unicode_advice.
2. More than 2 billion observations are allowed; see help obs_advice.
3. Maximum number of variables is set to 5,000; see help set_maxvar.
.
Wenn Sie eine ähnliche Ausgabe wie die oben gezeigte für Ihre Stata-Edition erhalten, bedeutet dies, dass alles richtig konfiguriert ist; siehe Konfiguration für weitere Möglichkeiten zur Konfiguration von pystata.
Stata mit magic-Befehlen aufrufen
Die stata magic wird verwendet, um Stata-Befehle in einer IPython-Umgebung auszuführen. In einer Notebook-Zelle setzen wir Stata-Befehle unter die %%stata-Zellenmagie, um die Zelle anzuweisen, Stata aufzurufen. Die folgenden Befehle laden den Auto-Datensatz und fassen die Variable mpg zusammen. Die Stata-Ausgabe wird unterhalb der Zelle angezeigt.
In [2]:
%%stata
sysuse auto, clear
summarize mpg
. sysuse auto, clear
(1978 automobile data)
. summarize mpg
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
mpg | 74 21.2973 5.785503 12 41
.
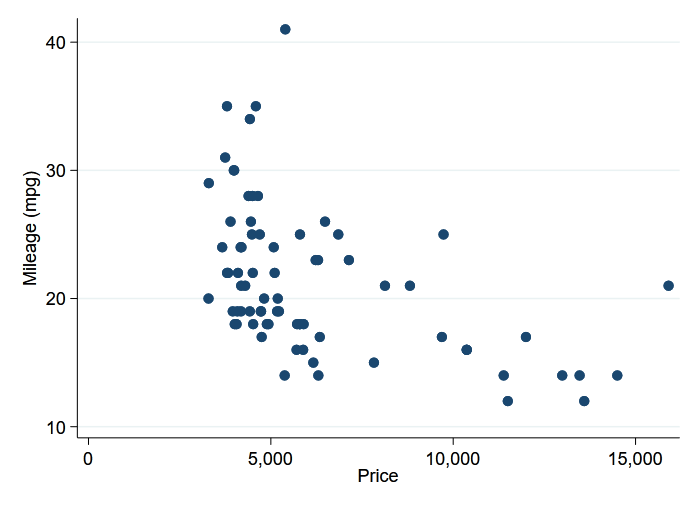
Die Graphen von Stata können auch in der IPython-Umgebung angezeigt werden. Hier erstellen wir ein Streudiagramm der Auto-Kilometerleistung gegen den Preis, indem wir die %stata-Linienmagie verwenden.
In [3]:
%stata scatter mpg price
Als Nächstes laden wir Python-Daten in Stata, führen Analysen in Stata durch und übergeben dann die von Stata zurückgegebenen Ergebnisse an Python zur weiteren Analyse, wobei wir den Second National Health and Nutrition Examination Survey (NHANES II; McDowell et al. 1981) verwenden.
NHANES II, ein Datensatz zum Gesundheits- und Ernährungszustand von Erwachsenen und Kindern in den USA, enthält 10.351 Beobachtungen und 58 Variablen und ist in einer CSV-Datei namens nhanes2.csv gespeichert. Unter diesen Variablen befindet sich eine Indikatorvariable für Bluthochdruck (highbp) und die kontinuierlichen Variablen Alter und Gewicht.
Wir verwenden die Pandas-Methode read_csv(), um die Daten aus der .csv-Datei in einen Pandas-Datenframe namens nhanes2 zu lesen.
In [4]:
import pandas as pd
import io
import requests
data = requests.get(https://www.stata.com/python/pystata/misc/nhanes2.csv“).content
nhanes2 = pd.read_csv(io.StringIO(data.decode(„utf-8“)))
nhanes2
Out [4]:
Wir laden den Datenrahmen in Stata, indem wir das Argument -d des %%stata-Zaubers angeben, und passen dann in Stata ein logistisches Regressionsmodell an, das Alter, Gewicht und deren Interaktion als Prädiktoren für die Wahrscheinlichkeit von Bluthochdruck verwendet. Wir schieben auch die von ereturn list angezeigten Schätzergebnisse von Stata, einschließlich des Koeffizientenvektors e(b) und der Varianz-Kovarianz-Matrix e(V), in ein Python-Wörterbuch namens myeret, indem wir das Argument -eret angeben.
In [5]:
%%stata -d nhanes2 -eret myeret
logistic highbp c.age##c.weight
ereturn list
. logistic highbp c.age##c.weight
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
. ereturn list
scalars:
e(rank) = 4
e(N) = 10351
e(ic) = 4
e(k) = 4
e(k_eq) = 1
e(k_dv) = 1
e(converged) = 1
e(rc) = 0
e(ll) = -5860.151218806021
e(k_eq_model) = 1
e(ll_0) = -7050.765484416371
e(df_m) = 3
e(chi2) = 2381.2285312207
e(p) = 0
e(N_cdf) = 0
e(N_cds) = 0
e(r2_p) = .1688631210670459
macros:
e(cmdline) : "logistic highbp c.age##c.weight"
e(cmd) : "logistic"
e(predict) : "logistic_p"
e(estat_cmd) : "logit_estat"
e(marginsok) : "default Pr"
e(marginsnotok) : "stdp DBeta DEviance DX2 DDeviance Hat Number Resi.."
e(title) : "Logistic regression"
e(chi2type) : "LR"
e(opt) : "moptimize"
e(vce) : "oim"
e(user) : "mopt__logit_d2()"
e(ml_method) : "d2"
e(technique) : "nr"
e(which) : "max"
e(depvar) : "highbp"
e(properties) : "b V"
matrices:
e(b) : 1 x 4
e(V) : 4 x 4
e(mns) : 1 x 4
e(rules) : 1 x 4
e(ilog) : 1 x 20
e(gradient) : 1 x 4
functions:
e(sample)
.
Wir können auf e(b) und e(V) zugreifen, indem wir myeret[‚e(b)‘] bzw. myeret[‚e(V)‘] in Python eingeben. Sie werden in NumPy-Arrays gespeichert.
In [6]:
myeret [‚e(b)‘], myeret[‚e(V)‘]
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Wir verwenden margins und marginsplot, um Vorhersagen über dem Alter grafisch darzustellen, was die Beziehung zwischen Alter und der Wahrscheinlichkeit von Bluthochdruck deutlicher macht.
In [7]:
%%stata
quietly margins, at(age=(20(10)80))
marginsplot
. quietly margins, at(age=(20(10)80)) . marginsplot Variables that uniquely identify margins: age .

Wir verwenden Spannen, um die vorhergesagte Wahrscheinlichkeit von Bluthochdruck für alle Kombinationen von Alter und Gewicht für Werte des Alters zwischen 20 und 80 Jahren in 5er-Schritten und für Werte des Gewichts zwischen 40 und 180 Kilogramm in 5er-Schritten zu schätzen. Die Option saving(predictions, replace) speichert die Vorhersagen in einem Dataset namens predictions.dta. Unser Ziel ist es, mit Python eine dreidimensionale Oberflächendarstellung dieser Vorhersagen zu erstellen.
Der Datensatz predictions.dta enthält die Variablen _at1 und _at2, die den Werten für Alter und Gewicht entsprechen, die wir in der Option at() angegeben haben. Der Datensatz enthält auch die Variable _margin, die die marginale Vorhersage der Wahrscheinlichkeit von Bluthochdruck darstellt. Wir benennen diese Variablen jeweils in Alter, Gewicht und pr_highbp um.
Schließlich speichern wir den Datensatz in Stata als Pandas-Datenframe mit dem Namen preddata in Python, indem wir das Argument -doutd angeben.
In [8]:
%%stata -doutd preddata
quietly margins, at(age=(20(5)80) weight=(40(5)180))
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
Wir listen die ersten fünf Beobachtungen der Spalten Alter, Gewicht, pr_highbp innerhalb des Datenrahmens auf.
In [9]:
preddata[[‚age‘, ‚weight‘, ‚pr_highbp‘]].head()
Out [9]:
Als nächstes verwenden wir Python, um ein dreidimensionales Oberflächendiagramm zu erstellen. Zunächst stellen wir die Größe des Diagramms mit der Methode figure() im pyplot-Modul des Matplotlib-Pakets auf 10 x 8 Zoll ein. Wir verwenden die axes()-Methode, um einen dreidimensionalen Achsensatz mit dem Namen ax zu definieren und zeichnen den Oberflächenplot mit der plot_trisurf()-Methode. Als nächstes setzen wir die Ticks und Beschriftungen für die x-, y- und z-Achse. Zuletzt passen wir die Elevation und den Azimut des.
In [11]:
import matplotlib.pyplot as plt
import numpy as np
# define the axes
fig = plt.figure(1, figsize=(10, 8))
ax = plt.axes(projection=‚3d‘)
# plot
ax.plot_trisurf(preddata[‚age‘], preddata[‚weight‘], preddata[‚pr_highbp‘],cmap=plt.cm.Spectral_r)
# set ticks and labels for x, y, and z axes
ax.set_xticks(np.arange(20, 90, step=10))
ax.set_yticks(np.arange(40, 200, step=40))
ax.set_zticks(np.arange( 0, 1.2, step=0.2))
ax.set_xlabel(Age (years)“)
ax.set_ylabel(Weight (kg)“)
ax.set_zlabel(Probability of Hypertension“)
# adjust the view angle
ax.view_init(elev=30, azim=240)
# show the plot
plt.show()
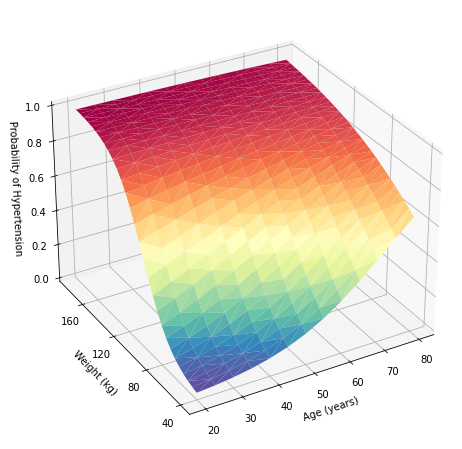
Mit Stata über API-Funktionen interagieren
Wir können auch mit Stata interagieren, indem wir eine Reihe von Funktionen verwenden, die in den Modulen config und stata aus dem Python-Paket pystata definiert sind. Wir werden demonstrieren, wie man diese API-Funktionen zur Interaktion mit Stata als Alternative zum Befehl %%stata magic verwendet.
Wir importieren das stata-Modul aus pystata. Dann rufen wir die Methode pdataframe_to_data() auf, um den Pandas-Datenrahmen nhanes2 in Stata zu laden und rufen die Methode run() auf, um das logistische Regressionsmodell anzupassen.
In [12]:
from pystata import
stata
stata.pdataframe_to_data(nhanes2, force=True)
stata.run(‚logistic highbp c.age##c.weight‘)
Logistic regression Number of obs = 10,351
LR chi2(3) = 2381.23
Prob > chi2 = 0.0000
Log likelihood = -5860.1512 Pseudo R2 = 0.1689
------------------------------------------------------------------------------
highbp | Odds ratio Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
age | 1.108531 .0080697 14.15 0.000 1.092827 1.12446
weight | 1.081505 .005516 15.36 0.000 1.070748 1.092371
|
c.age#|
c.weight | .9992788 .0000977 -7.38 0.000 .9990873 .9994703
|
_cons | .0002025 .0000787 -21.89 0.000 .0000946 .0004335
------------------------------------------------------------------------------
Note: _cons estimates baseline odds.
Dann verwenden wir die Methode get_ereturn(), um die vom logistischen Befehl zurückgegebenen e()-Ergebnisse in Python als Wörterbuch namens myeret2 zu speichern und darin e(b) und e(V) anzuzeigen.
In [13]:
myeret2 = stata.get_ereturn()
myeret2[‚e(b)‘], myeret2[‚e(V)‘]
Out [13]:
(array([[ 1.03035513e-01, 7.83537342e-02, -7.21492384e-04,
-8.50485078e+00]]),
array([[ 5.29930771e-05, 3.50509317e-05, -6.97861002e-07,
-2.69423163e-03],
[ 3.50509317e-05, 2.60132664e-05, -4.74084051e-07,
-1.94299575e-03],
[-6.97861002e-07, -4.74084051e-07, 9.55811835e-09,
3.50377699e-05],
[-2.69423163e-03, -1.94299575e-03, 3.50377699e-05,
1.50887842e-01]]))
Als nächstes rufen wir die run()-Methode auf, um die vorhergesagte Wahrscheinlichkeit von Bluthochdruck für alle Kombinationen von Alter und Gewicht zu schätzen, speichern die Vorhersageergebnisse in einem Datensatz mit dem Namen predictions.data und laden den Datensatz in Stata und benennen die Variablen um.
In [14]:
stata.run(“‘
quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
saving(predictions, replace)
use predictions, clear
list _at1 _at2 _margin in 1/5
rename _at1 age
rename _at2 weight
rename _margin pr_highbp
“‘)
.
. quietly margins, at(age=(20(5)80) weight=(40(5)180)) ///
> saving(predictions, replace)
.
. use predictions, clear
(Created by command margins; also see char list)
. list _at1 _at2 _margin in 1/5
+------------------------+
| _at1 _at2 _margin |
|------------------------|
1. | 20 40 .0200911 |
2. | 20 45 .0274497 |
3. | 20 50 .0374008 |
4. | 20 55 .0507709 |
5. | 20 60 .0685801 |
+------------------------+
. rename _at1 age
. rename _at2 weight
. rename _margin pr_highbp
.
Wir rufen die Funktion pdataframe_from_data() im Stata-Modul auf, um das Alter, das Gewicht und pr_highbp im aktuellen Datensatz in einem Pandas-Datenframe namens preddata2 zu speichern.
In [15]:
preddata2 = stata.pdataframe_from_data(var=„age weight pr_highbp“)
preddata2.head()
Out [15]:
Sobald wir diesen Datenrahmen haben, können wir die gleiche dreidimensionale Oberflächendarstellung wie oben erstellen.
Beachten Sie, dass Sie auch das Modul Stata Function Interface (sfi) verwenden können, um auf die Kernfunktionen von Stata zuzugreifen. Die Kombination dieser Werkzeuge macht es viel einfacher, mit Stata von Jupyter Notebook aus zu interagieren; siehe Beispiel 5: Stata mit API-Funktionen aufrufen für ein Beispiel.
Referenzen
Jäger, J. D. 2007. Matplotlib: A 2D Graphics Environment. Computing in Science & Engineering 9: 90-95.
McDowell, A., A. Engel, J. T. Massey, und K. Maurer. 1981. Plan und Durchführung des Second National Health and Nutrition Examination Survey, 1976-1980. Vital and Health Statistics 1(15): 1-144.
Mckinney, W. 2010. Data Structures for Statistical Computing in Python. Proceedings of the 9th Python in Science Conference, 56-61. (publisher link).
Oliphant, T. E. 2006. A Guide to NumPy, 2nd ed. Austin, TX: Continuum Press.
Péz, F., and B. E. Granger. 2007. IPython: A System for Interactive Scientific Computing, Computing in Science and Engineering 9: 21–29. DOI:10.1109/MCSE.2007.53 (publisher link)
