New In 
Moyenne des modèles bayésiens (BMA) pour la régression linéaire
Pourquoi choisir un seul modèle quand vous pouvez emprunter des informations à plusieurs ? La nouvelle suite bma effectue une moyenne de modèle bayésienne pour tenir compte de l’incertitude du modèle dans votre analyse. Vous ne savez pas quels prédicteurs inclure dans votre modèle de régression linéaire ? Utilisez bmaregress pour déterminer quels prédicteurs sont importants. Effectuer le choix du modèle, l’inférence et la prédiction. Utilisez de nombreuses commandes de post-estimation pour explorer les modèles influents, la complexité des modèles, l’ajustement des modèles et la performance prédictive, l’analyse de sensibilité aux hypothèses sur l’importance des modèles et des prédicteurs, et bien plus encore.
Points forts
-
Choix du modèle, inférence et prédiction
-
Dénombrement des modèles et échantillonnage MC3
-
Prédicteurs toujours inclus et groupés
-
A priori du modèle : uniforme, binomial, bêta-binomial
-
De nombreux g-priors, y compris hyper-g et robustes
-
Variables factorielles et opérateurs de séries temporelles
-
Hérédité forte, faible ou nulle pour les interactions
-
Convergence BMA MCMC
-
Modèle postérieur et probabilités d’inclusion
-
Distributions a priori et a posteriori de la taille des modèles
-
Distributions postérieures des paramètres du modèle
-
Mesures de jointure pour les paires de prédicteurs
-
Cartes d’inclusion de variables
-
Score prédictif logarithmique pour l’adéquation du modèle et la performance de la prédiction
-
Analyse de sensibilité
-
Prédiction
-
Prise en charge des fonctions standard de post-estimation bayésienne
-
Voir plus d’informations Moyenne des modèles bayésiens caractéristiques
Introduction
Traditionnellement, nous sélectionnons un modèle et effectuons une inférence et une prédiction conditionnelles à ce modèle. Nos résultats ne tiennent généralement pas compte de l’incertitude liée à la sélection d’un modèle et peuvent donc être trop optimistes. Ils peuvent même être incorrects si le modèle sélectionné est sensiblement différent du véritable modèle générateur de données (DGM). Dans certaines applications, nous pouvons disposer de preuves théoriques ou empiriques solides concernant le DGM. Dans d’autres applications, généralement de nature complexe et instable, comme celles de l’économie, de la psychologie et de l’épidémiologie, le choix d’un modèle fiable peut s’avérer difficile. Au lieu de s’appuyer sur un seul modèle, le calcul de la moyenne des modèles établit une moyenne des résultats sur plusieurs modèles plausibles basés sur les données observées. Dans la BMA, la « plausibilité » du modèle est décrite par la probabilité postérieure du modèle (PMP), qui est déterminée à l’aide des principes bayésiens fondamentaux – le théorème de Bayes – et appliquée universellement à toutes les analyses de données. La BMA peut être utilisée pour tenir compte de l’incertitude du modèle lors de l’estimation des paramètres du modèle et de la prédiction de nouvelles observations, afin d’éviter des conclusions trop optimistes. Il est particulièrement utile dans les applications comportant plusieurs modèles plausibles, lorsqu’il n’y a pas de raison définitive de choisir un modèle particulier plutôt qu’un autre. Mais même si le choix d’un modèle unique est l’objectif final, la BMA peut s’avérer utile. Il fournit une méthode fondée sur des principes pour identifier les modèles et les prédicteurs importants au sein des classes de modèles considérées. Son cadre vous permet de connaître les interrelations entre différents prédicteurs en termes de tendance à apparaître dans un modèle ensemble, séparément ou indépendamment. Il peut être utilisé pour évaluer la sensibilité des résultats finaux à diverses hypothèses sur l’importance des différents modèles et prédicteurs. Il fournit des prédictions optimales au sens du log-score.
La suite bma
Dans le cadre d’une régression, l’incertitude du modèle correspond à l’incertitude quant aux prédicteurs à inclure dans un modèle. Nous pouvons utiliser bmaregress pour prendre en compte la sélection des prédicteurs dans une régression linéaire. Il explore l’espace des modèles soit de manière exhaustive avec l’option d’énumération, lorsque cela est possible, soit en utilisant l’algorithme de composition de modèles (MC3) de la chaîne de Markov Monte Carlo (MCMC) avec l’option d’échantillonnage. Il fournit divers résumés des modèles visités et des prédicteurs inclus, ainsi que des distributions a posteriori des paramètres du modèle. Il vous permet de spécifier des groupes de prédicteurs à inclure ou à exclure ensemble d’un modèle et ceux qui sont inclus dans tous les modèles. Il fournit diverses distributions a priori pour les modèles dans l’option mprior() et pour le paramètre g, qui contrôle le rétrécissement des coefficients de régression vers zéro, dans l’option gprior(). Il prend également en charge les variables factorielles et les opérateurs de séries temporelles et propose plusieurs façons de gérer les interactions pendant l’estimation en utilisant l’option heredity().
De nombreuses fonctions de post-estimation sont prises en charge, y compris certaines des fonctions de post-estimation bayésienne standard.
| Commandement | Description |
|---|---|
|
Échantillons postérieurs de coefficients de régression |
|
|
les diagrammes modèle-probabilité |
|
|
les diagrammes de distribution de la taille des modèles |
|
|
cartes à inclusion variable |
|
|
coefficient de densité postérieure |
|
|
modèle postérieur et résumés d’inclusion de variables |
|
|
résumé de la taille du modèle |
|
|
les probabilités d’inclusion a posteriori (PIP) pour les prédicteurs |
|
|
mesures de jointure pour les prédicteurs |
|
|
score prédictif logarithmique (LPS) |
|
|
Prévisions de la BMA |
|
|
Résumés graphiques bayésiens et diagnostics de convergence |
|
|
Statistiques sommaires bayésiennes pour les paramètres des modèles et leurs fonctions |
|
|
Tailles d’échantillon efficaces selon la méthode bayésienne et statistiques connexes |
|
|
Valeurs p prédictives bayésiennes |
|
|
Prédictions bayésiennes |
Voyons comment cela fonctionne
-> Énumération des modèles -> Intervalles crédibles -> Modèles influents -> Facteurs prédictifs importants ->Répartition de la taille des modèles -> Distributions postérieures des coefficients -> Prévision de la BMA -> Aprioris informatifs sur les modèles -> Performance prédictive grâce au LPS -> Nettoyage
Ci-dessous, nous présentons quelques caractéristiques de bma à l’aide d’un jeu de données fictif. Cet ensemble de données contient n=200
�=200 observations, p=10 �=10 prédicteurs orthogonaux et le résultat y généré comme suit
y=0,5+1,2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
où ϵ∼N(0,1)
�∼�(0,1) est un terme d’erreur normal standard.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Énumération des modèles
Nous utilisons bmaregress pour ajuster une régression linéaire BMA de y sur x1 à x10.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272
| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
Avec 10 prédicteurs et le g-prior fixe par défaut (benchmark), bmaregress utilise l’énumération de modèles et explore tous les 210=1 024
210=1 024 modèles possibles. L’a priori du modèle par défaut est bêta-binomial avec des paramètres de forme de 1, qui est uniforme sur la taille du modèle. A priori, notre modèle BMA supposait une faible contraction des coefficients de régression vers zéro car g/(1+g)=0,9950 �/(1+�)=0,9950 est proche de 1.
bmaregress a identifié x2 et x10 comme des variables prédictives très importantes – leurs probabilités d’inclusion a posteriori (PIP) sont pratiquement égales à 1. Les estimations moyennes a posteriori de leurs coefficients de régression sont respectivement de 1,2 (arrondi) et de 5,1 et sont très proches des valeurs réelles de 1,2 et de 5. Tous les autres prédicteurs ont des PIP beaucoup plus faibles et des estimations de coefficient proches de zéro. Les résultats de notre BMA sont cohérents avec le véritable DGM.
Stockons nos résultats d’estimation actuels pour une utilisation ultérieure. Comme pour les autres commandes bayésiennes, nous devons d’abord enregistrer les résultats de la simulation avant de pouvoir utiliser estimates store pour stocker les résultats de l’estimation.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Intervalles crédibles
Par défaut, bmaregress n’indique pas les intervalles crédibles (CrI), car cela nécessite une simulation potentiellement longue de l’échantillon postérieur des paramètres du modèle. Mais nous pouvons les calculer après l’estimation.
Nous utilisons d’abord bmacoefsample pour générer un échantillon MCMC à partir de la distribution postérieure des paramètres du modèle, qui incluent les coefficients de régression. Nous utilisons ensuite la commande bayesstats summary existante pour calculer les résumés a posteriori de l’échantillon MCMC généré.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
L’indice de confiance à 95 % pour le coefficient x2 est de [1,05, 1,34], et celui pour x10 est de [4,9, 5,26], ce qui est cohérent avec notre DGM.
Modèles influents
La moyenne des estimations des coefficients BMA est calculée sur 1 024 modèles. Il est important de déterminer quels sont les modèles influents. Nous pouvons utiliser les modèles bmastats pour explorer les PMP.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Sans surprise, le modèle qui contient à la fois x2 et x10 a le PMP le plus élevé, soit environ 63 %. En fait, les deux premiers modèles correspondent à un PMP cumulé d’environ 77 % :
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2
| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
Nous pouvons utiliser bmagraph pmp pour tracer le PMP cumulé.
. bmagraph pmp, cumulative

La commande trace les 100 premiers modèles par défaut, mais vous pouvez spécifier l’option top() si vous souhaitez voir plus de modèles.
Prédicteurs importants
Nous pouvons explorer visuellement l’importance des prédicteurs en utilisant bmagraph varmap pour produire une carte d’inclusion de variables.
. bmagraph varmap Computing model probabilities ...

x2 et x10 sont inclus dans les 100 premiers modèles, classés par PMP. Leurs coefficients sont positifs dans tous les modèles.
Distribution de la taille du modèle
Nous pouvons explorer la complexité de notre modèle BMA en utilisant bmastats msize et bmagraph msize pour explorer les distributions a priori et a posteriori de la taille du modèle.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
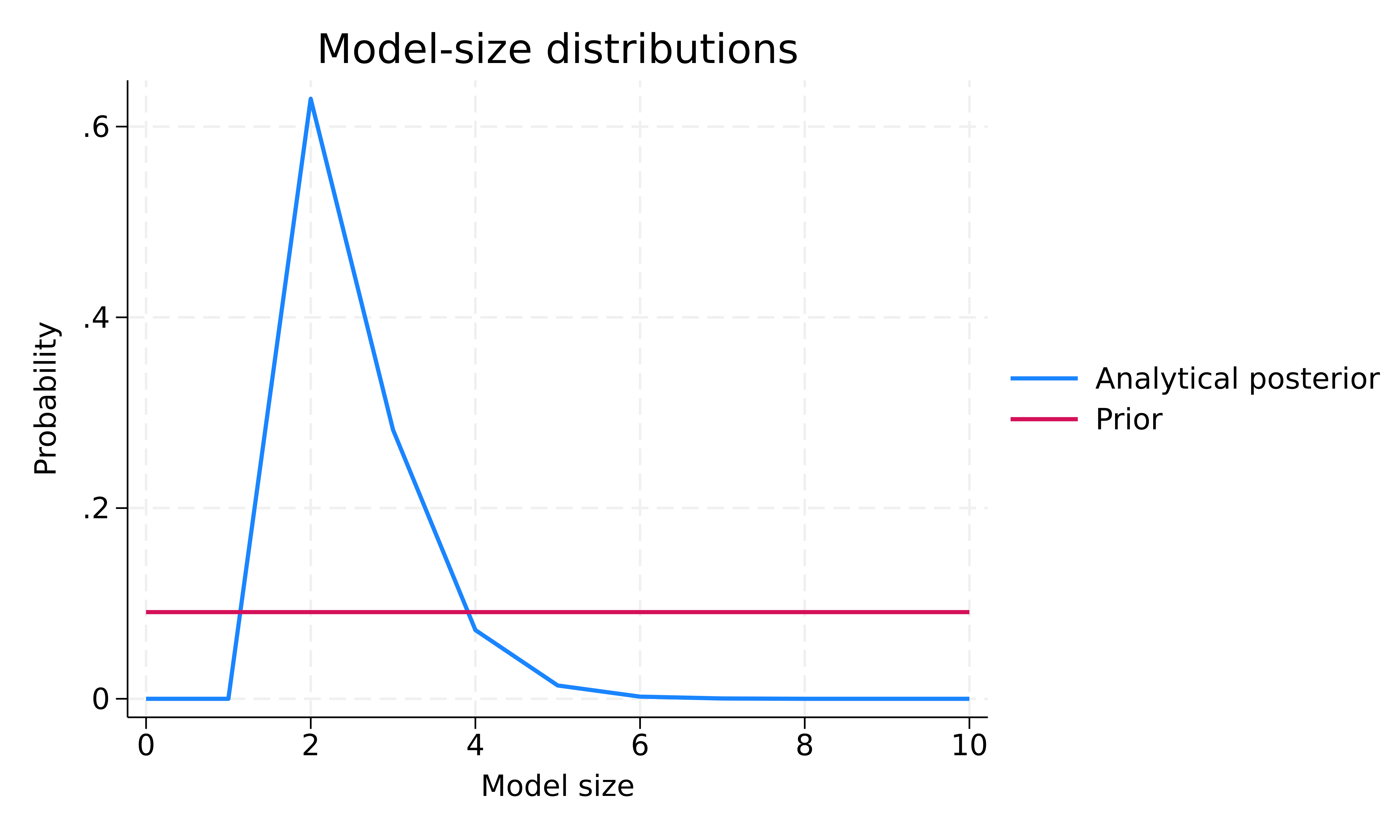
La distribution a priori de la taille du modèle est uniforme sur la taille du modèle. La distribution a posteriori de la taille du modèle est asymétrique vers la gauche avec un mode d’environ 2. La taille moyenne du modèle a priori est de 5 et celle a posteriori est de 2,48. Ainsi, sur la base des données observées, BMA tend à favoriser des modèles plus petits avec environ deux prédicteurs, en moyenne, par rapport à notre hypothèse a priori.
Distributions postérieures des coefficients
Nous pouvons utiliser bmagraph coefdensity pour tracer les distributions postérieures des coefficients de régression.
. bmagraph coefdensity {x2} {x3}, combine
Ces distributions sont des mélanges d’une masse ponctuelle à zéro correspondant à la probabilité de non-inclusion du prédicteur et d’une densité continue conditionnelle à l’inclusion. Pour le coefficient x2, la probabilité de non-inclusion est négligeable, de sorte que sa distribution postérieure est essentiellement une densité continue, assez symétrique, centrée sur 1,2. Pour le coefficient x3, en plus de la densité continue conditionnelle, il y a une ligne verticale rouge à zéro correspondant à la probabilité postérieure de non-inclusion d’environ 1-.2 = 0.8.
Prédiction BMA
bmapredict produit diverses prédictions BMA. Par exemple, calculons les moyennes prédictives postérieures.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Nous pouvons également calculer des indices de corrélation prédictifs pour estimer l’incertitude de nos prédictions (ce qui n’est pas possible avec de nombreuses méthodes traditionnelles de sélection de modèles). (Notez que ces indices de corrélation prédictifs intègrent également l’incertitude du modèle. Pour calculer les indices de corrélation prédictifs, nous devons d’abord sauvegarder l’échantillon de paramètres de modèle MCMC a posteriori.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Nous résumons les résultats prévus :
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Les moyennes rapportées sur les observations pour les moyennes prédictives et les limites inférieures et supérieures à 95 % du CrI prédictif semblent raisonnables par rapport au résultat observé y.
Informations préalables sur les modèles
L’un des points forts de BMA est la possibilité d’intégrer des informations préalables sur les modèles et les prédicteurs. Cela nous permet d’étudier la sensibilité des résultats à diverses hypothèses sur l’importance des modèles et des prédicteurs. Supposons que nous disposions d’informations fiables selon lesquelles tous les prédicteurs, à l’exception de x2 et x10, sont moins susceptibles d’être liés au résultat. Nous pouvons spécifier, par exemple, un modèle binomial a priori avec de faibles probabilités d’inclusion a priori pour ces prédicteurs.
Pour comparer ultérieurement les performances hors échantillon des modèles BMA, nous divisons aléatoirement notre échantillon en deux parties et ajustons le modèle BMA à l’aide du premier sous-échantillon. Nous sauvegardons également les résultats de ce modèle BMA plus informatif.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
L’effet de cette priorité de modèle est que le PIP de tous les prédicteurs sans importance est maintenant inférieur à 2 %.
Notez que lorsque nous sélectionnons un modèle, nous ajustons essentiellement un modèle BMA avec un a priori très fort selon lequel tous les prédicteurs sélectionnés doivent être inclus avec une probabilité de 1. Par exemple, nous pouvons forcer bmaregress à inclure toutes les variables dans le modèle :
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Performance prédictive à l’aide de LPS
Pour comparer les modèles BMA envisagés, nous réajustons notre modèle BMA par défaut en utilisant le premier sous-échantillon et nous stockons les résultats de l’estimation.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Nous pouvons comparer la performance prédictive hors échantillon de nos modèles BMA en utilisant bmastats lps pour calculer le logarithme du score prédictif (LPS) pour les observations hors échantillon.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Le modèle bmareg_inf, plus informatif, a un LPS moyen légèrement inférieur, mais les résumés LPS de tous les modèles sont très similaires. Voir [BMA] bmastats lps pour savoir comment comparer les performances des modèles BMA en utilisant la validation croisée.
Nettoyage
Nous avons généré plusieurs ensembles de données au cours de notre analyse. Nous n’en avons plus besoin et nous les effaçons à la fin. Mais vous pouvez décider de les conserver, surtout s’ils correspondent à une analyse finale qui pourrait prendre beaucoup de temps.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
