Ново в 
Байесови линейни и нелинейни DSGE модели
Префиксът bayes вече поддържа командите dsge и dsgenl за настройка на линейни и нелинейни динамични стохастични модели на общото равновесие (DSGE) по метода на Бейс.
DSGE моделите са популярни в макроикономиката и финансите за моделиране на множество времеви редове. Моделите съдържат системи от линейни или нелинейни уравнения, които описват различни икономически процеси. Параметрите на DSGE моделите обикновено имат пряко тълкуване в контекста на икономическата теория и често имат установени диапазони на правдоподобни стойности. Тези диапазони (или ограничения) трябва да бъдат включени в оценката, за да се получат стабилни резултати.
Байесовата оценка предоставя естествен начин за включване на такива ограничения чрез определяне на различни предварителни разпределения за параметрите на модела, които удовлетворяват ограниченията.
Нека видим как работи
Линеен DSGE модел
DSGE моделът се състои от система уравнения, които свързват икономическите променливи, като инфлацията, лихвения процент и производствената разлика, помежду им и с екзогенните променливи на състоянието, които управляват системата.
Акценти
- Байесови динамични стохастични модели на общото равновесие
- Линейни и нелинейни модели
- Предпоставки по подразбиране и по избор
- Гъвкаво управление на MCMC извадката
- Байесова обобщена статистика
- Диагностика MCMC
- Множество вериги
- Функции на импулсен отговор
- Графики и таблици на IRF
- Запазване и сравняване на модели
- Пълна поддръжка на Байесовите функции за последваща оценка
Уравненията могат да бъдат динамични в два смисъла: изоставанията отразяват поведението, насочено назад, докато очакваните бъдещи стойности отразяват поведението, насочено напред. DSGE моделите могат да се използват за анализ на политики, като например ефекта от парични шокове, фискални шокове и др.
Байесовата оценка се състои от две стъпки: определяне на DSGE модела и определяне на прийорите за параметрите на DSGE модела.
Един малък новокейнсиански модел има уравнение за инвестиране и спестяване (IS), което свързва разликата в производството с лихвения процент, крива на Филипс, която свързва инфлацията с разликата в производството, и правило на Тейлър, което свързва лихвения процент с инфлацията. В синтаксиса на Stata моделът изглежда по следния начин:
( x = F.x - (r - F.p - z) , unobserved ) ///
( p = {beta}*F.p + {kappa}*x ) ///
( r = 1/{delta}*p + m ) ///
( F.z = {rhoz}*z, state ) ///
( F.m = {rhom}*m, state )
Първото уравнение е кривата на IS, второто е кривата на Филипс, а третото е правилото на Тейлър. Четвъртото уравнение е IS шок, а петото – паричен шок по правилото на Тейлър.
Опцията unobserved в кривата на IS показва, че разглеждаме разликата в производството като ненаблюдавана. Приспособихме модела към данните за инфлацията и лихвения процент.
Добавяме предварителна спецификация за всеки параметър. Много параметри на DSGE имат интерпретации, които естествено ограничават обхвата на допустимите стойности. Параметърът {beta} в кривата на Филипс е дисконтовият процент и трябва да лежи между 0 и 1. Параметърът {kappa} е параметър за коригиране на цените, за който често се смята, че е малък, но положителен. Параметърът {delta} е обратният на правилото на Тейлър коефициент на корекция на инфлацията, така че той трябва да лежи между 0 и 1. В допълнение към тези ограничения на обхвата може да има и предварителни оценки за вероятното местоположение на стойността на параметъра. Сконтовият процент вероятно е около 0,95, параметърът за корекция на инфлацията – около 0,2, а обратният коефициент за корекция на инфлацията – около 0,66 (за коефициент по правилото на Тейлър 1,5). Приоритетите ви позволяват да включите тази информация изрично в оценяването.
Разгледайте данните за темпа на инфлация и лихвения процент по федералните фондове от 1955 г. насам.
. webuse usmacro2 (Federal Reserve Economic Data - St. Louis Fed, 2017-01-15) . describe p r
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| p double %10.0g Growth rate of prices (GDPDEF) | ||
| r double %10.0g Federal funds rate (FEDFUNDS) | ||
| Variable | Obs Mean Std. dev. Min Max | |
| p | 2.44 3.236709 2.281433 -.6681431 11.60957 | |
| r | 2.44 5.035328 3.59569 .07 19.1 |
Събирайки както предварителната спецификация, така и спецификацията на модела, нашата команда за оценка е
. bayes, prior({beta}, beta(95,5)) ///
prior({kappa}, beta(30,70)) ///
prior({delta}, beta(60,30)) ///
prior({rhoz}, beta(10,10)) ///
prior({rhom}, beta(10,10)) ///
rseed(17) : ///
dsge ( x = F.x - (r - F.p - z), unobserved) ///
( p = {beta}*F.p + {kappa}*x ) ///
( r = 1/{delta}*p + m ) ///
(F.z = {rhoz}*z, state ) ///
(F.m = {rhom}*m, state )
note: initial parameter vector set to means of priors.
Burn-in ...
Simulation ...
Model summary
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| beta | .9406005 .0243801 .001984 .9428465 .8869374 .9812481 | |
| kappa | .206337 .0327608 .001679 .2046031 .1470858 .273637 | |
| delta | .5832685 .0404188 .004897 .5835278 .497712 .6607058 | |
| rhoz | .9171911 .015764 .000978 .9170596 .8846393 .9467265 | |
| rhom | .561412 .0296339 .001667 .5621747 .5036024 .6184265 | |
| sd(e.z) | .5280986 .057275 .003639 .5255331 .4217194 .6467684 | |
| sd(e.m) | 2.161816 .1585077 .020872 2.141682 1.902066 2.533669 | |
Обобщението на модела показва вероятностния модел и предварителните спецификации. Изискват се приори за всички, освен за стандартните отклонения. В случая на DSGE моделите това има смисъл, тъй като параметрите са свързани с икономическата теория. Например, приорът за дисконтовия фактор {beta} е бета с параметри на формата 95 и 5. На стандартните отклонения на шоковете на променливите на състоянието z и m са зададени обратни гама приори по подразбиране.
Резултатът от оценката показва броя на периодите на изгаряне (2500), размера на MCMC извадката (10 000), размера на извадката от данни (244 периода), периода на извадката (1955q1 до 2015q4), както и степента на приемане и ефективността на процеса на оценка. Коефициентът на приемане се отнася до частта от тегленията на MCMC, които са били приети. Типичните стойности за използвания извадкообразувател на Метрополис-Хастингс са 20-30 %; нашата норма на приемане е 24 %. Ефикасността е свързана с автокорелацията на MCMC тегленията и показва колко бързо пробовземането преминава през пространството на параметрите. Средната ни ефективност е 2,1 %.
Изходът от оценката показва средните стойности на параметрите, стандартните отклонения, медианите и равните доверителни интервали. Постериорната средна стойност на {beta} е 0,94, много близка до нейната предварителна средна стойност от 0,95. Постериорната средна стойност на {kappa} е около 0,21, което е по-ниско от предходната средна стойност от 0,30. Постериорната средна стойност на {delta} е 0,58, което е по-ниско от предходната средна стойност от 0,66. И двата шока са силно устойчиви, като средните апостериорни коефициенти на автокорелация за z и m са съответно 0,92 и 0,56. Апостериорните средни стойности на стандартните отклонения на шоковете са 0,53 за шока от IS z и 2,16 за паричния шок по правилото на Тейлър m.
Всички байесовски функции на Stata за последващи оценки работят след bayes: dsge.
Можем да начертаем апостериорната плътност на параметъра на предварителната корекция {kappa}.
. bayesgraph kdensity {kappa}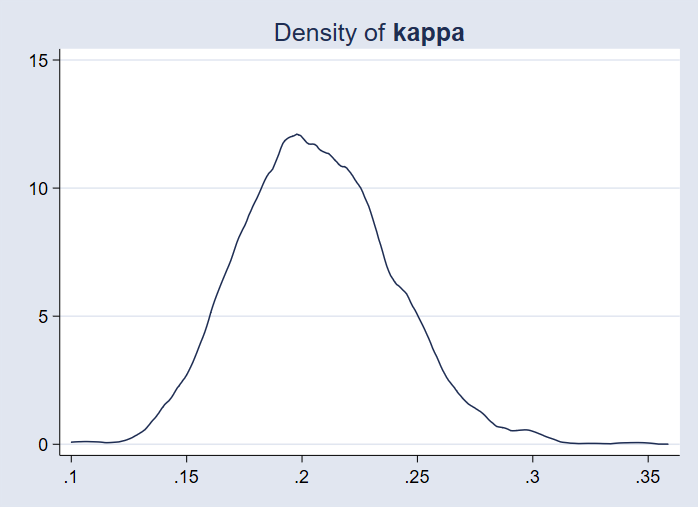
Можем да начертаем пълен набор от диагностики за {kappa}.
. bayesgraph diagnostics {kappa}
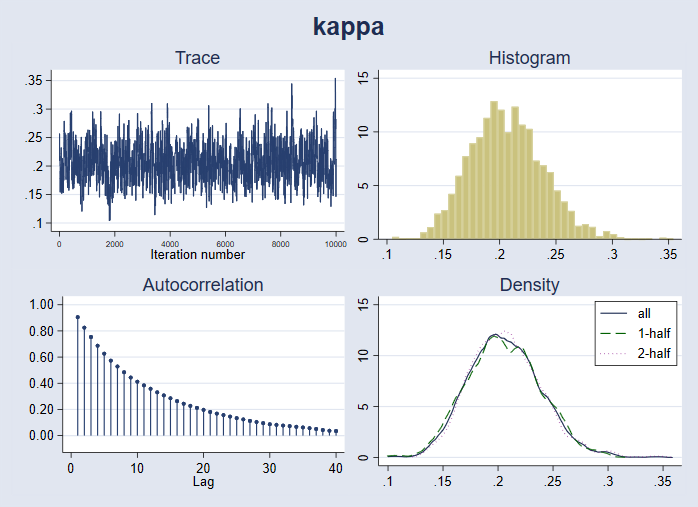
Можем да добавим предварителната плътност към диаграмата на постериорната плътност, за да сравним визуално предварителната и постериорната плътност.
. bayesgraph kdensity kappa, addplot(function Prior = betaden(30,70,x), ///
legend(on label(1 "Posterior")) lcolor(blue))

Можем да разгледаме апостериорните плътности на функциите на параметрите на модела, като например коефициента на правилото на Тейлър 1/{delta}.
. bayesstats summary (1/{delta})
Posterior summary statistics MCMC sample size = 10,000
expr1 : 1/delta
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| expr1 | 1.722922 .1225577 .015302 1.713714 1.513533 2.009195 | |
Постериорната средна стойност за 1/{delta} е 1,7, което е по-високо от предходната средна стойност от 1,5 и показва силна реакция на лихвените проценти на промените в инфлацията.
Можем да изчислим Байесовите функции на импулсен отговор. Първо, записваме резултатите от MCMC в набор от данни, nk_mcmc.dta. Можем да направим това по време на оценяването с опцията saving() или дори след оценяването, като повторим командата bayes с опцията saving().
. bayes, saving(nk_mcmc.dta, replace) note: file nk_mcmc.dta not found; file saved.
След като извадката MCMC е запазена, можем да конструираме функциите импулс-отговор с пакета bayesirf. Този набор от команди разширява irf, за да се приспособи към Байесовата оценка, и е достъпен след bayes: dsge, bayes: dsgenl и bayes: var.
. bayesirf set bayes_irfs.irf, replace (file bayes_irfs.irf created) (file bayes_irfs.irf now active) . bayesirf create nk_model (file bayes_irfs.irf updated) . bayesirf graph irf, impulse(m) response(x p r m)

В горния ляв панел е показана реакцията на променливата на паричното състояние m на шок върху самата нея. В горния десен панел е показана реакцията на инфлацията на шока: тя намалява, след което се връща монотонно към устойчивото състояние. В долния ляв панел е показана реакцията на лихвения процент: той се повишава. И накрая, долният десен панел показва реакцията на производствената разлика: тя пада под 0, което означава рецесия. По този начин рестриктивният паричен шок повишава лихвения процент, намалява инфлацията и предизвиква спад на производството.
Всичко това и още много други неща могат да се направят с командата bayes: dsge.
Нелинеен DSGE модел
Префиксът bayes работи и с командата dsgenl, която оценява параметрите на нелинейни DSGE модели чрез пертурбация от първи ред.
След това оценяваме параметрите на стохастичен модел на растежа. Моделът има уравнения за потреблението, реалния лихвен процент, БВП, капиталовата маса и производителността.
(1/c = {beta}*(1/F.c)*(1+F.r-{delta}) ) ///
(r = {alpha}*y/k ) ///
(y = z*k^({alpha}) ) ///
(f.k = y - c + (1-{delta})*k ) ///
(ln(f.z) = {rho}*ln(z) ) , ///
exostate(z) endostate(k) observed(y) unobserved(c r)
Макроикономистите разпознават тези връзки съответно като уравнение на Ойлер за потреблението, уравнение на търсенето на капитал, производствена функция, уравнение на натрупването на капитал и закон за движението на производителността.
Параметрите имат интерпретация: {beta} е нормата на дисконтиране, която обикновено се смята за около 0,95; {alpha} е делът на капитала в дохода, който обикновено се смята за около една трета; {delta} е нормата на амортизация, която обикновено е 2,5 % на тримесечие; и {rho} е устойчивостта на технологичния шок. Използват се приори, за да се включи тази информация в оценката.
Оценяваме параметрите на този модел, като използваме детерминирана продукция. Наборът от данни m1gdp.dta предоставя логаритъма на продукцията.
. webuse m1gdp, clear
. describe
Contains data from https://www.stata-press.com/data/r17/m1gdp.dta
Observations: 223
Variables: 3 26 Mar 2020 02:49
| Variable Storage Display Value | ||
| name type format label Variable label | ||
| t int %tq Quarterly time variable | ||
| ln_m1 float %9.0g ln(M1) monthly to quarterly by | ||
| averaging: M1 is Fred M1SL, Bil | ||
| of $ seas adj | ||
| ln_gdp float %9.0g ln(gdpc1) FRED GDP in Bil of 1996 | ||
| chained $ seas adj | ||
Командата tsfilter извлича компонента на тенденцията в изхода. Използваме филтър на Ходрик-Прескот и след това увеличаваме резултата с коефициент 100. Получената скала е такава, че стойност 1 означава, че БВП е с 1% над стойността на тренда.
. tsfilter hp y = ln_gdp
. replace y = 100*y
(222 real changes made)
. tsline y, title("HP-detrended output")

Рецесиите се свързват със спад на производството под тенденцията, докато бумът е свързан с нарастване на производството над тенденцията.
Продължаваме с оценката на параметрите.
. bayes, prior({alpha}, beta(30,70)) ///
prior({beta}, beta(95,5)) ///
prior({delta}, beta(25,900)) ///
prior({rho}, beta(10, 10)) ///
rseed(20) dots saving(rbc_mcmc, replace): ///
dsgenl (1/c = {beta}*(1/F.c)*(1+f.r-{delta}) ) ///
(r = {alpha}*y/k ) ///
(y = z*k^({alpha}) ) ///
(f.k = y - c + (1-{delta})*k ) ///
(ln(f.z) = {rho}*ln(z) ) , ///
exostate(z) endostate(k) observed(y) unobserved(c r)
note: initial parameter vector set to means of priors.
Burn-in 2500 aaaaaaaaa1000aaaaaa...2000..... done
Simulation 10000 .........1000.........2000.........3000.........4000.........
5000.........6000.........7000.........8000.........9000.........10000 done
Model summary
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| beta | .9095501 .0392698 .001886 .9133171 .8231531 .9726171 | |
| delta | .0286052 .0054865 .000345 .0284 .0192159 .0404854 | |
| alpha | .2768864 .0451422 .002097 .2738962 .1964999 .3772306 | |
| rho | .7680742 .036755 .001813 .7680699 .6950177 .8412948 | |
| sd(e.z) | .9340691 .0458306 .001943 .9328126 .8502487 1.032548 | |
Предходната средна стойност на дисконтовия процент {beta} е 0,95; нейната последна средна стойност е малко променена и е 0,91. Предварителната средна стойност на нормата на обезценяване {delta} е 0,025; нейната апостериорна средна стойност е малко променена и е 0,0286. Предходната средна стойност на {alpha} е 0,3; нейната апостериорна средна стойност е малко по-ниска – 0,28. В същото време апостериорната средна стойност на {rho} е 0,77, което е много повече от нейната предварителна средна стойност от 0,5. Стандартното отклонение на технологичния шок е около 1.
След това изчисляваме функциите „импулс – отговор“ на технологичния шок.
. bayesirf set bayes_irf2.irf, replace (file bayes_irf2.irf created) (file bayes_irf2.irf now active) . bayesirf create rbc_model, step(16) (file bayes_irf2.irf updated) . bayesirf graph irf, impulse(z) byopts(yrescale)
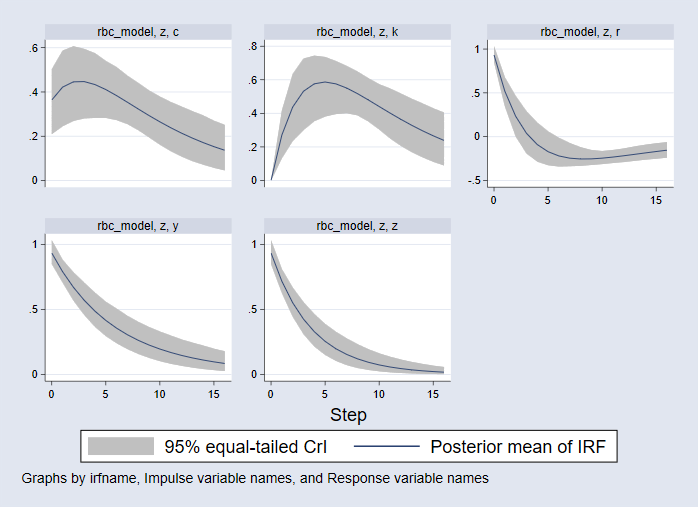
Мерните единици по вертикалната ос са в проценти на отклоненията от стационарното състояние. Мерните единици по хоризонталната ос са в същата времева продължителност като данните, т.е. в тримесечия. Изведени са 16 етапа (4 години) от отговори.
- Отговорът на потреблението е показан в горния ляв панел. Потреблението се повишава в момента на въздействието и след това продължава да нараства по гърбицовиден модел, преди да се върне към устойчивото си състояние.
- Реакцията на капиталовите запаси е показана в горната част на средния панел. Капиталовият запас не се променя в момента на въздействието, но след това се повишава до връх от 0,6% над устойчивото си състояние, след което спада.
- В горния десен панел лихвеният процент се повишава от самото начало и след това спада; след четири тримесечия той спада под 0 и след това се връща към устойчивото си състояние отдолу.
- В долния ляв панел е изобразена реакцията на производството; то се повишава при въздействието и след това монотонно спада до устойчивото си състояние.
- В долния среден панел е показан отговорът на самата технология. Тя също се повишава в момента на удара и след това монотонно спада до своето стабилно състояние.
Точните апостериорни средни стойности и достоверните интервали могат да бъдат разгледани с таблицата bayesirf. По-долу представяме в табличен вид реакцията на потреблението на технологичен шок.
. bayesirf table irf, impulse(z) response(c) Results from rbc_model
| (1) (2) (3) | ||
| step | irf Lower Upper | |
| 0 | .363699 .209593 .502829 | |
| 1 | .421867 .245335 .587063 | |
| 2 | .445802 .269215 .606835 | |
| 3 | .446962 .280481 .595064 | |
| 4 | .433453 .282893 .575041 | |
| 5 | .410962 .282863 .540024 | |
| 6 | .383436 .272859 .511974 | |
| 7 | .353574 .254899 .473345 | |
| 8 | .323189 .227486 .440766 | |
| 9 | .293459 .195011 .40683 | |
| 10 | .265119 .162333 .379442 | |
| 11 | .238595 .133143 .354938 | |
| 12 | .214099 .108564 .334151 | |
| 13 | .1917 .087822 .313609 | |
| 14 | .171372 .071785 .294301 | |
| 15 | .153031 .057275 .270277 | |
| 16 | .136556 .045631 .251522 | |
След технологичен шок с едно стандартно отклонение потреблението се повишава и достига връх от 0,447 % над стабилната си стойност през третия период след шока.
